7. Таблицы истинности. Булевы функции, принципы минимизации.

Как уже отмечалось, каждая из булевых переменных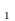 x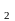 ,x , . . ., x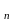 может принимать только два значения. Все точки внутри схемы и ее выходы также обладают этим свойством. Таблица, со­держащая все возможные комбинации значений входных переменных вместе с соответствующими им значениями выходных переменных, т. е. значениями функций, называется таблицей истинности (комбинационной таблицей).

Функции любого количества булевых переменных могут быть выражены через функции только двух переменных. Для этого пользуются подстановкой на место переменных других булевых функций, а также перестановкой переменных местами (перенумерация). Оба этих приема объединены общим названием – суперпозиция.

Функционально полный набор булевых функций, т. е. такой набор, через функции которого методом суперпозиции выражается любая булева функция двух переменных, может содержать всего одну функцию. К ней можно свести всю алгебру логики.

Наиболее важные функции, отражающие основные соотношения булевой алгебры, перечислены в табл. 4.1.

Первые три пары теорем, по существу, описывают свойства опе­раций И, ИЛИ, НЕ. Переменные в теоремах могут обозначать произвольные булевы выражения. Например, теорема 3а устанавливает, что операция ИЛИ над логической 1 в качестве одного операнда и чем угодно в качестве другого дает логическую 1.

Таблица 4.1. Теоремы булевой алгебры

№ п/п	Теорема	№ п/п	Теорема	Название (закон)
1а		1b
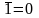
2а	x+0=x	2b
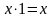
3а	x+1=1	3b
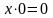
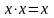
4а	x+x=x	4b		Идемпотентности
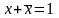
5а		5b
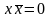
6а				Двойного отрицания
7а	x+y=y+x	7b	xy=yx	Коммутативности
8а	x+xy=x	8b	x(x+y)=x	Поглощения
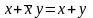
9а		9b
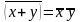
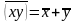
10а		10b		Де Моргана
11а	(x+y)+z=x+(y+z)=x+y+z	11b	(xy)z=x(yz)=xyz	Ассоциативности
12а	x+yz=(x+y)(x+z)	12b	x(y+z)=xy+xz	Дистрибутивности

Четвертая теорема, говорит о том, что повторяющиеся переменные в выражении излишни и их можно опустить. Таким образом, понятия возведения в степень и умножения на коэффициенты, отличные от логического 0 или логи­ческой 1 (т. е. числа), не имеют смысла в булевой алгебре. Закон двойного отрицания устанавливает, что дважды выполненное отрицание эквивалентно пустой операции.

В теоремах (7, 8, 9, 10) участвуют по две переменных. 7 – закон коммутативности – устанавливает перестановочность переменных в операции. Теоремы 8 и 9 полезны при упрощении булевых выражений. Теорема 10  –  закон де Моргана – описывает эффект взятия отрицания от пере­менных, связанных операциями И и ИЛИ.

В теоремах (11, 12) участвует по три переменных. Со­гласно закону ассоциативности, переменные можно группировать в любом порядке как для операции И, так и для операции ИЛИ. Закон дистрибутивности говорит о том, что в булевой алгебре допу­скается вынесение общего множителя за скобки.

Существует много способов использования выше приведенных теорем булевой алгебры, которые являются правилами преобразования булевых выражений. Новые выражения могут получиться проще или сложнее исходного в зависимости от целей преобразования.

Для минимизации переключательных функций используют два основных метода: метод Квайна и метод карт Карно (диаграмм Веча).

Чтобы исключить неточности при упрощении выражений используют диаграммы минимизации.

Диаграммы минимизации содержат 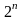клеточек, каждая из ко­торых предназначена для одной из простых конъюнкций или для одного набора значений переменных. В случае 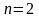диаграмма для минимизации совпадает с формой представления таблицы значений функции двух переменных.Этот же принцип сохраняется и при большем количестве переменных.

Для 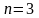диаграмма строится путем пририсовки к ней для двух переменных ее зеркального изображения (рис. 4.1).

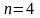
	0	1			00	01	11	10			00	01	11	10
0				0						00
1				1						01
										11
	0	1			00	01	11	10		10
0	00	01		0	000	001	011	010
1	10	11		1	100	101	111	110			00	01	11	10
										00	0	1	3	2
	0	1			00	01	11	10		01	4	5	7	6
0	0	1		0	0	1	3	2		11	12	13	15	14
1	2	3		1	4	5	7	6		10	8	9	11	10

Рис. 4.1. Диаграммы минимизации

Используя диаграммы, нет необходимости записывать булево выражение искомой комбинационной схемы. Достаточно лишь занести 1 в клеточки, соответствующие наборам переменных, при которых на выходе комбинационной схемы должен быть сиг­нал1.

Если занесенные единицы образуют прямоугольник из 2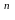 клето­чек, то логическая сумма соответствующих им простых конъюнк­ций может быть заменена укороченной конъюнкцией, содержащей лишь те переменные, значения которых одинаковы для всех клето­чек данного прямоугольника.

Искомое минимизированное булево выражение есть сумма конъюнкций контуров, охватываю­щих все без исключения единицы. При этом крайние правый и левый столбцы диаграммы и верхняя и нижняя ее строки считаются соседними, а контуры могут перекрываться.