14. Свойство непрерывных функций.

Теорема 1. Сумма непрерывных функций есть функция непрерывная.  Доказательство. Пусть функции     и     непрерывны в точке  a. Тогда

Согласно свойству пределов функций существование пределов функций     и     гарантирует существование предела их суммы. При этом

что и требовалось доказать.  Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.  Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная.  Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная.  Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.  Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.

Теорема 4. Любая элементарная функция непрерывна в области своего определения.  Для доказательства этой теоремы нужно показать, что для любого числа  a  из области определения элементарной функции     выполняется условие

Продемонстрируем справедливость теоремы на некоторых конкретных примерах.

1. Пусть 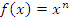  , где  n  – целое положительное число. Тогда

 

Первый член в правой части этого равенства представляет собой бесконечно малую функцию при  x → a  и, следовательно,

2. Покажем, что показательная функция 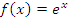   является непрерывной в каждой точке  a. Действительно,

   

Теорема 5. Пусть функция     непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка  c, в которой   .  Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами,     принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение. 

15. Точки разрыва первого и второго рода.

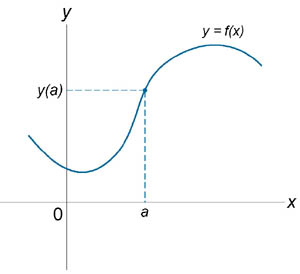
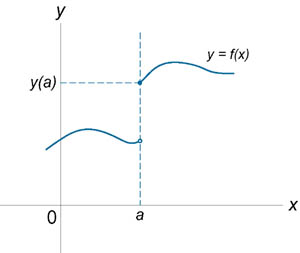
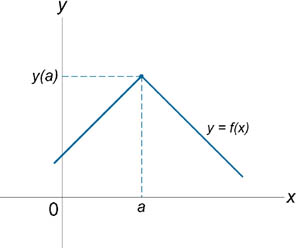
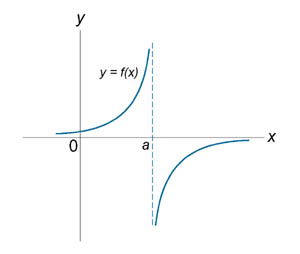
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.

Непрерывна при x = a.		Имеет разрыв при x = a.
Непрерывна при x = a.		Имеет разрыв при x = a.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел   и правосторонний предел  ;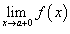

• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 

Пример этого маразма…..

Показать, что функция   имеет устранимый разрыв в точке x = 0.

Решение.

Очевидно, данная функция не определена при x = 0. Поскольку sin x является непрерывной функцией для всехx, то искомая функция   также непрерывна при всех x за исключением точки x = 0.  Так как 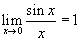 , то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию

      

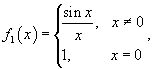
которая будет непрерывной при любом действительном x.