
- •2.Уравнение Бернули
- •3. Теорема Лейбница
- •1.Полный дифференциал функции нескольких переменных
- •3. Признак Даламбера сходимости знакоположительных рядов
- •1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •2.Методы интегрирования определенных интегралов
- •3. Знакопеременные ряды. Теорема об абсолютной сходимости
- •1.Производная функции по направлению
- •1. Вывод формулы Тейлора
- •2. Второй признак сравнения знакоположительных рядов
- •3. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница.Гамма-функция
- •2. Дифференциальные уравнения с разделяющимися переменными.
3. Признак Даламбера сходимости знакоположительных рядов
Если
для знакоположительного ряда
 существует предел отношения последующего
члена ряда к предыдущему при неограниченном
возрастании их номеров, т. е. существует
предел
существует предел отношения последующего
члена ряда к предыдущему при неограниченном
возрастании их номеров, т. е. существует
предел
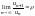 ,
то:если
<
1, то ряд сходится; 2) если
> 1, то ряд расходится;3) если
= 1, то данный признак не позволяет решить
вопрос о сходимости ряда (ряд может как
сходиться, так и расходиться).Д о к а з
а т е л ь с т в о.1. Пусть
,
то:если
<
1, то ряд сходится; 2) если
> 1, то ряд расходится;3) если
= 1, то данный признак не позволяет решить
вопрос о сходимости ряда (ряд может как
сходиться, так и расходиться).Д о к а з
а т е л ь с т в о.1. Пусть
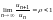 .
Если
< 1, то всегда найдется число q,
удовлетворяющее неравенству
< q
< 1. В этом случае по определению предела
существует такое число N,
что если номер члена ряда n
> N,
то отношение
.
Если
< 1, то всегда найдется число q,
удовлетворяющее неравенству
< q
< 1. В этом случае по определению предела
существует такое число N,
что если номер члена ряда n
> N,
то отношение
 меньше этого числа q,
т.е.
меньше этого числа q,
т.е.
 .
Данное неравенство представим в следующем
виде
.
Данное неравенство представим в следующем
виде
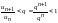 .
Отношение
.
Отношение
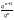 является отношением последующего члена
ряда к предыдущему для бесконечной
убывающей геометрической прогрессии
является отношением последующего члена
ряда к предыдущему для бесконечной
убывающей геометрической прогрессии
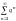 ,
которая сходится, так как знаменатель
прогрессии меньше единицы (q
<
1). В соответствии с теоремой 8.4 (третий
признак сравнения рядов) ряд
,
которая сходится, так как знаменатель
прогрессии меньше единицы (q
<
1). В соответствии с теоремой 8.4 (третий
признак сравнения рядов) ряд
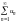 сходится.
сходится.
2.
Пусть
 .
Тогда существует такое число q,
которое больше единицы, но меньше ,
т. е.
.
Тогда существует такое число q,
которое больше единицы, но меньше ,
т. е.
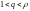 .
В этом случае существует такое число
N,
что если номер члена ряда n
> N,
то отношение
.
В этом случае существует такое число
N,
что если номер члена ряда n
> N,
то отношение
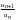 больше q,
т. е.
больше q,
т. е.
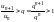 .
Тогда по теореме 8.4 ряд
.
Тогда по теореме 8.4 ряд
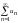 расходится.
расходится.
Данный признак Даламбера является наиболее простым и часто применяемым. Однако он дает ответ на вопрос о сходимости ряда только в тех случаях, когда ряд достаточно быстро сходится или расходится.
Билет 14.
1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
1.
Вычисление значений функций и их
приращений.Используем то, что полный
дифференциал является главной линейной
частью приращения функции (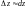 ).
Пусть известно значение функции
).
Пусть известно значение функции
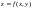 в некоторой точке
в некоторой точке
 и имеется точка
и имеется точка
 ,
находящейся в некоторой достаточно
малой окрестности точки
,
находящейся в некоторой достаточно
малой окрестности точки
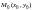 .
Можно найти приращение функции
.
Можно найти приращение функции
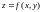 по формуле
по формуле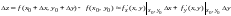 .Можно
найти также значение этой функции в
точке
.Можно
найти также значение этой функции в
точке
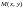 по формуле
по формуле
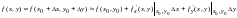 .Здесь
.Здесь
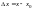 ,
,
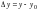
приращения независимых переменных,
приращения независимых переменных,
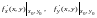
значения
частных производных функции в точке
.
значения
частных производных функции в точке
.
2.Методы интегрирования определенных интегралов
При
вычислении определенных интегралов
используются те же методы, что и при
нахождении неопределенных интегралов.
Однако, имеются некоторые особенности.1.
Замена переменной в определенном
интеграле отличается от замены переменной
в неопределенном интеграле тем, что в
результате замены изменяются пределы
интегрирования и нет необходимости
выполнять обратную замену. Пусть функция
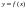 непрерывна на отрезке
непрерывна на отрезке
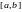 ,
функция
,
функция
 имеет непрерывную производную на
отрезке
имеет непрерывную производную на
отрезке
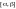 .
Тогда
.
Тогда
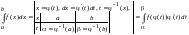 .
.
Пример
5.2. Найти
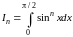 ,
где
,
где
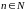 .
.
Используем
интегрирование по частям для нахождения
рекуррентной формулы для вычисления
интегралов вида
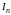 при любом n
N.
при любом n
N.
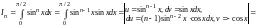
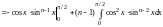 .
.
Учтем,
что
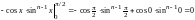 ,
получим
,
получим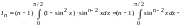
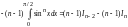 .Получили
уравнение относительно интеграла
:
.Получили
уравнение относительно интеграла
: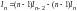 .
Отсюда получаем рекуррентную формулу
.
Отсюда получаем рекуррентную формулу
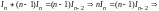
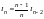 .
.
