
- •2.Уравнение Бернули
- •3. Теорема Лейбница
- •1.Полный дифференциал функции нескольких переменных
- •3. Признак Даламбера сходимости знакоположительных рядов
- •1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •2.Методы интегрирования определенных интегралов
- •3. Знакопеременные ряды. Теорема об абсолютной сходимости
- •1.Производная функции по направлению
- •1. Вывод формулы Тейлора
- •2. Второй признак сравнения знакоположительных рядов
- •3. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница.Гамма-функция
- •2. Дифференциальные уравнения с разделяющимися переменными.
1.Производная функции по направлению
Пусть
функция
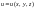 непрерывная и дифференцируемая, вектор
непрерывная и дифференцируемая, вектор
 задает направление. Пусть имеется точка
задает направление. Пусть имеется точка
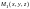 и в направлении
от нее точка
и в направлении
от нее точка
 рис. Вектор
рис. Вектор
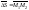 имеет координаты
имеет координаты
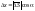 ,
,
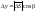 ,
,
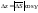 ,
т. е.
,
т. е.
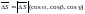 .
.
Модуль
вектора
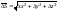 ,
,
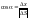 ,
,
 ,
,
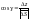 .
.
К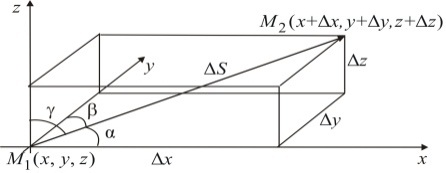 осинусы
cos,
cos,
cos
называются направляющими косинусами
вектора
.
Если вектор
единичный
осинусы
cos,
cos,
cos
называются направляющими косинусами
вектора
.
Если вектор
единичный
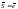 ,
то
,
то
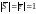 и его координатами являются направляющие
косинусы, т. е.
и его координатами являются направляющие
косинусы, т. е.
 .
Производной функции
.
Производной функции
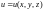 по направлению вектора
по направлению вектора
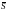 в точке
в точке
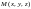 называется предел отношения приращения
функции в этом направлении к приращению
длины (модуля)
вектора
называется предел отношения приращения
функции в этом направлении к приращению
длины (модуля)
вектора
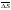 ,
при
,
при
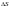 стремящемся к нулю
стремящемся к нулю
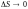 ,
т. е.
,
т. е.
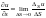 .
Находим
.
Находим
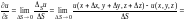
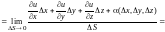
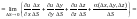
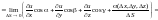
 .
Таким образом, получена формула
дифференцирования функции по направлению
вектора
.
Таким образом, получена формула
дифференцирования функции по направлению
вектора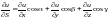 .
.
Градиент функции, его свойства
Градиентом
функции
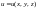 называется вектор
называется вектор
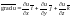 ,
где
,
где
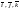
единичные векторы координатного базиса
в прямоугольной декартовой системе
координат. Кратко можно записать
единичные векторы координатного базиса
в прямоугольной декартовой системе
координат. Кратко можно записать
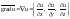 .
Здесь
знак набла. Теорема
3.5.
Производная функции
.
Здесь
знак набла. Теорема
3.5.
Производная функции
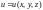 по направлению вектора
по направлению вектора
 равняется проекции градиента этой
функции на это направление, т. е.
равняется проекции градиента этой
функции на это направление, т. е.
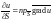 .
Известно, что проекция некоторого
вектора
.
Известно, что проекция некоторого
вектора
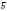 на направление вектора
на направление вектора
 равняется
равняется
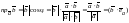 .
.
Здесь
угол между векторами
 и
и
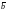 ,
,
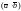
скалярное произведение векторов,
скалярное произведение векторов,
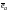
единичный вектор, совпадающий по
направлению с вектором
.
единичный вектор, совпадающий по
направлению с вектором
.
Найдем
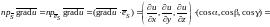 .
.

Свойство
1.
Производная функции
 по направлению вектора
по направлению вектора
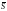 достигает своего наибольшего значения,
если направление вектора
достигает своего наибольшего значения,
если направление вектора
 совпадает с направлением градиента
этой функции. Действительно, производную
данной функции по направлению вектора
можно записать следующим образом
совпадает с направлением градиента
этой функции. Действительно, производную
данной функции по направлению вектора
можно записать следующим образом
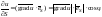 ,
где
угол между градиентом и вектором
.
Если этот угол равен нулю
= 0 , то косинус этого угла и производная
функции принимают наибольшие значения,
cos0
= 1,
,
где
угол между градиентом и вектором
.
Если этот угол равен нулю
= 0 , то косинус этого угла и производная
функции принимают наибольшие значения,
cos0
= 1,
 .
Свойство
2.
Производная функции
.
Свойство
2.
Производная функции
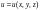 по направлению вектора
равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции. Действительно,
по направлению вектора
равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции. Действительно,
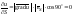 .
Данные свойства используются при решении
задач оптимизации (нахождения наибольшего,
наименьшего значений функций) с помощью
численных методов. Градиент функции
определяет направление наибольшего
изменения функции. Направление
перпендикулярное градиенту определяет
направление, в котором функция не
изменяется. Известно, что на поверхности
уровня
.
Данные свойства используются при решении
задач оптимизации (нахождения наибольшего,
наименьшего значений функций) с помощью
численных методов. Градиент функции
определяет направление наибольшего
изменения функции. Направление
перпендикулярное градиенту определяет
направление, в котором функция не
изменяется. Известно, что на поверхности
уровня
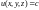 функция
функция
 не изменяется. Следовательно, градиент
функции перпендикулярен поверхности
уровня. Это обстоятельство можно
использовать для написания уравнения
касательной плоскости к поверхности
не изменяется. Следовательно, градиент
функции перпендикулярен поверхности
уровня. Это обстоятельство можно
использовать для написания уравнения
касательной плоскости к поверхности
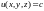 .
Пусть точка
.
Пусть точка
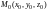 принадлежит поверхности. Найдем градиент
функции
принадлежит поверхности. Найдем градиент
функции
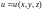 в этой точке
в этой точке
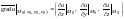 и напишем уравнение плоскости, проходящей
через точку
и напишем уравнение плоскости, проходящей
через точку
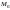 перпендикулярно вектору
перпендикулярно вектору
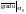 .
Получаем уравнение касательной плоскости
.
Получаем уравнение касательной плоскости
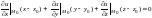 .
.
2.
Общее
решение линейного однородного
дифференциального уравнения n-ого
порядка с постоянными коэффициентами.
Общее
решение неоднородного уравнения, как
было показано ранее (теорема 7.4),
находится как сумма
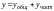 общего решения
общего решения
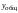 однородного уравнения и частного
решения
однородного уравнения и частного
решения
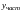 неоднородного уравнения, т. е.
неоднородного уравнения, т. е.
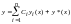 ,
где
,
где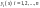
линейно независимые решения однородного
уравнения;
линейно независимые решения однородного
уравнения;
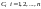 произвольные
постоянные;
произвольные
постоянные;
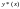
частное решение исходного неоднородного
уравнения. В общем случае линейное
однородное дифференциальное уравнение
n-го
порядка имеет вид
частное решение исходного неоднородного
уравнения. В общем случае линейное
однородное дифференциальное уравнение
n-го
порядка имеет вид
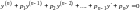 ,
где
,
где
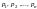
постоянные величины. Частные решения
однородного уравнения ищут в виде
постоянные величины. Частные решения
однородного уравнения ищут в виде
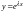 .
Производные этой функции равны
.
Производные этой функции равны
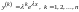 .
Подставляем функцию
.
Подставляем функцию
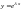 и ее производные в однородное уравнение
и ее производные в однородное уравнение
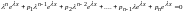 .
Делим это уравнение на
.
Делим это уравнение на
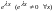 ,
получаем уравнение
,
получаем уравнение
 .
Данное уравнение называется
характеристическим.
Характеристическое уравнение является
алгебраическим уравнением n-ой
степени относительно .
Любое алгебраическое уравнение n-ой
степени имеет в комплексной плоскости
n
корней. Рассмотрим все возможные случаи
решения однородного дифференциального
уравнения в зависимости от вида корней
его характеристического уравнения.
Случай
1.
Все корни характеристического уравнения
.
Данное уравнение называется
характеристическим.
Характеристическое уравнение является
алгебраическим уравнением n-ой
степени относительно .
Любое алгебраическое уравнение n-ой
степени имеет в комплексной плоскости
n
корней. Рассмотрим все возможные случаи
решения однородного дифференциального
уравнения в зависимости от вида корней
его характеристического уравнения.
Случай
1.
Все корни характеристического уравнения
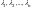 вещественные различные. В этом случае
дифференциальное уравнение имеет n
линейно независимых частных решений
вещественные различные. В этом случае
дифференциальное уравнение имеет n
линейно независимых частных решений
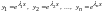 .
Общее решение однородного уравнения
имеет вид
.
Общее решение однородного уравнения
имеет вид
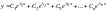 или
или
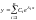 ,
где
,
где

произвольные постоянные. Случай
2.
Характеристическое уравнение имеет
пару комплексно-сопряженных корней
произвольные постоянные. Случай
2.
Характеристическое уравнение имеет
пару комплексно-сопряженных корней
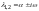 ,
где
,
где
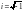 .
Тогда этим корням соответствует два
линейно независимых комплексно-сопряженных
решения
.
Тогда этим корням соответствует два
линейно независимых комплексно-сопряженных
решения
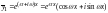 ,
,
 .
Из этих решений составляют два линейно
независимых действительных решения
.
Из этих решений составляют два линейно
независимых действительных решения
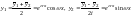 .
Общее решение однородного дифференциального
уравнения имеет вид
.
Общее решение однородного дифференциального
уравнения имеет вид
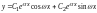 или
или
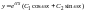 .
Случай
3.
Характеристическое уравнение имеет
действительный корень
кратности k.
Тогда ему соответствует
k
линейно независимых частных решения
однородного уравнения, которые имеют
вид
.
Случай
3.
Характеристическое уравнение имеет
действительный корень
кратности k.
Тогда ему соответствует
k
линейно независимых частных решения
однородного уравнения, которые имеют
вид
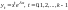 .
Общее решение однородного дифференциального
уравнения имеет вид
.
Общее решение однородного дифференциального
уравнения имеет вид
 .
Случай
4.
Характеристическое уравнение имеет
пару комплексно-сопряженных корней
кратности k.
Тогда этим корням соответствует 2k
линейно независимых частных решений
однородного уравнения, которые имеют
вид
.
Случай
4.
Характеристическое уравнение имеет
пару комплексно-сопряженных корней
кратности k.
Тогда этим корням соответствует 2k
линейно независимых частных решений
однородного уравнения, которые имеют
вид
 .
Общее решение однородного дифференциального
уравнения имеет вид
.
Общее решение однородного дифференциального
уравнения имеет вид

Или
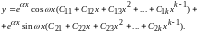
3.
Интегральный признак Коши.
Если
члены знакоположительного ряда
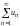 ,
являющиеся значениями функции
целочисленного аргумента
,
являющиеся значениями функции
целочисленного аргумента
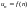 ,
монотонно убывают и стремятся к нулю
,
монотонно убывают и стремятся к нулю
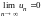 ,
то: 1) если
,
то: 1) если
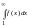 сходится, то и ряд
сходится, то и ряд
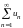 сходится; 2) если
сходится; 2) если
 расходится, то и ряд
расходится, то и ряд
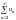 расходится. Д о к о з а т е л ь с т в о. В
прямоугольной декартовой системе
координат
расходится. Д о к о з а т е л ь с т в о. В
прямоугольной декартовой системе
координат
 непрерывная кривая
непрерывная кривая
 проходит через точки
проходит через точки
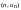 и ограничивает сверху криволинейную
трапецию ABCD
(рис. 86). Площадь этой криволинейной
трапеции равняется
и ограничивает сверху криволинейную
трапецию ABCD
(рис. 86). Площадь этой криволинейной
трапеции равняется
 .
Построим две ступенчатые фигуры с
угловыми точками
.
Построим две ступенчатые фигуры с
угловыми точками

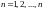 .
Эти ступенчатые фигуры состоят из
прямоугольников, основания которых
равняются единице, а высоты значениям
.
Эти ступенчатые фигуры состоят из
прямоугольников, основания которых
равняются единице, а высоты значениям
 .
Найдем площади этих фигур.
.
Найдем площади этих фигур.
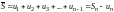 ,
,
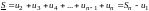 ,
,
где

n-я
частичная сумма ряда. Площади этих
ступенчатых фигур ограничивают площадь
криволинейной трапеции ABCD
снизу и сверху
n-я
частичная сумма ряда. Площади этих
ступенчатых фигур ограничивают площадь
криволинейной трапеции ABCD
снизу и сверху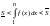
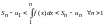 .
.
Р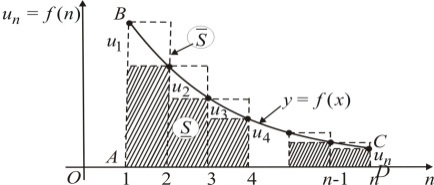 ассмотрим
левую часть этого неравенства
ассмотрим
левую часть этого неравенства
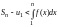
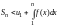 .
.
При
неограниченном возрастании числа n
членов ряда частичные суммы ряда
монотонно возрастают, так как ряд
знакоположительный. При этом интеграл
 также возрастает и ограничен величиной
интеграла
также возрастает и ограничен величиной
интеграла
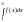 .
Поэтому
.
Поэтому
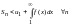 ,
т. е. последовательность частичных сумм
ограничена. По теореме Вейерштрасса
существует предел
,
т. е. последовательность частичных сумм
ограничена. По теореме Вейерштрасса
существует предел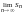 .
Следовательно, ряд сходится. Рассмотрим
правую часть неравенства
.
Следовательно, ряд сходится. Рассмотрим
правую часть неравенства
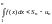
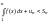 .
По условию теоремы
.
По условию теоремы
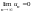 .
Если
.
Если
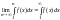 неограниченно возрастает, то и предел
частичных сумм
неограниченно возрастает, то и предел
частичных сумм
 неограниченно возрастает и, следовательно,
ряд расходится. Таким образом, интегральный
признак Коши в принципе позволяет для
любого ряда решить вопрос о его сходимости.
Трудность в его применении заключается
в нахождении несобственных интегралов.
Возможности в их нахождении ограниченные.
неограниченно возрастает и, следовательно,
ряд расходится. Таким образом, интегральный
признак Коши в принципе позволяет для
любого ряда решить вопрос о его сходимости.
Трудность в его применении заключается
в нахождении несобственных интегралов.
Возможности в их нахождении ограниченные.
Билет 17.
1.Теорема
Лагранжа
о
конечном приращении функции.
Если функция
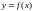 непрерывна на отрезке
непрерывна на отрезке
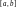 и дифференцируемая в каждой его внутренней
точке, то на интервале (a,
b)
найдется такая точка х
= с,
что
и дифференцируемая в каждой его внутренней
точке, то на интервале (a,
b)
найдется такая точка х
= с,
что
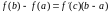 .
.
Геометрический смысл теоремы Лагранжа
На
основании формулы
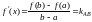 можно утверждать следующее.
можно утверждать следующее.
|
Если
график функции y
= f(x)
непрерывный на отрезке
|
2. Частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами. Вид частного решения неоднородного дифференциального уравнения
 зависит
от вида правой части этого уравнения
(функции
зависит
от вида правой части этого уравнения
(функции
 )
и от величин корней характеристического
уравнения. Рассмотрим нахождение
частного решения для двух видов функции
.
Случай
1.
Правая часть уравнения
)
и от величин корней характеристического
уравнения. Рассмотрим нахождение
частного решения для двух видов функции
.
Случай
1.
Правая часть уравнения
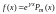 ,
где
вещественное значение,
,
где
вещественное значение,
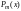
многочлен m-й
степени. В этом случае частное решение
уравнения ищется в виде
многочлен m-й
степени. В этом случае частное решение
уравнения ищется в виде
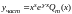 ,где
,где
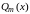
многочлен m-й
степени, s
степень кратности корня характеристического
уравнения
многочлен m-й
степени, s
степень кратности корня характеристического
уравнения
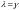 .
Если
.
Если
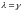 не является корнем характеристического
уравнения, то s
= 0. Случай
2.
Правая часть неоднородного дифференциального
уравнения имеет вид
не является корнем характеристического
уравнения, то s
= 0. Случай
2.
Правая часть неоднородного дифференциального
уравнения имеет вид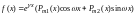 ,
где
и
вещественные значения,
,
где
и
вещественные значения,
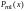 и
и
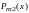
многочлены степени
многочлены степени
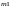 и
и
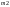 соответственно. В этом случае частное
решение дифференциального уравнения
ищется в виде
соответственно. В этом случае частное
решение дифференциального уравнения
ищется в виде
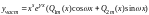 ,
,
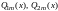
многочлены степени
многочлены степени
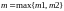 ,
s
кратность корня характеристического
уравнения
,
s
кратность корня характеристического
уравнения
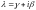 ,
где
,
где
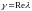 совпадает с числом
в показателе степени
совпадает с числом
в показателе степени
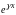 в функции
в функции
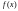 правой части уравнения. Если
в
не совпадает с
правой части уравнения. Если
в
не совпадает с
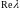 ,
то s
= 0.
,
то s
= 0.
3.
. Знакочередующиеся ряды. Теорема
Лейбниц.
Если
члены знакочередующегося ряда
 монотонно
убывают
монотонно
убывают
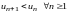 и стремятся к нулю
и стремятся к нулю
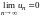 ,
то ряд сходится; причем сумма ряда по
абсолютной величине не превосходит
первого члена ряда
,
то ряд сходится; причем сумма ряда по
абсолютной величине не превосходит
первого члена ряда
 .
.
Д
о к а з а т е л ь с т в о. По определению
знакочередующегося ряда
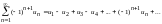 предполагается,
что члены ряда положительные
предполагается,
что члены ряда положительные
 .
Рассмотрим две частичные суммы ряда: с
четным числом членов ряда
.
Рассмотрим две частичные суммы ряда: с
четным числом членов ряда
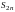 и с нечетным числом членов
и с нечетным числом членов
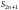 .
В сумме с четным числом членов
.
В сумме с четным числом членов
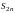 сначала сгруппируем члены попарно
следующим образом
сначала сгруппируем члены попарно
следующим образом
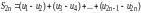 .
Так как члены ряда монотонно убывают
(
.
Так как члены ряда монотонно убывают
(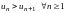 ),
то разность в каждой скобке суммы
),
то разность в каждой скобке суммы
 больше нуля и эта сумма монотонно
возрастает с увеличением числа членов
2n.
Теперь сгруппируем члены этой суммы
следующим образом
больше нуля и эта сумма монотонно
возрастает с увеличением числа членов
2n.
Теперь сгруппируем члены этой суммы
следующим образом
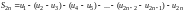 .
Так как в этой сумме также разность в
каждой скобке больше нуля, то сумма
монотонно убывает с увеличением числа
членов 2n
и не превосходит первого члена ряда
.
Следовательно, последовательность
частичных сумм ряда с четным числом
членов монотонно возрастает и ограничена.
Поэтому по теореме Вейерштрасса она
имеет некоторый предел
.
Так как в этой сумме также разность в
каждой скобке больше нуля, то сумма
монотонно убывает с увеличением числа
членов 2n
и не превосходит первого члена ряда
.
Следовательно, последовательность
частичных сумм ряда с четным числом
членов монотонно возрастает и ограничена.
Поэтому по теореме Вейерштрасса она
имеет некоторый предел
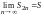 .
Найдем также предел частичных сумм ряда
с нечетным числом членов.
.
Найдем также предел частичных сумм ряда
с нечетным числом членов.
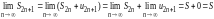 .
При нечетном числе членов ряда сумма
также не превосходит первого члена ряда
.
.
При нечетном числе членов ряда сумма
также не превосходит первого члена ряда
.
 .
Таким образом, предел частичных сумм
знакочередующегося ряда существует,
т. е. ряд всегда сходится, если его члены
монотонно убывают и стремятся к нулю.
Частичные суммы знакочередующегося
ряда меньше первого члена ряда
.
Таким образом, предел частичных сумм
знакочередующегося ряда существует,
т. е. ряд всегда сходится, если его члены
монотонно убывают и стремятся к нулю.
Частичные суммы знакочередующегося
ряда меньше первого члена ряда
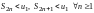 .
Члены ряда стремятся к нулю
.
Члены ряда стремятся к нулю
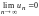 ,
поэтому сумма ряда не может превосходить
первого члена ряда
.
,
поэтому сумма ряда не может превосходить
первого члена ряда
.
Билет 18.

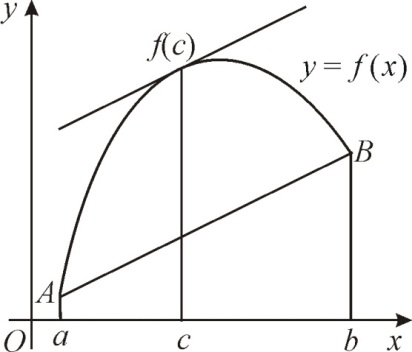
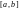 и гладкий на интервале
и гладкий на интервале
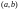 ,
то на этом интервале найдется такая
точка
,
то на этом интервале найдется такая
точка
 ,
в которой касательная параллельна
хорде, стягивающей граничные точки
графика функции (рис. 28).
,
в которой касательная параллельна
хорде, стягивающей граничные точки
графика функции (рис. 28).