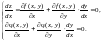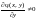- •2.Уравнение Бернули
- •3. Теорема Лейбница
- •1.Полный дифференциал функции нескольких переменных
- •3. Признак Даламбера сходимости знакоположительных рядов
- •1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •2.Методы интегрирования определенных интегралов
- •3. Знакопеременные ряды. Теорема об абсолютной сходимости
- •1.Производная функции по направлению
- •1. Вывод формулы Тейлора
- •2. Второй признак сравнения знакоположительных рядов
- •3. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница.Гамма-функция
- •2. Дифференциальные уравнения с разделяющимися переменными.
1. Вывод формулы Тейлора
Теорема. Если в некоторой окрестности точки х = а функция имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула
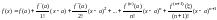 ,
,
где
 .
.
Доказательство. Используем теорему Ролля.
Обозначим
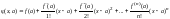 .
Покажем, что разность
.
Покажем, что разность
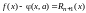 ,
где
,
где
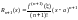 .
.
Для
этого составим вспомогательную функцию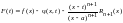
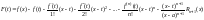
Найдем
значения функции
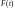 в граничных точках отрезка
в граничных точках отрезка
 .
.
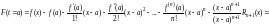
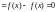 .
.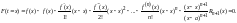
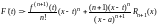 .
.
Найдем
значение производной в точке t
=
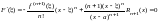 .
.
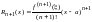 .
.
выражение
для
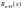 называется остаточным членом в форме
Лагранжа. Если представить
в виде
называется остаточным членом в форме
Лагранжа. Если представить
в виде
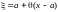 ,
где
,
где
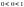 ,
то остаточный член примет вид
,
то остаточный член примет вид
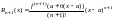 .
.
В
частном случае, если
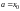 ,
,
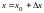 ,
то формула Тейлора примет вид
,
то формула Тейлора примет вид
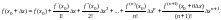
2. Второй признак сравнения знакоположительных рядов
Теорема.
Если отличен от нуля конечный предел
отношения соответствующих членов двух
знакоположительных рядов
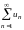 и
и
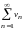 ,
т. е.
,
т. е.
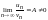 ,
то данные ряды сходятся или расходятся
одновременно.
,
то данные ряды сходятся или расходятся
одновременно.
Доказательство. По определению предела по Коши на языке - существование предела отношения членов рядов означает:
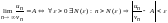 .
для любого n
>
N()
справедливы неравенства
.
для любого n
>
N()
справедливы неравенства
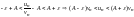 .
.
n
=1. т. е.
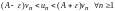 .
.
Тогда для частичных сумм рядов можно записать
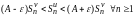 ,
где
,
где
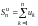 ,
,
 ..
..
1.
Ряд
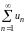 сходится.
сходится.
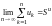 .
.
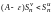 ,
можно записать
,
можно записать
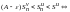
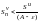 ,
,
т.
е. последовательность частичных сумм
ряда
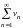 ,являющаяся
монотонно возрастающей, ограничена,
ряд сходится.
,являющаяся
монотонно возрастающей, ограничена,
ряд сходится.
2.
Ряд
расходится, т. е.
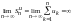 .
Тогда:
.
Тогда:
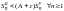 .
Отсюда - предел частичных сумм второго
ряда также неограничен
.
Отсюда - предел частичных сумм второго
ряда также неограничен
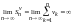 .
Следовательно, ряд
.
Следовательно, ряд
 расходится.
расходится.
3. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница.Гамма-функция
Пусть
в определенном интеграле пределы
интегрирования и подынтегральная
функция зависят от некоторого параметра
,
т.е. интеграл имеет вид
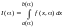 .
Требуется найти производную интеграла
.
Требуется найти производную интеграла
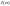 по этому параметру .
Будем считать, что функции
по этому параметру .
Будем считать, что функции
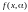 ,
,
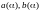 - дифференцируемые функции по .
Рассмотрим отдельно три случая, когда
в интеграле зависят от параметра либо
подынтегральная функция, либо какой-то
из пределов интегрирования. 1. Пусть
- дифференцируемые функции по .
Рассмотрим отдельно три случая, когда
в интеграле зависят от параметра либо
подынтегральная функция, либо какой-то
из пределов интегрирования. 1. Пусть
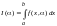 .
Найдем
.
Найдем
 Используем
теорему Лагранжа о конечном приращении
функции, запишем
Используем
теорему Лагранжа о конечном приращении
функции, запишем
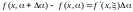 ,
где
,
где
 .
Тогда
.
Тогда
 .
Следовательно,
.
Следовательно,
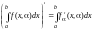 .
1.Пусть от параметра зависит верхний
предел интегрирования, т. е.
.
1.Пусть от параметра зависит верхний
предел интегрирования, т. е.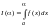 .
Найдем
.
Найдем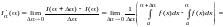
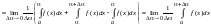 .По
теореме о среднем
.По
теореме о среднем
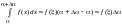 ,
где
,
где
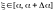 .Тогда
.Тогда
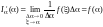 .
Следовательно,
.
Следовательно,
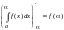
Если
верхний предел интегрирования сложная
функция
 ,
то производная интеграла найдется как
производная сложной функции, т. е.
,
то производная интеграла найдется как
производная сложной функции, т. е.
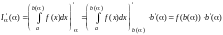 В
практических задачах нередко требуется
найти производную по x
от интеграла
В
практических задачах нередко требуется
найти производную по x
от интеграла
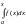 .
В этом интеграле x
под интегралом – это переменная
интегрирования, а верхний предел x
является
фактически параметром. Поэтому
.
В этом интеграле x
под интегралом – это переменная
интегрирования, а верхний предел x
является
фактически параметром. Поэтому
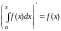 .3.
Если от параметра зависит только нижний
предел интегрирования, то переставим
верхний и нижний предел интегрирования
и получим
.3.
Если от параметра зависит только нижний
предел интегрирования, то переставим
верхний и нижний предел интегрирования
и получим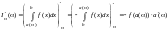 Используем
формулы дифференцирования сложной
функции нескольких переменных, получим
производную интеграла, зависящего от
параметра в общем случае
Используем
формулы дифференцирования сложной
функции нескольких переменных, получим
производную интеграла, зависящего от
параметра в общем случае
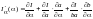 или
или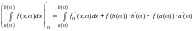 Данная
формула называется формулой Лейбница.
Данная
формула называется формулой Лейбница.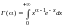 Данный
интеграл называется гамма-функцией. Он
часто используется в математической
статистике и других прикладных разделах
высшей математики. Найдем
Данный
интеграл называется гамма-функцией. Он
часто используется в математической
статистике и других прикладных разделах
высшей математики. Найдем
 .При
.При
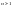 применим интегрирование по частям.
Получим
применим интегрирование по частям.
Получим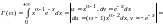
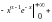
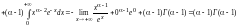 так
как
так
как
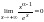 .
Таким образом
.
Таким образом
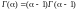 .
Получим формулу для нахождения
.
Получим формулу для нахождения
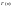 при n
целом. Так .как.
при n
целом. Так .как.
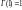 ,
то
,
то
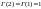 ,
,
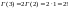 ,
,
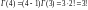 и т. д.
и т. д.

Билет 19.
1.
Условный экстремум функции нескольких
переменных. Метод множителей Лагранжа.
Найти
экстремум функции
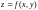 ,x
и y
удовлетворяют
уравнению
,x
и y
удовлетворяют
уравнению
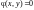 .
.
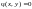 задает неявно функцию
задает неявно функцию
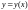 ,
подставим в ф-цию z,
,
подставим в ф-цию z,
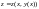 .
Находим критические точки (в них
производная = 0).
.
Находим критические точки (в них
производная = 0).
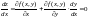 ,
,
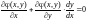 .
Решаем систему:
.
Решаем систему:
|
|
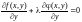 ,
,
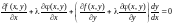 ,
следовательно
,
следовательно
 ,
решаем систему вместе с
,
решаем систему вместе с
 ,
что образует систему уравнений для
нахождения критических точек, которые
надо проверить на наличие в них экстремума
(достаточный признак). Метод
множителей Лагранжа. Левые
части уравнения – частые производные
ф-ции:
,
что образует систему уравнений для
нахождения критических точек, которые
надо проверить на наличие в них экстремума
(достаточный признак). Метод
множителей Лагранжа. Левые
части уравнения – частые производные
ф-ции:
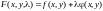 (ф-ция
Лагранжа). Система для нахождения
крит.т.:
(ф-ция
Лагранжа). Система для нахождения
крит.т.:
 ,
,
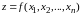 (в случае n переменных):
(в случае n переменных):
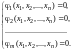
Ф-ция
Лагранжа:
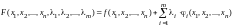 .
.
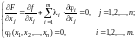 ,
крит.
Т.
,
крит.
Т.
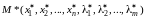 .
.