8.2. Инвариантность уравнений Максвелла относительно преобразований Лоренца

Как известно, механические явления в различных системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, протекают одинаково. С помощью механических измерений невозможно установить, какая из этих систем покоится, а какие – движутся, и поэтому можно лишь говорить об относительном движении этих систем друг по отношению к другу (принцип относительности для механических явлений).

Рассматривая поведение электрических, магнитных и электромагнитных полей при переходе от одной инерциальной системы в другую, было установлено, что с помощью электромагнитных явлений также нельзя установить существование абсолютного движения и поэтому нельзя обнаружить привилегированную систему отсчета. Все инерциальные системы отсчета равноправны между собой и во всех этих системах законы электромагнитных явлений одинаковы. В этом заключается физическая сущность принципа относительности для электромагнитных явлений.

Таким образом, существует одно абсолютное понятие – "единое электромагнитное поле", а его разделение на электрическую и магнитную составляющие является относительным и зависит от системы отсчета, которую выбирают для описания электромагнитных процессов. Это означает, что основная система уравнений электродинамики – система уравнений Максвелла – Лоренца – должна быть инвариантной. Ранее было показано, что система уравнений Максвелла в дифференциальной форме имеет вид

1)

2)

3)

4) (8.32)

В этой системе векторы E, H, B, D представляют собой характеристики электрического и магнитного полей,  - объемная плотность заряда и - вектор плотности электрического тока, связанный с объемной плотностью заряда соотношением

,

где - скорость движения заряда.

При этом и отличны от нуля только в тех областях пространства, которые заняты зарядами. В проекциях на оси координат неподвижной системы отсчета система уравнений имеет вид

1)

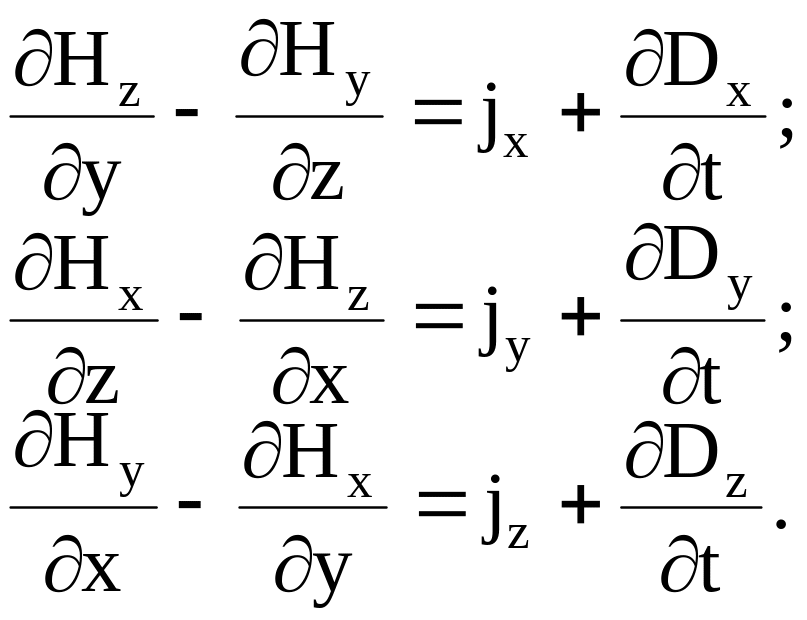
2)

3)

4) . (8.33)

При переходе из одной системы отсчета в другую проекции векторов электромагнитного поля E, H, B, D связаны между собой соотношениями

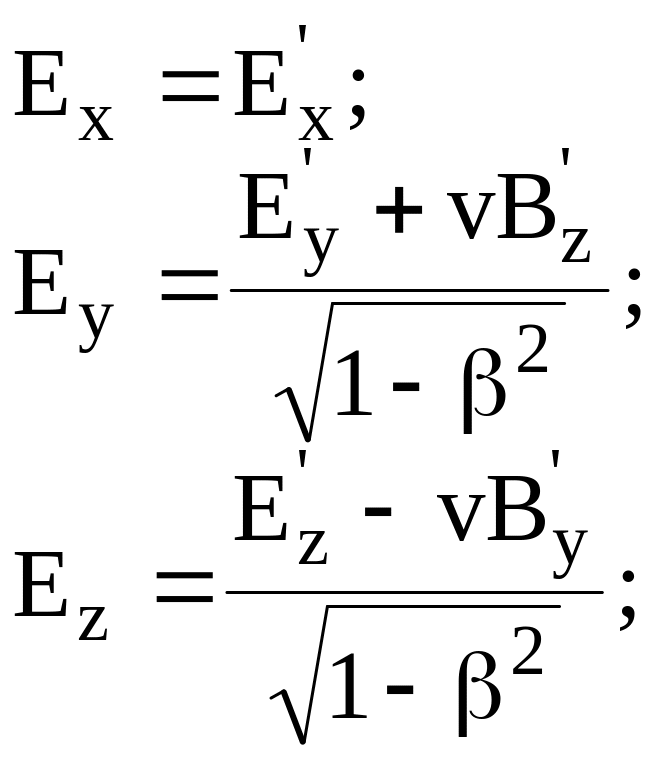
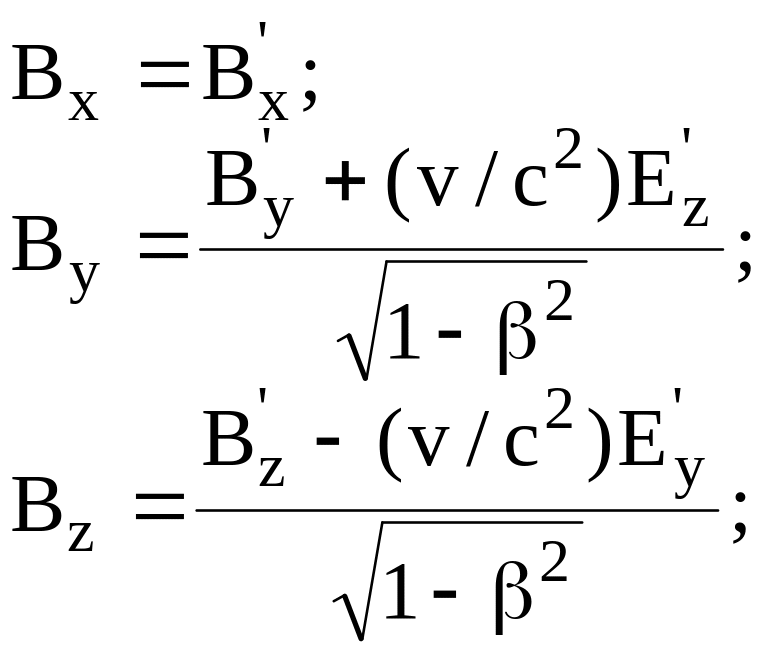(8.34)

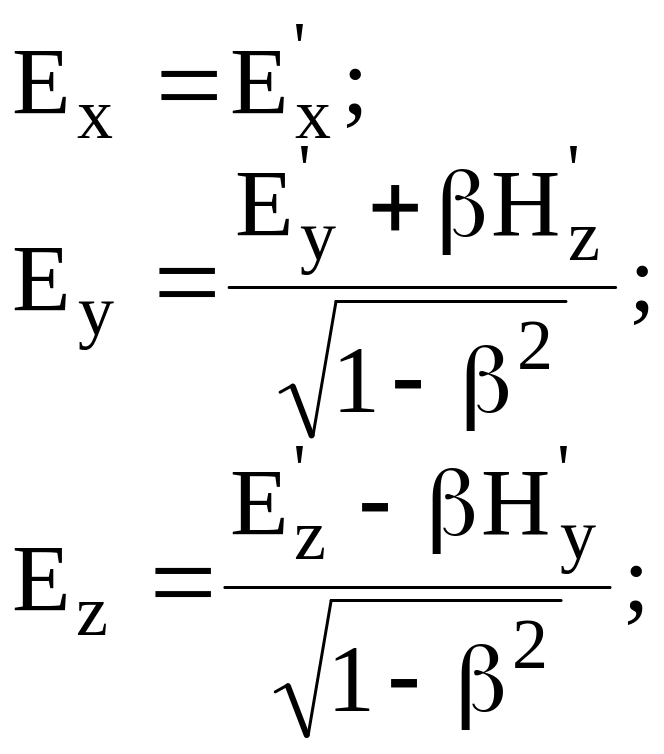
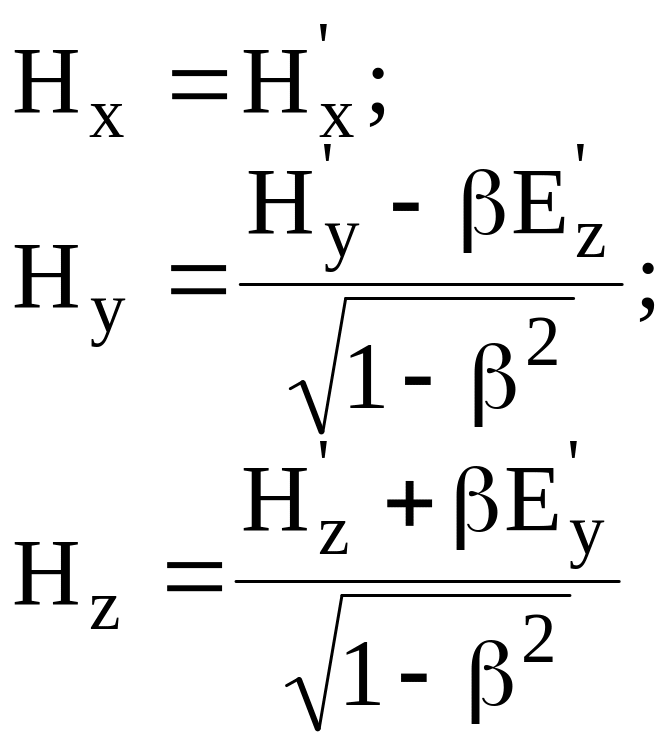(8.35)

или

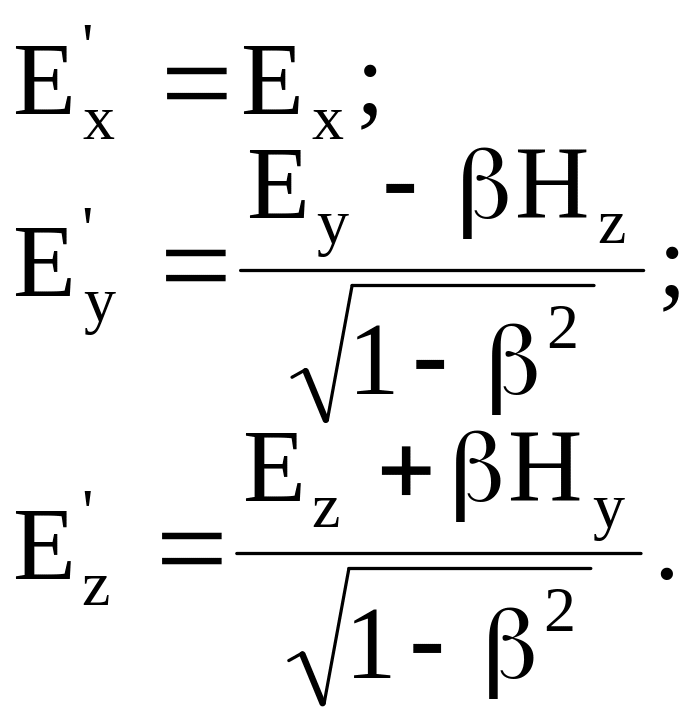
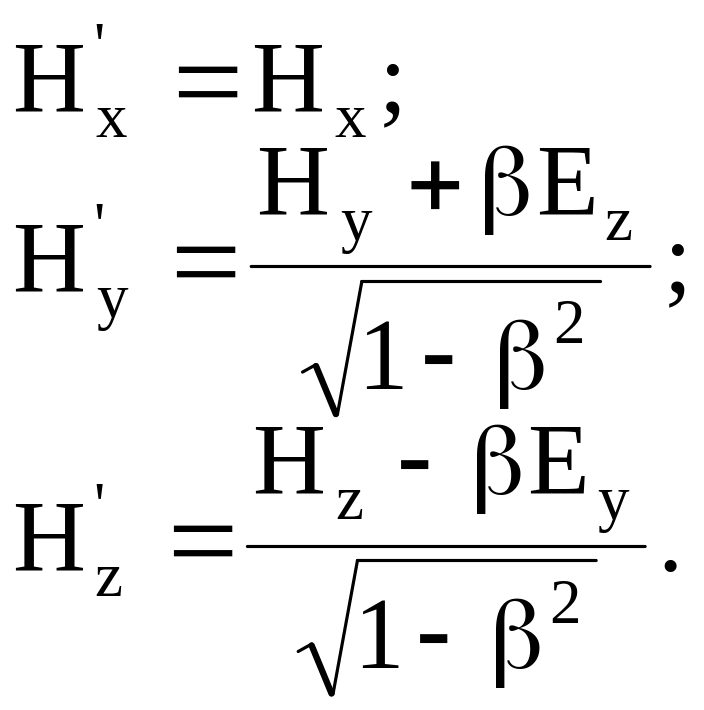(8.36)

Однако так как в векторной форме при , а одно из уравнений (8.36), например, имеет вид

,

то можно утверждать, что уравнения Максвелла в векторной форме не меняют своей формы при переходе от одной инерциальной системы отсчета к другой инерциальной системе отсчета, т.е. они инвариантны.

Лекция 9. Квазистационарное электромагнитное поле. Квазистационарные электрические токи

Квазистационарное электромагнитное поле. Квазистационарные электрические токи. Работа и мощность переменного электрического тока. Емкостное и индуктивное сопротивления цепи переменному току. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи. Вихревые электрические токи (токи Фуко). Скин-эффект.

9.1. Квазистационарное электромагнитное поле

При изучении переменных полей и токов необходимо принять во внимание два фактора:

1) конечную скорость распространения электромагнитных полей;

2) порождение магнитного поля, изменяющимся электрическим полем.

При не очень большой частоте переменного тока этими факторами можно пренебречь, т.е. считать, что электромагнитные поля распространяются в пространстве мгновенно, а токи смещения не существуют или магнитное поле порождается только токами проводимости. Токи и поля, удовлетворяющие этим условиям, называются квазистационарными.

Математически квазистационарность электромагнитных полей можно установить из следующих соображений.

Пусть имеется электромагнитное поле (периодический процесс), распространяющееся от источника со скоростью v. Тогда длина волны этого процесса, т.е. расстояние, на которое распространится электромагнитное поле за время, равное одному периоду T, равна

.

Пренебречь пространственным изменением некоторой величины, характеризующей процесс, можно только в том случае, если она рассматривается в областях, линейные размеры которых много меньше длины волны:

. (9.1)

Полученное соотношение (9.1) и является одним из условий квазистационарности электромагнитных полей (критерием пренебрежения конечной скоростью распространения этих полей).

Условие квазистационарности электромагнитных полей, возможно, в том случае, когда поля возникают в результате движения системы зарядов, совершающих медленное, квазистационарное (как бы стационарное) движение. В этом случае в уравнениях Максвелла производные от векторов и по времени малы по сравнению с пространственными производными, что несколько изменяет вид самих уравнений.

Медленное движение заряженных частиц предполагает их движение со скоростью , значительно меньшей по сравнению со скоростью распространения света в вакууме, которая является скоростью распространения всех электромагнитных взаимодействий. В этом случае можно приближенно считать, что поле в каждый момент времени определяется мгновенным расположением электрических зарядов. Кроме того, движущиеся заряды не могут покинуть пределы некоторой ограниченной области пространства.

Поскольку частицы (электрические заряды) не могут выйти за границы области, на ограничивающей ее поверхности должно выполняться условие

,

где - нормальная составляющая вектора плотности тока к поверхности.

При медленном движении зарядов изменение объемной плотности зарядов мало, следовательно

.

Это означает, что уравнение непрерывности будет иметь вид

.

Таким образом, при квазистационарном движении зарядов вектор плотности тока имеет соленоидальный характер, что позволяет представить их траектории движения в виде некоторых замкнутых трубок или нитей.

Для каждой замкнутой трубки с током, при условии совпадения направлений векторов и , можно записать

, (9.2)

где - сечение трубки;

- величина постоянного тока;

- элемент длины трубки с током.

Проинтегрировав соотношение (9.2) по всему объему, получим

, (9.3)

так как .

Смысл равенства (9.3) заключается в том, что в квазистационарном состоянии полный ток через любое сечение трубки равен нулю, т.е. число зарядов, проходящих по нормали к сечению через все трубки с током в обоих направлениях, должно быть одинаковым, поскольку заряды совершают движение в ограниченном объеме пространства.

С учетом данных замечаний можно установить систему уравнений Максвелла для такого движения электрических зарядов, оценить (по порядку величины) входящие в них величины.

Для оценки порядка величины производных по времени, содержащихся в уравнениях Максвелла, с учетом того, что система совершает периодическое или почти периодическое движение, имеем

 ,  , (9.4)

где T – характерный период движения;

E и H – характерные средние абсолютные значения напряженностей электромагнитного поля в области пространства, занятой системой зарядов.

Оценку величин и в той же области пространства, можно сделать с учетом того, что поля E и H в реальных системах, совершающих квазистационарное движение, изменяются от точки к точке плавно. Если L – средние размеры системы, то для пространственных производных по порядку величины будем иметь

   . (9.5)

Полученное соотношение (9.5) и является оценочным для пространственных производных уравнений Максвелла для квазистационарных электромагнитных полей.

Так как при условии квазистационарности временные изменения полей происходят достаточно медленно, то в уравнениях Максвелла можно опустить члены, содержащие производные по времени с соответствующим коэффициентом как малые по сравнению с членами, характеризующими пространственное изменение полей. Для этого должны выполняться (по порядку величины) неравенства

; (9.6)

или

, . (9.7)

При этом одновременно должны выполняться приближенные равенства:

, . (9.8)

Разности пространственных производных, входящих в уравнение Максвелла, взаимно компенсируют друг друга, а временные производные (с коэффициентом ) оказываются величинами старшего порядка малости. Из неравенств (9.6) и (9.7) можно получить условие квазистационарности электромагнитного поля

или , (9.9)

где v – характерная скорость движения электрических зарядов.

Из соотношения (9.9) видно, что при квазистационарном движении электрических зарядов их скорости должны быть малы по сравнению со скоростью распространения электромагнитного поля.

С учетом изложенного уравнения Максвелла для квазистационарных электромагнитных полей приобретают следующий вид:

1)

2)

3)

4) (9.10)

Таким образом, в случае квазистационарных электромагнитных полей ток смещения не входит в уравнения Максвелла.

Система уравнений Максвелла оказывается распавшейся на уравнения для независимых полей: магнитного поля токов и электрического поля зарядов.

Объемная плотность электрического заряда в уравнениях (9.10) зависит от времени, как от параметра. В приближении медленно движущихся электрических зарядов решение уравнений для электрического поля приводит к очевидному результату: в каждый момент времени электрическое поле совпадает с электростатическим полем данной системы зарядов.