
- •1. Дифференциальное исчисление
- •1.1. Пределы последовательности и функции
- •1.2. Производные
- •1.3. Исследование функций
- •1.4. Функция двух переменных
- •2. Интегральное исчисление
- •2.1. Неопределенный интеграл
- •2.2. Определенный интеграл
- •2.3. Несобственный интеграл
- •3. Элементы теории множеств и математической логики
- •3.1. Теория множеств
- •3.2. Булева алгебра. Алгебра высказываний
1.4. Функция двух переменных
Основные формулы, определения и теоремы
Определение: Пусть
![]() принадлежит некоторой области
принадлежит некоторой области
![]() на плоскости
на плоскости
![]() .
Если любому
.
Если любому
![]() по правилу
по правилу
![]() ставится в соответствие единственное
значение
ставится в соответствие единственное
значение
![]() ,
то
,
то
![]() называется функцией двух переменных
и
называется функцией двух переменных
и
![]() .
.
Геометрически в
трехмерном пространстве
![]() тройке чисел
тройке чисел
![]() можно сопоставить двумерную поверхность.
можно сопоставить двумерную поверхность.
Определение: Линия уровня
Пусть фиксируется
значение функции
![]() ,
тогда совокупность точек плоскости
,
удовлетворяющих условию
,
тогда совокупность точек плоскости
,
удовлетворяющих условию
![]() называется линией уровня.
называется линией уровня.
Проводя линии уровня с равным известным шагом, можно на плоскости изобразить функцию двух переменных. Например, на географической карте кроме линий уровня для представления высоты точки над уровнем моря используется географическая палитра цветов.
Таким образом, двумерный рельеф местности можно изобразить на плоскости.
Другие примеры линий уровня дают изобарические и изотермические линии.
Функцию двух
переменных можно также представить в
виде плоского черно-белого изображения,
так как в этом случае каждой точке
плоскости
соответствует свое значение
![]() оттенка серого от белого до черного.
оттенка серого от белого до черного.
Определение: Частные производные
Частной производной
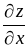 называется производная от
называется производная от
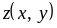 при условии ,что
считается постоянной величиной.
при условии ,что
считается постоянной величиной.Частной производной
 называется производная от
при условии ,что
является постоянной величиной.
называется производная от
при условии ,что
является постоянной величиной.
Определение:
Дифференциалом функции называется
![]()
Определение: Градиент функции
Градиентом функции называется вектор
![]()
Градиент функции указывает направление максимального возрастания функции, т.е. направление максимально крутого подъема в данной точке рельефа. Причем, чем больше модуль градиента
![]()
тем больше скорость возрастания функции, т.е. тем круче подъем.
Определение: Критическая точка
Критической точкой называется точка в которой
![]() .
.
Определение:
Критическая точка называется невырожденной, если определитель
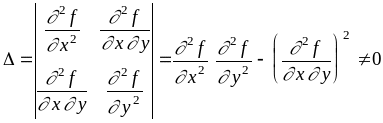
Теорема: Достаточное условие экстремума
Пусть - невырожденная критическая точка функции . Тогда если
 и
и
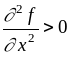 ,
то
- точка минимума;
,
то
- точка минимума;и
 ,
то
- точка максимума;
,
то
- точка максимума;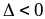 ,
то
- седловая точка.
,
то
- седловая точка.
Примеры решения задач
Пример 1: Найти частные производные и полный дифференциал для функции
![]()
Решение: Считая постоянной, находим
![]()
Считая постоянной, находим
![]()
Полный дифференциал будет равен
![]()
Пример 2: Найти экстремальные точки функции двух переменных
![]()
Решение: Найдем частные производные первого порядка

Приравнивая нулю частные производные, получим систему линейных уравнений для определения критической точки
![]()
отсюда
![]()
Сложив уравнения,
получим
![]() ,
и из второго уравнения получим
,
и из второго уравнения получим
![]() .
Для определения вида критической точки
найдем вторые частные производные
.
Для определения вида критической точки
найдем вторые частные производные
![]()
Отсюда найдем определитель
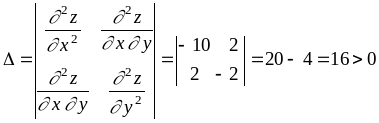
В связи с тем, что
в критической точке
![]() определитель
и
определитель
и
![]() ,
точка
является точкой максимума, а максимальное
значение функции равно
,
точка
является точкой максимума, а максимальное
значение функции равно
![]() .
.
Пример 3: Пусть
задана функция двух переменных
![]() .
.
Тогда частные производные будут равны
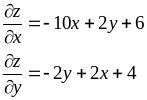
Градиент функции равен
![]() .
.
В точках
![]() и
и
![]() градиент равен соответственно
градиент равен соответственно
![]()
Модули градиентов равны
![]()
Отсюда, в связи с
тем, что
![]() ,
так как
,
так как
![]() ,
функция z
быстрее изменяется в точке
чем в точке
.
,
функция z
быстрее изменяется в точке
чем в точке
.

На рисунке изображены векторы градиента в точках и , указывающие направления максимального возрастания функции.
