2.3. Несобственный интеграл

Основные определения, теоремы и формулы:

Определение: Интеграл от неограниченной функции.

Пусть функция задана на и в точке неограничена. Тогда, несобственным интегралом от неограниченной функции называется предел

.

Определение: Интеграл на бесконечном интервале.

Пусть функция задана на . Тогда несобственным интегралом на бесконечном интервале называется предел

Условие сходимости интеграла от неограниченной функции

Теорема: Пусть функция в окрестности точки эквивалентна . Тогда, интеграл

1. при расходится;

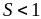2. при сходится.

Условие сходимости интеграла на бесконечном интервале

Теорема: Пусть функция на бесконечности эквивалентна . Тогда, интеграл

1. при сходится;

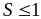2. при расходится.

Примеры решения задач:

Пример 1: Вычислить несобственный интеграл

Решение: Подынтегральная функция обращается в бесконечность в точках 0 и 1. В точке 0 функция эквивалентна , а в точке 1 она эквивалентна . Следовательно, в обоих случаях и интеграл сходится.

Вычислим его

.

Пример 2: Вычислить несобственный интеграл

Решение: Подынтегральная функция при эквивалентна . Следовательно, интеграл - расходится.

3. Элементы теории множеств и математической логики

3.1. Теория множеств

Основные определения, теоремы и формулы:

Элементы теории множеств

Множество  самое абстрактное понятие математики.

Это понятие настолько общее, что трудно дать ему какое-либо определение, которое не сводилось бы к замене слова «множество» равнозначными выражениями «совокупность», «собрание элементов» и т.д.

Все же дадим определение.

Определение. Множество  это совокупность элементов.

Множества будем обозначать прописными буквами А, В, С , а их элементы  малыми a, b, c 

Утверждение «элемент а принадлежит множеству А» символически записывается означает «элемент а не принадлежит множеству А».

Определение. А является подмножеством В, если из вытекает, что . Обозначается .

Операции над множествами

Определение. Пусть А и В  произвольные множества. Суммой или объединением двух множеств называется множество, состоящее из элементов множества А или В, или обоих множеств одновременно.

Определение. Произведением или пересечением множеств называется множество, принадлежащих множеству А и В одновременно.

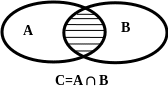
Свойства объединения и пересечения множеств

1. 1. 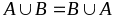, коммутативность .

2. .

2. 1. , ассоциативность.

2. .

3. , дистрибутивность

4. .

Определение. Дополнение к множеству А.

Пусть   некоторое множество и пусть А является подмножеством . Тогда дополнением к А называется множество , состоящее из элементов, не принадлежащих к А, но принадлежащих .

Свойство. .

Теорема двойственности.

Примеры решения задач:

Пример1. Для заданных множеств на плоскости А и В убедится в справедливости теоремы двойственности (теоремы о дополнении к объединению множеств) .

Пусть . Нарисуем множества А и .

Затем построим множества и множества .

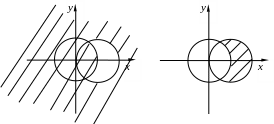
Таким образом, будет построена левая часть теоремы двойственности.

П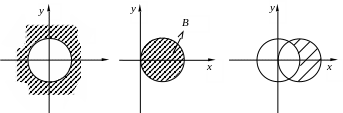 остроим теперь правую часть .

Из рисунков видно, что множества и совпадают, то есть = .

Задача 1: Для заданных на плоскости (x, y) множеств А и В найти А  В, На данном примере убедится в справедливости теорем о дополнении к объединению или пересечению множеств то есть в справедливости тождеств .

1. A =  x ² + y ² 1, B =  (x - 1) ² + y ² 1

2. A =  x ² + y ² 1, B =  (x - 1) ² + (y - 1) ² 1

3. A =  x ² + y ² 1, B =  x ² + (y - 1)² 1

4. A =  x ² + y ² 1, B = 0 x 1; 0 y 1 

5. A =  x ² + y ² 1, B =  (x - 1) ² + y ² 2

6. A = 0 x 2; 0 y 2 , B = -1 x 1; -1 y 1 

7. A = 0 x 1; 0 y 1 , B =  (x - 1) ² + (y - 1) ² 1

8. A =  x ² + y ² 1, B = 0 x 3; 0 y 1 

9. A = -3 x 3; -1 y 1 , B = -1 x 1; -3 y 3 

10. A = -4 x 4; 0 y 2 , B = 0 x 2; -4 y 4 