Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
Основные свойства определенного интеграла.
1. =0
Если а>b, то по определению = - (4), т.е. когда отрезок [a,b] при a<b пробегает в направлении от b к а, имеем b=X0, а=Xn, Xi=Xi-Xi-1<0
2. =
+
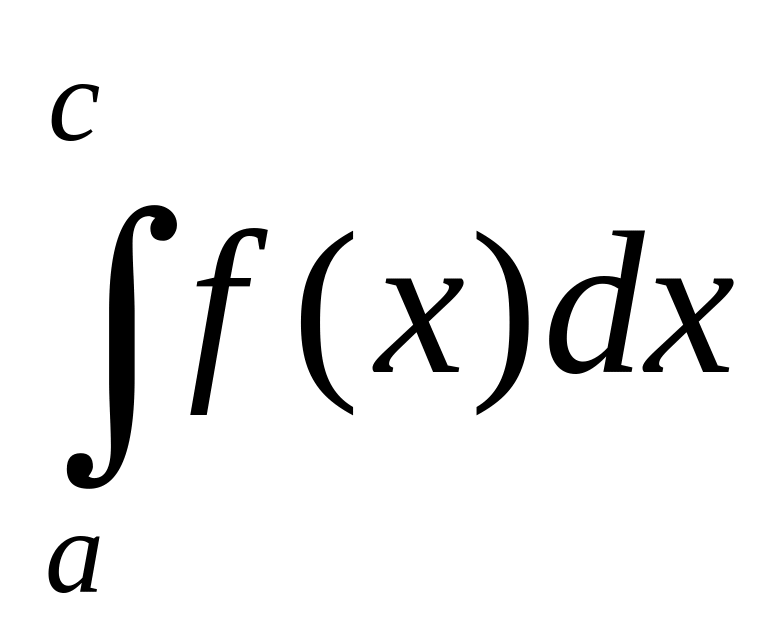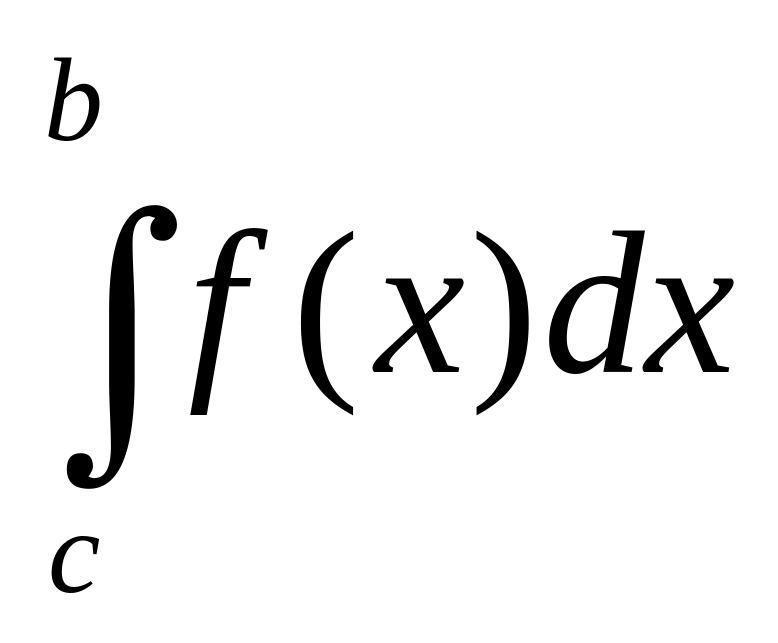(здесь и в дальнейшем предполагается,
что интегралы, входящие в доказываемые
формулы существуют)
Доказательство:
Допустим сначала, что а<c<b,
т.к. предел интегральной суммы
не зависит от способа разбиения отрезка
[a,b],
то будем проводить разбиение так, чтобы
точка с всегда была бы точкой разбиения
[a,b].
Если например с=хm,
то
можно разбить на две суммы: =
=
+
.
Переходя в последнем равенстве к пределу
при
мы и получим искомое равенство.
Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство
для другого расположения точек a,
b, c легко сводится к рассмотренному
случаю. Пусть, например, а<b<c,
тогда по доказанному, имеем:
=
+
,
откуда учитывая (4) получаем
=
-
=
+
,
ч.т.д.
Постоянный множитель можно выносить за знак определенного интеграла, т.е.
=к
.
Доказательство: действительно, для
любого разбиения отрезка [a,b]
и любого выбора точек I
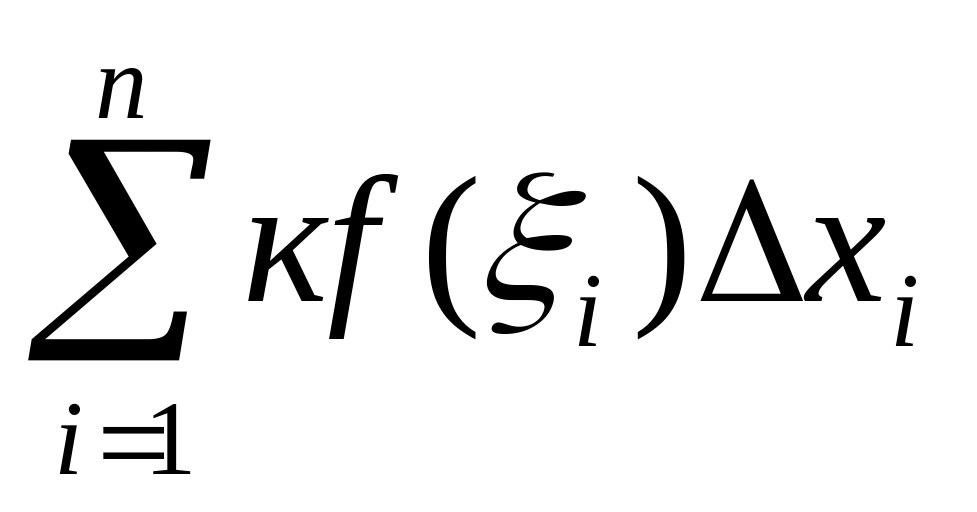=k
Переходя
к пределу при 0
имеем
=
=
=к
=
к
.,
ч.т.д.
Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
.
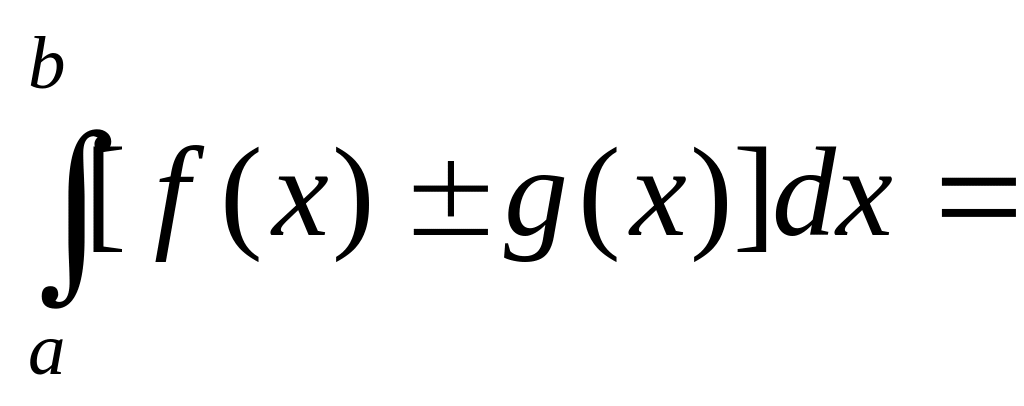
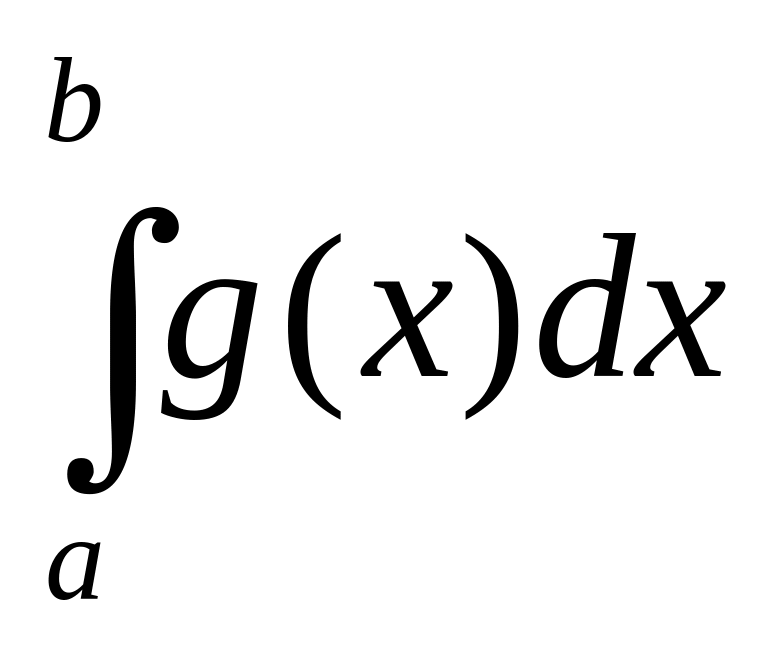Доказательство: действительно, для
любого разбиения отрезка [a.b]
и любого выбора точек I
=
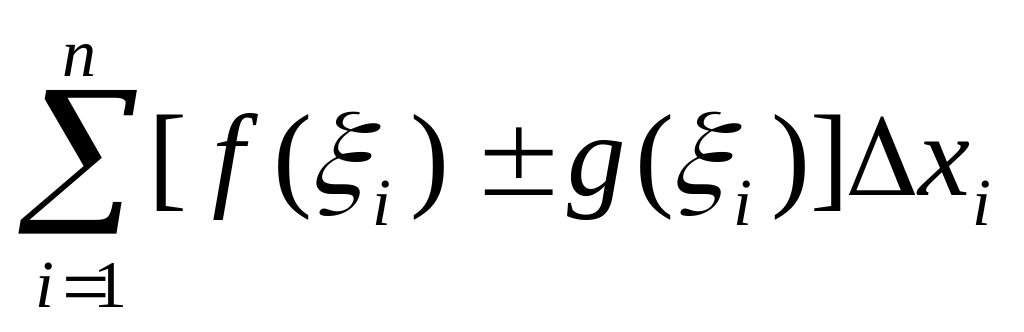Так
как
=
и
=
,
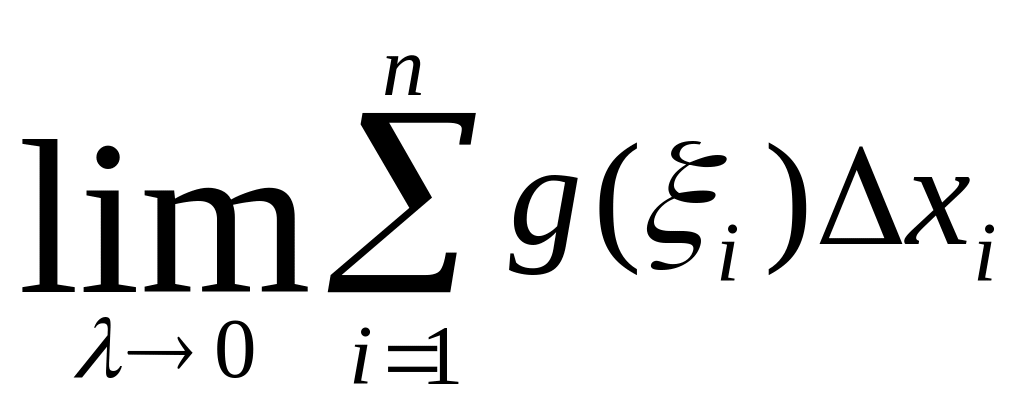то получаем что
=
=
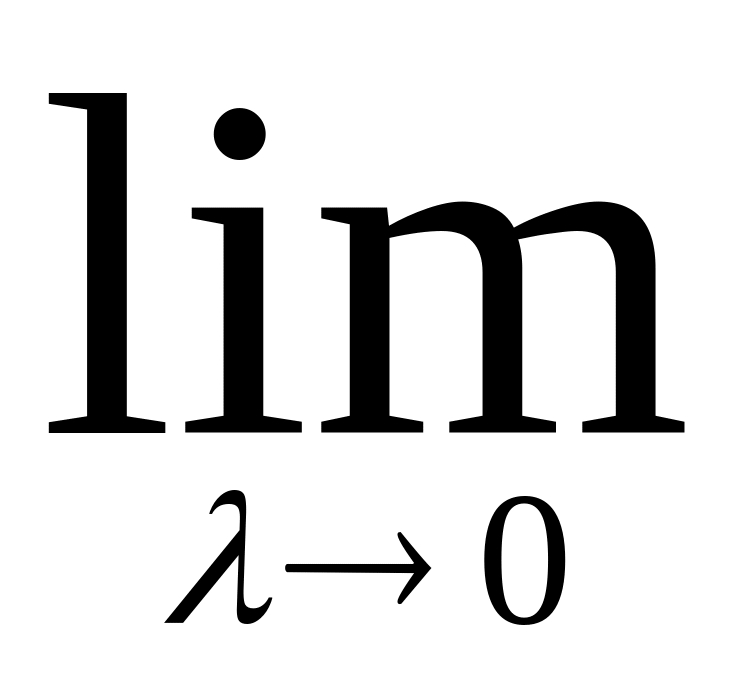Оценки интегралов. Формула среднего значения.
[Т] Если функция f(x) непрерывна на сегменте [a,b] то существует т С, принадлежащая этому сегменту, такая что =f(c)(b-a). Эта формула называется формулой среднего значения.
Замечание: теорема о среднем имеет четкий геометрический смысл: величина определенного интеграла при f(x)>=0 равна площади прямоугольника имеющего высоту f(c) и основание b-a.
[Т] Пусть а<в.
Если f(x)≥0 для любого х€[a,b]→∫от а до в f(x)≥0
Если f(x) ≥g(x) для любого х€[a,b]→∫f(x)dx≥∫g(x)dx
Если f(x) опред на [a,b]→|∫f(x)dx|≤∫f(x)dx
Если |f(x)|≤k для любого х€[a,b]→|∫f(x)dx|≤k*(b-a)
Пусть m,M соответств наим и наиб значения ф-ии f(x) на [a,b],тогда справедлива ф-ла m(b-a)=∫f(x)dx≤M(b-a)
Интеграл с переменным верхним пределом.
Интеграл с переменным верхним пределом.
x
[a,b]
Это интеграл у которого нижний предел а=const а верхний предел х переменный. Величина этого интеграла представляет собой функцию верхнего предела х
(х)= , где х принадлежит сегменту [a,b] и ф(х)= интеграл с переменным верхним пределом. Геометрически интеграл с переменным верхним пределом представляет собой S криволинейной трапеции.
[Т] Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т.е. Ф’(x)=( )’x=f(x)
Ф’(x)=( )’=f(x)
Ф’(x)=
Замечание. Т.о., любая непрер на отрезке функция f(х) имеет на этом отрезке первообр, которой явл интергал с перемен верхним пределом Ф(х),т.к. любая др первообр может отлич на константу,то сущ связь между опр и неопр интегралом.