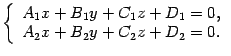Вопрос 9.

Угол между плоскостями

Пусть плоскости   и   заданы соответственно уравнениями   и   . Требуется найти угол   между этими плоскостями.

Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку   на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры   и   к линии пересечения. Нарисуем также нормальные векторы   и   плоскостей   и   с началами в точке   (рис. 11.6).

Рис.11.6.Угол между плоскостями

, где

(A₁, B₁, C₁), (A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения:

.

  Таким образом, угол между плоскостями находится по формуле:

 

 

 Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

  На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

 Плоскости параллельны, векторы нормалей коллинеарны:  .Это условие выполняется, если: .

 

Угол между прямыми в пространстве.  Пусть в пространстве заданы две прямые. Их параметрические уравнения:

l₁: 

l₂: 

 

 Угол между прямыми  и угол между направляющими векторами  этих прямых связаны соотношением:  = ₁ или  = 180⁰ - ₁. Угол между направляющими векторами находится из скалярного произведения. Таким образом: .

Вопрос 10

Каноническое уравнение прямой в пространстве. Пример.

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой принадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

Итак, если уравнения двух непараллельных плоскостей -- и , то прямая, являющаяся их линией пересечения, задается системой уравнений

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Уравнения (11.11) называют общими уравнениями прямой в пространстве.

Каноническое уравнение прямой в пространстве

Уравнения прямой, проходящей через точку параллельно вектору (канонические уравнения прямой)

Пусть прямая проходит через точку  параллельно вектору . Так как любой ненулевой вектор, параллельный данной прямой, является ее направляющим вектором, то для любой точки , лежащей на данной прямой, вектор  коллинеарен направляющему вектору . Поэтому их соответствующие координаты должны быть пропорциональны, следовательно, имеют место равенства: ,

называемые каноническими уравнениями  прямой в пространстве.