Вопрос 5. Обратная матрица: определение, теорема о существовании.

Если А – квадратная матрица, то обратной по отношению к ней называется матрица, которая будучи умноженной на А как справа, так и слева дает единичную матрицу. А^-1 *А=А* А^-1 =Е

Только квадратная матрица имеет обратную матрицу. Если обратная матрица А^-1 существует, то матрица А называется обратимой.

Операция вычисления обратной матрицы называется обращением матрицы.

Теорема: Для того, чтобы квадратная матрица А имела обратную матрицу необходимо и достаточно, чтобы матрица была вырожденной, т.е модуль А не равен нулю. Алгоритм вычисления обратной матрицы:

1)Находят определитель матрицы А

2)Находят алгебраические дополнения всех элементов матрицы А и записывают новую матрицу.

3)Транспонируют полученную матрицу.

4)Умножают полученную матрицу на 1/модуль А

Пример: Дана матрица 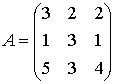 . Найти обратную матрицу.    Р е ш е н и е: Вычисляем определитель матрицы A:

   Находим алгебраические дополнения элементов этого определителя:

,    ,    ,    ,   

,    ,   

   Следовательно,

Вопрос 6.

Нахождение обратной матрицы методом Жордана-Гаусса.

Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы.

Алгоритм:

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры   раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

Пример:

Для решения следующей системы уравнений:

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

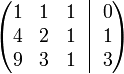
Проведём следующие действия:

• К строке 2 добавим: −4 × Строку 1.

• К строке 3 добавим: −9 × Строку 1.

Получим:

• К строке 3 добавим: −3 × Строку 2.

• Строку 2 делим на −2

• К строке 1 добавим: −1 × Строку 3.

• К строке 2 добавим: −3/2 × Строку 3.

• К строке 1 добавим: −1 × Строку 2.

В правом столбце получаем решение:

 .