7. Проверка гипотез как задача теории статистических решений. Пример совпадения байесовского решающего правила и классического подхода к проверке гипотез.

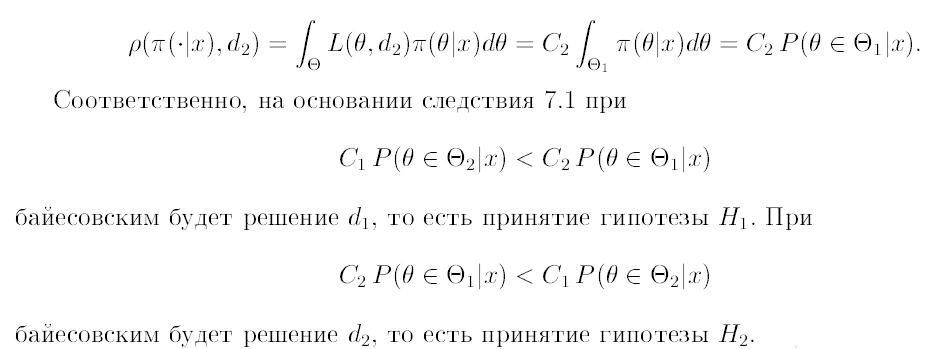
8. Доверительные интервалы. Множества наивысшей апостериорной плотности. Доверительные множества наивысшей апостериорной плотности.

Пусть имеется выборка X₁...X_n из некоторого закона распределения, и мы хотим оценить параметр этого закона θ – это может быть, например, математическое ожидание или дисперсия. Доверительным интервалом для параметра θ с уровнем доверия β мы будем считать такой интервал (A; B), что P(A<θ<B) = β. Задача интервального оценивания – найти такие границы A и B.

То, что следует запомнить: доверительный интервал тем шире, чем выше уровень доверия.

Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и известной дисперсии.

Выражение для 100(1-α)% доверительного интервала для μ, рассчитываемое по набору наблюдений x₁...x_n при знании дисперсии σ²:

(1)

,где - это среднее, рассчитанное по имеющемуся набору наблюдений.

Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и неизвестной дисперсии. В случае неизвестной дисперсии 100(1-α)% доверительный интервал для математического ожидания имеет следующее выражение:

(2)

Доверительный интервал для математического ожидания (μ) в случае большого объёма выборки. Доверительный интервал для математического ожидания свободно распределённого признака (случайной величины) при неизвестной дисперсии и большом объёме выборки может быть записан так:

(3)

Здесь z, такое число, что , .

Доверительный интервал для доли объектов с заданным свойством в генеральной совокупности (p) в случае большой выборки. Выборочное среднее в этом случае есть выборочное отношение .

По таблицам стандартного нормального распределения найдём число z, такое что . Таким оборазом, выражение для 100(1-α)% доверительного интервала для p:

(4)

Доверительный интервал для дисперсии (σ²) в случае нормальной генеральной совокупности. Нам понадобятся числа и , такие что и .

.

100(1- α)% доверительный интервал для дисперсии выглядит так:

. (5)

Доверительный интервал для разности математических ожиданий в случае нормальной генеральной совокупности: парные наблюдения

, (6)

где - как и раньше, такое число, что (т.е. U имеет t-распределение Стьюдента с n-1 степенью свободы) или, иначе, .

Выражение (6) – это и есть выражение для доверительного интервала для разности математических ожиданий.

Доверительный интервал для разности математических ожиданий в случае нормальной генеральной совокупности и известных дисперсий: независимые выборки.

Рассмотрим случайную величину – разность выборочных средних: . Её математическое ожидание равно оцениваемому параметру:

.

Её дисперсия выражается следующим образом:

.

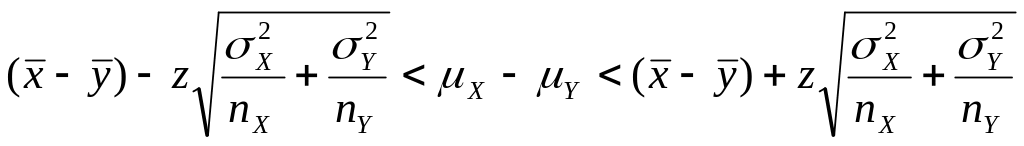(7)

Доверительный интервал для разности математических ожиданий в случае нормальной генеральной совокупности, неизвестных дисперсий и большого объёма выборки: независимые выборки. В данном случае мы можем пользоваться выражением (7), подставляя туда выборочные дисперсии на место истинных:

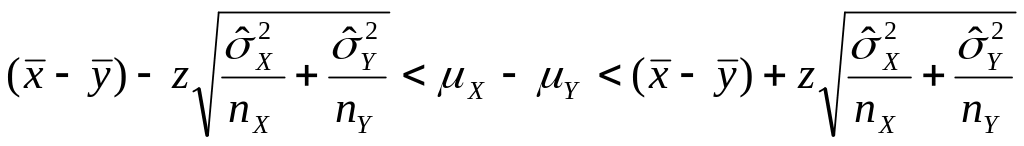(8)

Доверительный интервал для разности математических ожиданий в случае нормальной генеральной совокупности и неизвестных (но равных между собой) дисперсий: независимые выборки.

(9)

Здесь , а - такое число, что , где - случайная величина, имеющая t-распределение со степенями свободы (n_X+n_Y-2). Соответственно, .

Множества наивысшей апостериорной плотности. Доверительные множества наивысшей апостериорной плотности.

Пусть условная функция плотности f(x|θ) – это функция плотности нормального распределения с известным ожиданием и с точностью θ,

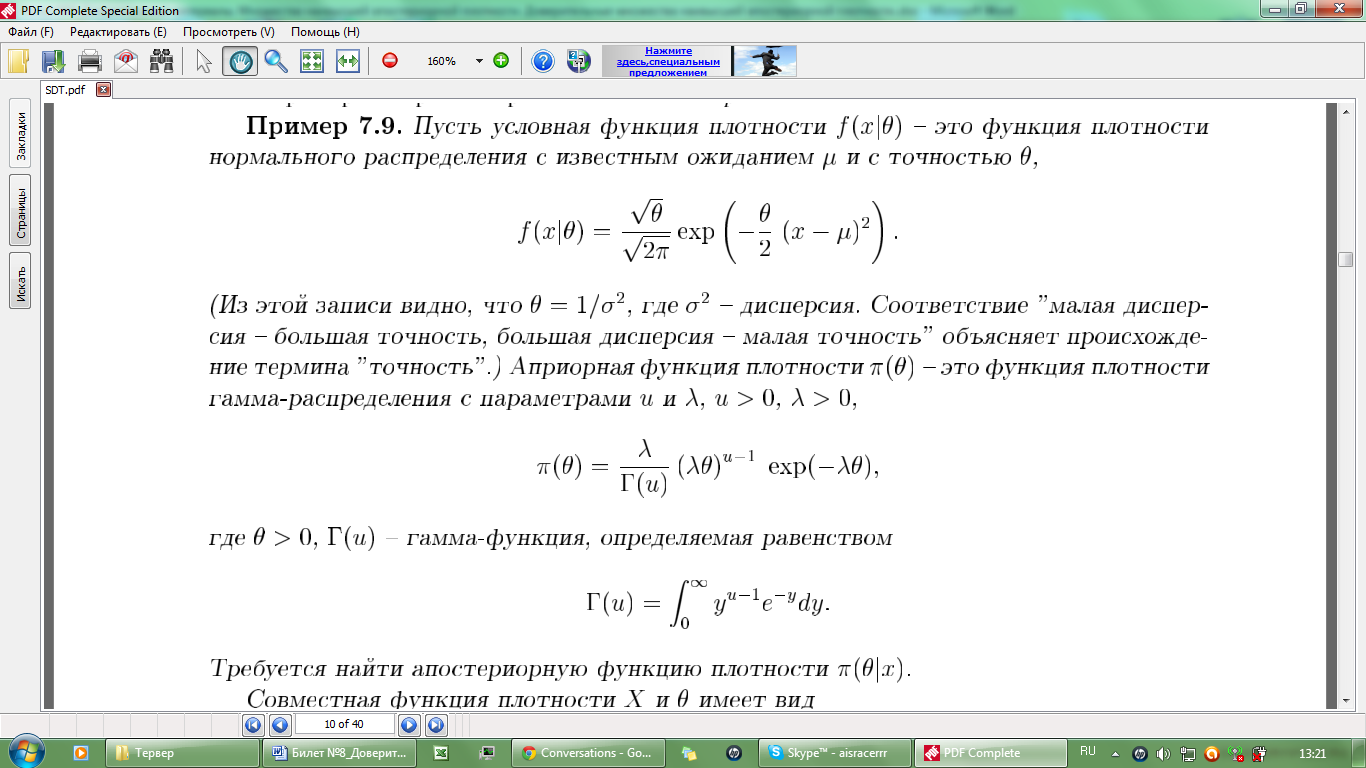
Найдем апостериорную функцию плотности :