Элементарными являются следующие булевские функции. Функции одной переменной:

1. Тождественный ноль (эта функция обозначается как O(x) или 0).

2. Тождественная единица (обозначается как 1(x) или 1).

3. Отрицание, записываемое как .

4. Тождественная функция (обозначается как I(x) или x).

Табличные задания данных функций имеют следующий вид:

x	0(x)	1(x)		I(x)
0	0	1	1	0
1	0	1	0	1

Функции двух переменных:

1.  (x₁, x₂) - дизъюнкция;

2. & ( x₁, x₂) - конъюнкция;

3.  (x₁, x₂) - импликация;

4. + (x₁, x₂) - сумма по модулю два;

5. ~ (x₁, x₂) - эквивалентность;

6.  (x₁, x₂) - функция Шеффера.

На практике для представления этих функций используется инфиксная запись, в которой символическое имя функции записывается между левой и правой компонентой аргумента, т.е. например, вместо & (x₁, x₂) используется запись: (x₁ & x₂).

Табличные задания этих функций приведены в следующей таблице:

x1 x2	x1 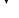x2	x1& x2	x1 x2	x1+x2	x1~x2	x1 | x2
0 0	0	0	1	0	1	1
0 1	1	0	1	1	0	1
1 0	1	0	0	1	0	1
1 1	1	1	1	0	1	0

Заметим, что отнесение приведенных функций к элементарным достаточно условно. Например, нетрудно проверить, что совпадает с отрицанием конъюнкции, т.е. одни элементарные функции могут быть выражены через другие такие функции.

4.5. Формулы

С помощью символических обозначений переменных и функций можно строить записи, представляющие другие булевские функции. Такие записи называются формулами.

Пусть B  произвольное множество булевских функций. Определим понятие формулы над B.

Определение

1. Если f(x₁, . . . , x_n) B, то запись f(x₁, . . . ,x_n) является формулой над B.

2. Пусть f ( x₁ , . . . , x_n ) B и A ₁ , . . . , A _n  это либо формулы над B, либо обозначения переменных. Тогда запись f(A₁, . . . , A_n)  формула над B.

3. Никакие другие записи не являются формулами над B.

Примером формулы над множеством элементарных функций является следующая запись:

.

Пары ограничивающих скобок в формулах необходимы для определения порядка вложенности одних формул в другие. При этом всякая формула, вложенная или содержащаяся в другой формуле, называется подформулой такой формулы.

Важной характеристикой подформул является глубина их вхождения в формулы:

1. Вхождения переменных во всякую формулу имеют глубину 0.

2. Если f (x₁, . . . , x_n) B, то формула U = f (x₁, . . . , x_n) имеет глубину d(U)=1

2. Если U = f (U ₁, . . . , U_n), то глубина U определяется соотношением: d(U)= 1 + max(d(U₁), . . . , d(U_n)).

Для обозначения формул используются прописные символы латинского алфавита (возможно с индексами). Если в записи формулы U содержатся символы переменных x₁, . . . , x_n, то допускается запись этой формулы в виде U(x₁, . . . , x_n). Если U содержит подформулы U₁, . . . , U_k, то для указания на это свойство формулы U используется запись U(U₁, . . . , U_k).

Записи формул над множеством элементарных функций можно упростить за счет опускания части скобок. Для этого достаточно ввести понятие приоритета или старшинства функций из этого множества.

Приоритеты или старшинство элементарных функций устанавливаются следующей схемой убывания приоритетов:

1) 0, 1, I;

2) ;

3) &, ;

4) +, ~, ,.

Приоритеты означают, что при отсутствии скобок более сильная операция соответствует подформуле большей вложенности, или применяется раньше. Тогда с учетом приоритетов приведенный ранее пример формулы можно переписать в виде: .

Всякая формула U (х₁, . . . , х_n) представляет однозначно определяемую булевскую функцию f _U (x₁ , . . . , x_n). Напомним, что x₁, . . . , x_n  это все переменные, входящие в U.

Для определения значения f _U на конкретном наборе значений переменных x₁ , . . . , x_n можно воспользоваться следующими правилами:

1. подставим в U вместо переменных x₁, . . . , x_n принимаемые ими значения;

2. вычислим значение произвольной наиболее вложенной функции, все переменные которой принимают конкретные значения, и заменим вхождение этой функции в формулу на полученное значение;

3. если полученная в результате запись не является двоичным значением, то повторим действие 2.

Понятие формулы над множеством функций B и понятие функции, представляемой формулой, не являются эквивалентными и не равносильны поскольку всякая формула  это запись, представляющая некоторую булевскую функцию f, но сама такая функция может представляться различными формулами.

Например, нетрудно убедиться, что следующие две формулы над множеством элементарных функций представляют одну и ту же функцию: U₁ = и .