4. Оператор энергии

У нас был один из постулатов, что существует оператор , который называется гамильтонианом и который определяет динамику системы, то есть изменение вектора состоянияза единицу времени получается как результат действия операторана вектор состояния в данный момент времени:

Это аналог Второго закона Ньютона. Этот оператор что такое?

Для частицы в потенциальном поле силгамильтонианH– это полная энергия частицы, выраженная через координаты и импульс:. Тогда операторпо нашему рецепту будет:

Задача на собственные векторы оператора энергии ставится так: оператор действует на вектор, даёт число,:. В координатном представлении векторызадаются функциями:. Для частицы в связанном состоянии спектр собственных значений оператора энергии дискретен (энергия в этом случае квантуется), в несвязанном состоянии спектр собственных значений непрерывен (энергия не квантуется). То есть, если частица может уйти на бесконечность, то любое действительное число может представлять её энергию, а если не может уйти на бесконечность, то тогда энергия может принимать определённые значения. Как найти эти собственные значения и собственные векторы?

В координатном представлении оператор изобразится так:

Тогда уравнение на собственные значения перепишется в координатном представлениитаким образом:. Сейчас мы его перепишем так:. Это уже знакомое уравнение, это уравнение Шредингера для стационарных состояний. Это означает то, что мы с вами делали, мы решали задачу на собственные значения оператора энергии.

Для свободной частицыдолжно оказаться, что спектр собственных значений непрерывен, проверим. Для свободной частицы никакой потенциальной энергии нет:. Тогда задача на собственные векторы приводит к такому уравнению:(я не пишу индексы, потому что на самом деле они и не появятся) или, обозначим, тогда легко убедиться, что функцияявляется решением этого уравнения.¹)

Собственные значения нумеруются вектором , мы можем написать так:,или в координатном представлении. Мораль такая: задайте любой вектор, этому вектору будет отвечать функцияс таким собственным значением:. И, действительно, мы видим, что спектр собственных значений непрерывен, потому что векторлюбой.

5. Оператор импульса

Физическая проблема такая: энергия квантуется, координата, как мы видели, не квантуется, спрашивается, квантуется ли импульс (то есть в результате измерений может получаться любое число или какие-то дискретные величины)?¹)

В координатном представлении оператор импульса есть: . Уравнение на собственные векторы выглядит так:, в координатном представлении векторзадаётся некоторой функциейи должен изобразиться так:, а уравнение на собственные векторы в координатном представлении сводится к такому, и в компонентах:или. Посколькуэто функция отxтолько, то можно писать прямую производную:

Решение находится сразу: . Общий результат такой:

Это собственная функция оператора импульса, отвечающая собственному значению . Можно рассматривать это как наводящие соображения. Вернёмся к уравнению.

Утверждение.Функцияявляется решением этого уравнения.

Доказательство.Подставляя эту функцию в уравнение, мы получаем:

Функция является собственной функцией оператора импульса, соответствующей собственному значению.

Отсюда видно, что собственным значением оператора импульса может быть любой вектор.

Если операторы двух переменных коммутируют, то эти переменные могут быть заданы и измерены одновременно, а операторы имеют одинаковые собственные векторы, ну и поэтому собственные значения могут быть заданы одновременно. То, что нельзя одновременно задавать координату и импульс, мы обсуждали, можно ли одновременно задать координату и энергию? Ответ зависит от того, коммутируют или нет операторы координаты и энергии. Ответ такой: оператор энергии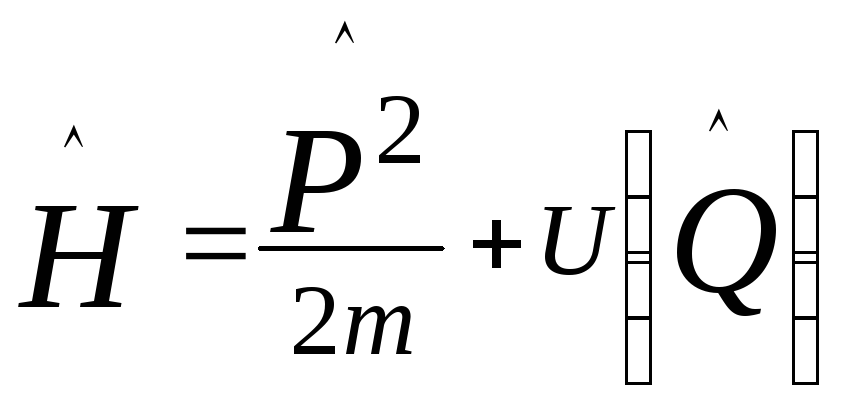, очевидно, что операторы и не коммутируют, потому что операторсо вторым слагаемым прокоммутирует, а с первым нет (это следует из коммутационного соотношения). Это означает, что координату и энергию задать вместе нельзя никогда, то есть не может быть утверждений, что частица находится в некоторой точке пространства и имеет такую-то полную энергию (они не коммутируют). Другой вопрос: импульс и энергию задать можно или нет? Вроде бы ответ напрашивается, что в коммутационное соотношение координата и импульс входят симметрично, нооператор энергии координата и импульс входят несимметрично,. Например, для свободной частицы, когда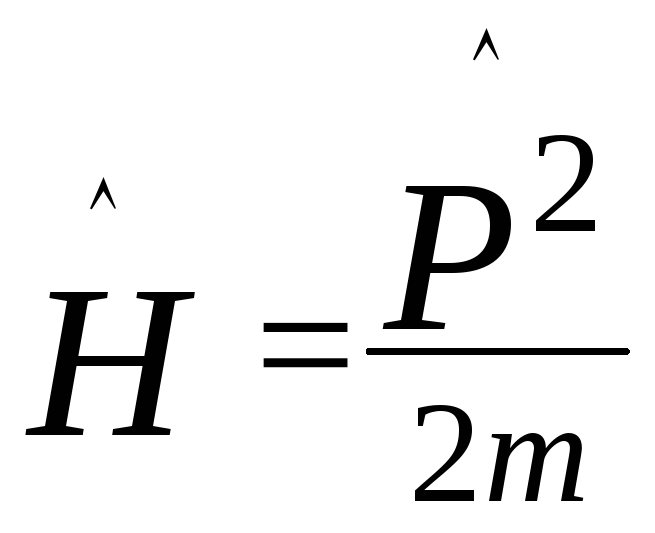, оператор импульса с оператором энергии прокоммутирует. И, стало быть, импульс и энергия свободной частицы могут быть измерены одновременно. И действительно, это мы уже видели, а функцияявляется одновременно собственной функцией оператора импульса и энергии, собственные значения связаны так:,. Но если частица не свободна, то оператор импульса не коммутирует с оператором энергии.

11

Мы нашли, что , и мы нашли вид этого вектора в координатном представлении:.¹) Векторымогут быть выбраны сами в качестве базиса, в котором можно выражать все другие векторы, это называетсяимпульсное представление.

Чтобы покончить совсем с оператором импульса и собственными значениями оператора импульса, окончательно оформим это так: оператор действуя на вектордаст:, при этомсобственныезначения оператора будут равняться, а векторизобразится так:.