Глава IV нормальный закон распределения

§ 1. Понятие о нормальном законе распределения

4.1Л. Зкачевие норйально1ю закона распределения. В первой главе было освещено фундаментальное значение нормального закона распределения в теоретическом и практическом отношениях. Теперь мы подробно рассмотрим свойства этого распределения и его про­стейшие приложения.

4.1.2. Нормальная плот- ность вероятности и ее параметры. Нормальной плотностью вероятности называется плотность, опре­ деляемая равенством ^:

/2яс

п (х; а; а) =

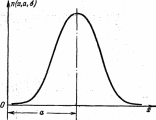
для любого значения — оо-< <лг<Соо, где а и а—произ­ вольные числа (параметры ^!р_ис. 29. График нормальной плотности распределения), причем а вероятности.

положительно. Соответст­вующая -этой плотности дифференциальная кривая распределения показана на рис. 29.

Интегральная функция нормального распределения по соотноше­нию (3.2.10) определяется > из, (4,4.1») в виде

М(х; а; а) = п (х; а; а) их.

(4.1.2)

Легко видеть» что при любом х, каковы бы ни были параметры а и а> 0, всегда п (х; а;,а);> 0_ С другой стороны, полная площадь

134 Нормальный закон распределения

под всей кривой выразится интегралом

= 1 г

^2яо ]

/=

[ГЛ. IV

(4.1.3)

который путем замены переменного х на « = - (откуда х=а-}- аи

и (х =

,^ 1 Г /2^ ]

так как ввиду того, что а>0, верхнему пределу х= + °° ^в (4.1.3) соответствует такой же верхний предел в (4.1.4) и аналогичное соответствие имеется между нижними пределами этих интегралов.

преобразуется в интеграл / =

(4.1.4)

0,75

0,5

а-зи

а-в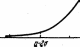

а+б

а+Зб

Рис. 30. График нормальной интегральной функции распре­деления.

Мы видим, что площадь под «любой» нормальной кривой (при любых а и а) такова же, как под нормальной кривой с параметрами а = 0 и а=1. Другими словами, эта площадь не зависит от пара­метров; значение интеграла / равно единице¹). Таким образом, выполнены условия (3.2.5) и (3.2.6) для плотности распределения вероятности и функция п (х; а; а) при всех возможных значениях

') См., например, упомянутую в предисловии «Общую часть», стр. 119—120.

§ 1] Понятие о нормальном законе распределения 135

параметров — оо«<а<Соо и а>0 является плотностью распреде­ления.

График интегральной функции распределения показан на рис. 30.

Из (4.1.1) и рис. 29 видно, что нормальное распределение сим­метрично относительно ординаты, отвечающей значению а;, равному а. Это значение является поэтому центром группирования (матема­тическим ожиданием) распределения. Если изменять а, то кривая у — п (х; а; а) будет перемещаться вдоль оси х, сохраняя свою форму. С возрастанием абсолютной величины уклонения (х — а), т. е. по мере удаления точки х от точки а, ордината кривой п (х-, а; о) быстро убывает; наибольшая ордината, отвечающая значению х=а,

имеет величину . — — = я(а; а; а). Эта ордината и является осью У 2л о

симметрии кривой. При а = 0 имеем семейство центрированных (т. е. с центром в начале координат) нормальных кривых

-—

*°' = п(хг, 0; а), (4.1.5)

зависящих от одного параметра а.

Когда параметр а уменьшается, начальная ордината кривой растет. Подъем кривой в центральной части компенсируется более резким спадом ее к оси х, так что общая величина площади, как мы видели, остается неизменной и равной единице. При очень малых значениях а кривая становится похожей на тонкую иглу, направленную вдоль оси у. Почти вся площадь под кривой сконцентрирована на неболь­шом интервале с центром в нуле. При возрастании а, наоборот, происходит «сплющивание» кривой, принимающей все более плоско-вершинную форму (рис. 31).

Чаще всего, однако, рассматривая величину, подчиненную нор­мальному закону N(x•, а; а), переходят к нормированному распре­делению. Нормирование распределения, вообще говоря, заключается в переходе от величины X к вспомогательной линейной функции

для которой

(4.1.6)

При нормальном распределении из (4.1.6) и (4.1.2) будем иметь:

« + » (ц-а)'

Р (Л < а + га) = N (а + га; а; а) = • -_ е~ *°° аи,

2яа

|А2яа .

. —во

136

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

[ГЛ. IV

откуда ( заменяя переменное интеграции и на новое v, пользуясь

подстановкой

г>==— — - ""и й?г> = — ) о ;-.... 0 }

получим:

(4.1.7)

Дифференцируя (4.1.7) по верхнему пределу, получим:

1

; 0;

__

(4.1.8)

Таким образом, если произвести нормирование распределения п(х; а; а), .т* е. осуществить переход от величины X;,«..величине 2,

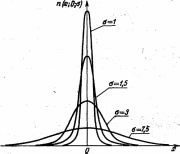
Рис. 31. Семейство «центрированных» нормальных кривых распределения 0=1; 1,5; 3; 7,5.

то плотность вероятности 2 выразится равенством (4.1.8), в котором уже отсутствуют параметры а и а. Все вопросы; связанные с нор­мальным распределением величины X, решают, переходя к вспомо­гательной величине 2., т. е. нормируя это распределение.

Нормирование распределения, как нетрудно понять, ведет-проста, к перенесению начала координат в центр группирования, т. «.-к «центрированию» и к выражению абсциссы в долях а, которое, как мы дальше увидим, представляет среднее квадратическое откло­нение величины X, т. е. а = а_х.

§ 11

ПОНЯТИЕ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

137

Ординаты кривой (4.1.8) табулированы. В таблице I приложений приведены значения этих ординат для значений г от 0 до 4,99. Эта таблица используется, в частности, для построения теоретической кривой распределения, когда эмпирическое распределение непрерыв­ной величины хотят глазомерно сравнить с нормальным распреде­лением.

Пусть, например, мы хотим провести такое сравнение распре­деления, приведенного в таблице 3.2.6. Мы приближенно определяем неизвестные нам параметры а и 0 нормального распределения по опытным данным: параметр а мы приравниваем средней арифмети­ческой отклонений размеров

а а?х ==4-4,3 мк :

и параметр |р?-нри$шш1иваем среднему квадратическому отклонению эмпирического распределения

0?*** I/ с —— 07 */*/• /**^ У О — С7 | I и/ТУП?

{эмпирические характеристики нами были подсчитаны в п. 3.2.4). Законность подобного приближенного определения параметров нами будет оправдана далее. Таким образом, мы получили нормаль­ную плотность в виде

п(х; 4,3; 9,7) =

/2я9,7 * ЛИГ"

Пронормируем это распределение. Для этого ширину интервалов выразим в долях о* и получим, что при Ах = 5 мк и 0=9,7 мк ширина &г в долях а равна

•:• ^; ' • ' ' '•••••' ^: " а ' &Х 5

Перенеся начало координате точку х= -\-4,3 мк, получим абсциссу середины первого интервала в долях 0 в виде

г — **—^й_ —17,5—4,3_ ₉ „ ^г1—5-~ д^—~"^*,ш.

Учитывая, что Аг;==0,515, далее получим:

г_ъ = — 2,247 + 0,515 = -^ 1,732, ^ = —1,7324:0,515 = —1,517, ;

,и т. д. (см. строку 2 таблицы 4.1.1).

Для этих точек мы находим по таблице I приложенийI значения йлоуйости (4.1.8) для величины 2, проставленные в строке 3 таблицы 4.1.1.

Помножая эти величины на ширину интервала Аг, найдем при­ближенную величину площади под кривой в каждом интервале,

§ И

ПОНЯТИЕ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

139

характеризующей вероятность попадания в него. Ее естественно сопоставить с наблюденными в выборке частостями чи(^/приведен­ными в строке 5 таблицы 4.1.1, для чего последние можно пред­ставить в виде площадей прямоугольников, построенных на интер­валах. Тогда, очевидно, ординаты этих прямоугольников будут равны

-г-^ (см. строку 6 таблицы 4.1.1). Пользуясь последними, мы строим

гистограмму распределения, а через точки, отвечающие плотностям р(г), проводим соответствующую нашей гистограмме нормальную кривую распределения (рис. 32).

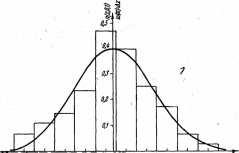
-1&7 -0,702 -Ц1870 +Ш +0.8Я +1,358 +1,873 +2,388 г

Рис. 32. Гистограмма распределения 200 валиков по диаметрам,

совмещенная с графиком нормальной плотности вероятности

п (г; 0; 1) при «=^# = 4,3 мк и а = 5 = 9,7 мк.

Мы видим, что гистограмма нормированного распределения, естественно, имеет такой же вид, как и гистограмма, показанная на рис. 27, только здесь по оси абсцисс отложены не микроны,

вместо отношений

а доли а и по оси ординат — отношения

• -< - , использованных при построении рис. 27.

1\л

Из рис. 32 видно, что полученное из наблюдений эмпирическое распределение валиков по диаметрам довольно хорошо согласуется с нормальным распределением, так как лишь сравнительно неболь­шие участки гистограммы выходят за пределы кривой нормальной плотности. Однако такое глазомерное сравнение распределений является весьма приближенным; более точное сравнение выполняется с помощью специальных критериев, рассматриваемых в дальнейшем.

54

Анализ распределения

[гл

коэффициента формы лапландской сооны (Ршиз 1аррошса) V

в возрасте 120—160 лет (по данным Кольской экспедиции 1929 г.):

Коэффициент формы, % ... 53 57 61 65 69 73 77 81 85 89 Сумма Число деревьев 1 — 6 20 42 65 47 23 11 1 216

мера изменчивости равна 7,9%.

Подобное колебание величины меры изменчивости таксационных признаков имеет общий характер. По данным ряда исследователей, ме­ра изменчивости таксационных признаков для однородных насажде­ний колебалась в следующих пределах: *

Объем дерева, % 40—50

Диаметр дерева на высоте груди, % 20—25

Высота дерева, % 8—43

Коэффициент формы дерева, % 5— 7

Большая изменчивость диаметра и в особенности объема дерева го­ворит о том, что в процессе своего развития дерево может свободно рас­поряжаться пластичностью вещества.

Малая изменчивость высоты, означающая малые 'колебания де­ревьев по высоте, может 'быть объяснена тем, что для обеспечения су-ществов'а,ния необходимо всем деревьям -поднять свою крону возможно выше.

**

Наконец, малая изменчивость коэффициента формы говорит о боль­шой устойчивости относительного сбега ствола. Последнее влечет за со­бой механическую устойчивость растущего дерева, что является исклю­чительно важным для выживания дерева.