
- •Способы получения стандартных случайных чисел. Представление случайных чисел в эвм. Период и отрезок апериодичности датчика случайных чисел.
- •Общий метод моделирования дискретных случайных величин.
- •Модификация метода моделирования дискретных случайных величин с повышенной эффективностью.
- •Общий метод моделирования непрерывных случайных величин.
- •Моделирование кусочно-постоянных непрерывных случайных величин.
- •Метод суперпозиции для дискретного параметра
- •Модифицированный метод суперпозиции с использованием одного случайного числа
- •Метод суперпозиции для непрерывного параметра
- •Метод исключения. Оптимизация.
- •Замена переменных. Использование полярных координат.
- •Моделирование нормального распределения
- •Моделирование обобщенного показательного распределения
- •Общий метод моделирования многомерных распределений
- •Метод исключения для многих переменных
- •Замена переменных в многомерном пространстве. Выбор случайного направления в 3-х мерном пространстве.
- •Общая схема моделирования процесса переноса
- •Моделирование длины свободного пробега в кусочно-однородной среде
- •Метод максимального сечения
- •Моделирование процесса размножения
Метод суперпозиции для непрерывного параметра
Пусть
![]() ,
тогда можно считать, что есть двумерная
плотность.
,
тогда можно считать, что есть двумерная
плотность.
|
1. Моделируем η по плотности
2. Моделируем ξ по плотности
Рассмотрим общий пример: Надо
промоделировать случайную величину
ξ с заданным распределением:
|
|
Вычислим плотность η от у:
![]() ,
а теперь по известной формуле вычислим
,
а теперь по известной формуле вычислим![]()
 .
.
Вычислим плотность (условная вероятность):
![]() .
На втором шаге моделируем
.
На втором шаге моделируем![]() из такого распределения не зависящего
от у:
из такого распределения не зависящего
от у:![]() .
.
Получаем решение:
![]() - задача упростилась, но мы используем
2 случайных числа.
- задача упростилась, но мы используем
2 случайных числа.
|
Итог:
|
Вычисляем
Вычисляем
|

Метод исключения. Оптимизация.
|
|
|
Доказательство:
![]() ,
а η – равномерно распределена от 0 до
,
а η – равномерно распределена от 0 до![]() .
ОбластьGбудет равномерно
заполнена.
.
ОбластьGбудет равномерно
заполнена.
Рассмотрим обратный ход, т.е. область G- равномерно заполнена, значит плотность
совместного распределения![]() ,
если
,
если![]() .
Тогда можно перейти к условным плотностям:
.
Тогда можно перейти к условным плотностям:![]() .
Т.о. верны оба рассуждения.
.
Т.о. верны оба рассуждения.
|
Придумаем для области Gдругую областьG1, которую удобно заполнять.
Будем равномерно заполнять область
G1, при этом некоторые
точки будут равномерно заполнять
областьG, и будем
исключать точки которые областиGне принадлежат: В
этом случае ξ распределено в соответствии
с искомой плотность:
|
|
Шаг 1: равномерно заполняем областьG1.для этого моделируем![]() ,
и с ее помощью моделируем
,
и с ее помощью моделируем![]()
Шаг 2: убираем лишние точки. Если![]() ,
то ξ – искомый ответ, если нет – то нужно
вернутся к первому шагу.
,
то ξ – искомый ответ, если нет – то нужно
вернутся к первому шагу.
Как выбрать функцию
![]() ?
Это мажорирующая функция, и она должна
удовлетворять условиям:
?
Это мажорирующая функция, и она должна
удовлетворять условиям:
1.
![]()
2.
 - легко моделировать в смысле того, что
должен получаться простой и быстрый
алгоритм.
- легко моделировать в смысле того, что
должен получаться простой и быстрый
алгоритм.
3. Не слишком много точек должно быть
выкинуто, т.е. чтобы быстрее получались
нужные точки
![]() должна быть близка к
должна быть близка к![]() -
-![]() близка к 1.
близка к 1.
Основной цикл программы: do{получить
![]() }while
}while![]()
Оптимизация метода исключений.
Введем параметр λ, который будет
приближать g1(x)
кg(x). Пусть
у нас есть неg(x),
а плотность![]() которую необходимо промоделировать,
возьмем плотностьp1(x)
которая имеет более простой вид и
соответственно промоделировать ее
проще.
которую необходимо промоделировать,
возьмем плотностьp1(x)
которая имеет более простой вид и
соответственно промоделировать ее
проще.
В этом случае мы берем не функции, а
плотности. Это значит что площади под
графиками p1(x)
иp(x) равны
единице, а это в свою очередь значит,
чтоp1(x)
не сможет полностью поместить в себеp(x) см.
рисунок. Для этого умножаем нашу плотность
на![]() ,
т.е. на самое большое соотношение между
плотностями (самое большое расстояние
между ними). И при этом берем из возможных
,
т.е. на самое большое соотношение между
плотностями (самое большое расстояние
между ними). И при этом берем из возможных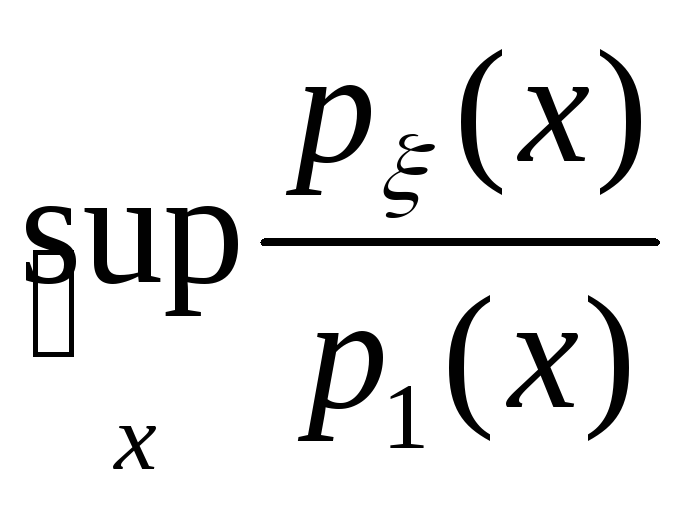 минимальное по
минимальное по![]() для того чтобы соотношение площадей
было максимально приближено к 1 (потому
что когда мы умножаем плотность на этот
супремум она перестаем быть равной 1).
Тогда получаем условие на
для того чтобы соотношение площадей
было максимально приближено к 1 (потому
что когда мы умножаем плотность на этот
супремум она перестаем быть равной 1).
Тогда получаем условие на .
.
|
|
|
Условие оптимизации:

Процесс оптимизации – усложняет мажорирующую функцию, а также создает проблемы с поиском функции и параметра, и следовательно замедляет программу.
Замена переменных. Использование полярных координат.
|
|
η |
ξ |
р |
Пусть есть случайная величина которую
надо промоделировать
|
|
|
|
| ||
|
|
|
| ||
|
|
|
|
![]() .
.
В общем виде: если в 2-х мерном пространстве
есть искомая точка
![]() и мы заменой переменных переходим к
случайной точке
и мы заменой переменных переходим к
случайной точке![]() :
:![]() .
Нужно следить за взаимооднозначностью
преобразований и за монотонностью. Если
.
Нужно следить за взаимооднозначностью
преобразований и за монотонностью. Если![]() не монотонна, то е нужно разбить на
кусочки.
не монотонна, то е нужно разбить на
кусочки.
Рассмотрим случай с полярными координатами.
|
|
полярные координаты |
Подобрать
По
|
Моделируем такие случайные величины,
а потом переходим обратно:
![]() .
.
Получаем
![]() с заданным распределением:
с заданным распределением:








