контрольная по статистике вариант 0

МОСКОВСИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ

ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

ИНСТИТУТ СОВРЕМЕННОГО БИЗНЕСА

ГУМАНИТАРНЫЙ ФАКУЛЬТЕТ

КАФЕДРА «БУХГАЛТЕРСКИЙ УЧЁТ, АУДИТ И ФИНАНСОВЫЙ МЕНЕДЖМЕНТ»

КОНТРОЛЬНАЯ РАБОТА ПО КУРСУ «СТАТИСТИКА»

ВАРИАНТ № 0

СТУДЕНТ ГРУППЫ Д03-100 К.М. РАЗУМОВСКАЯ

ПРЕПОДАВАТЕЛЬ Ю.Ф. СИДОХИН

МОСКВА 2005

Изучение формы статистического распределения

Определение среднего стажа рабочих по всей совокупности рабочих и показателей

вариации.

Распределение рабочих по стажу на предприятии, представленное в табл. 1, проверить на соответствие нормальному закону распределения, используя критерии согласия К.Пирсона, В.Романовича и Л.Колмогорова при уровнях значимости 0,05

Таблица 1

Распределение рабочих по стажу работы на предприятии

Стаж работы, лет (xi)	0-2	2-4	4-6	6-8	8-10	10-12	12 и более
Число рабочих (fi)	6	8	12	24	17	8	5

1. Определение среднего стажа рабочих по всей совокупности рабочих и показателей

вариации.

Логической формулой среднего стажа работы является отношение суммарного числа лет, проработанных рабочими на предприятии, к общему числу рабочих.

Поскольку в интервальном ряду распределения отсутствует сведения об индивидуальном стаже работы, то при расчете используют групповые средние, в качестве которых берут середину каждого интервала разбиения по стажу.

Расчетная формула для определения среднего стажа выглядит следующим образом:

где f_i – число рабочих в каждом интервале.

Наиболее широко применяемыми характеристиками вариации признака в совокупности является дисперсия и среднее квадратичное отклонение.

Для определения дисперсии используют формулу:

Среднеквадратичное отклонение определятся по формуле :

В нашем случае дисперсия и среднеквадратичное отклонение будут равны:

Для оценки однородности совокупности рабочих в отношении стажа работы следует рассчитать коэффициент вариации ():

- совокупность не однородна по стажу работы.

Результаты подробных расчетов представлены в табл. 2

Таблица 2

Определение среднего стажа работы и показатели вариации

Стаж работы, лет (xi)	Число рабочих дней (fi)	Середина интервала (xi)	xi * fi	x - xi	(x - xi)^2 * fi
0-2	6	1	6	6.05	219.615
2-4	8	3	24	4.05	131.22
4-6	12	5	60	2.05	50.43
6-8	24	7	168	0.05	0.06
8-10	17	9	153	-1.95	64.6425
10-12	8	11	88	-3.95	124.82
12 и более	5	13	65	-5,95	177,0125
Итого	80		564		767,8

2. Графическое представление вариационного ряда и определение структурных

средних.

Результаты графической обработки исходных данных показаны на рис. 1 и рис. 2

Подсчитываем коэффициент асимметрии Пирсона.

В качестве показателя асимметрии распределения (As) следует использовать отношение:

Исходя из результатов полученных при вычислении коэффициента асимметрии, асимметрию распределения можно считать незначительной.

2. Для описания эмпирического распределения используем уравнение нормального

распределения:

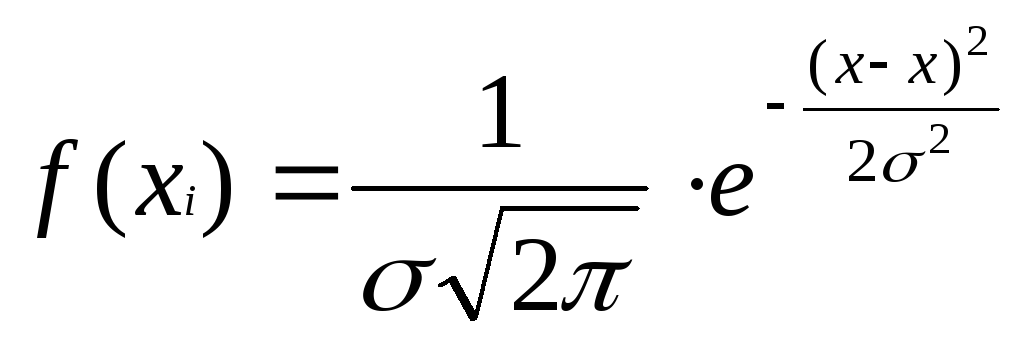
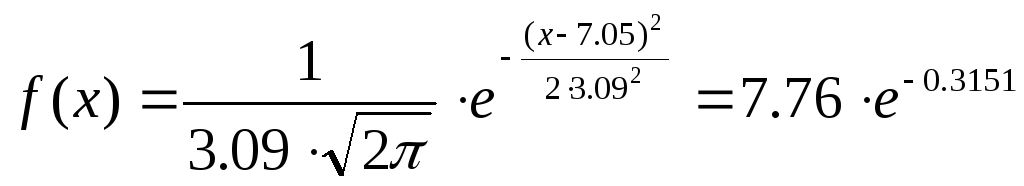
где плотность распределения; x, , - найденные значения среднего стажа работы, дисперсии и среднеквадратичного отклонения, соответствия.

Применение критериев согласия для оценки адекватности принятого теоретического описания распределения (нормальный закон) эмпирическому (гистограмма) требует определение теоретических частот для каждого интервала разбиения совокупности по стажу работы.

Теоретическая частота равна:

где - вероятность попадания рабочих в данный интервал стажа работы. - полное число рабочих.

Вероятность определяется по формуле:

где - нормированная функция Лапласа, значения которой приведены в

Приложении 1;

где и - граничные (минимальный и максимальный) значения стажа работы для каждого интервала.

При расчете вероятностей следует иметь ввиду, что .

Результаты расчетов теоретических частот и вероятностей сведены в табл. 3.

Таблица 3

Расчет критерия согласия Пирсона

Стаж работы, лет	Эмпирические частоты,	Вероятность,	Теоретические частоты,
0-2	6	0,03995	3,196	7,86	2,45
2-4	8	0,1151	9,208	1,45	0,15
4-6	12	0,2034	16,272	18,24	1,12
6-8	24	0,2472	19,776	4,22	0,21
8-10	17	0,21105	16,884	0,01	0,0005
10-12	8	0,11625	9,3	1,69	0,18
12-14	5	0,04225	3,38	2,62	0,77
Итого	80	0,9752	78,016		4,83

В результате суммирования результатов, приведенных в последнем столбце табл. 3, получаем расчетное значение критерия

(- число интервалов (=7))

рассчитанный критерий не превышает максимально возможную величину расхождений эмпирических и теоретических частот, которая может возникнуть в силу случайных колебаний выборочных экспериментальных данных. В этом случае гипотеза о близости эмпирического распределения к нормальному при принятом уровне значимости не отвергается.

2. Используя полученное ранее значение критерия 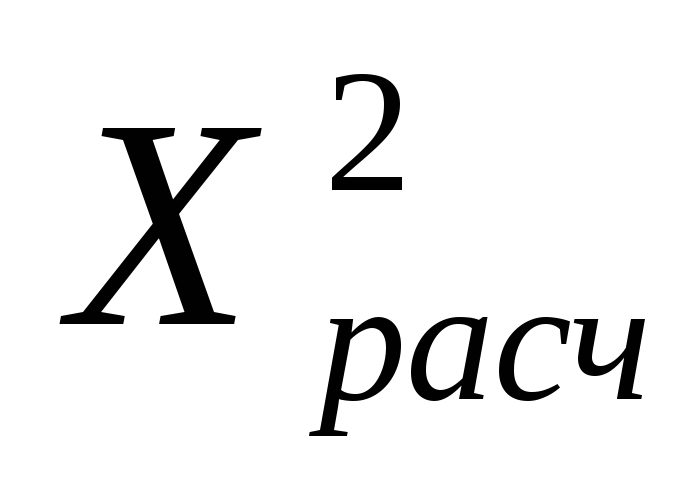применить критерий

согласия В.Романовского:

где K – число степеней свободы.

- гипотеза о нормальном характере распределения принимается.

2. Для применения критерия согласия А.Колмогорова подсчитаем последовательные

накопления экспериментальных частот и теоретических .Установим максимальное значение абсолютной разности накопленных частот в одном из интервалов . Результаты представим в табл. 4.

Таблица 4

Расчет критерия согласия А.Колмогорова

Стаж работы, лет	Частоты		Накопленные частоты
	Эмпирические частоты,	Теоретические частоты,	Эмпирические частоты,	Теоретические частоты,
0-2 2-4 4-6 6-8 8-10 10-12 12 и более	6 8 12 24 17 8 5	3,196 9,208 16,272 19,776 16,884 9,3 3,38	6 14 26 50 67 75 80	3,196 12,404 28,676 48,452 65,336 74,636 78,016	2,804 1,596 2,676 1,548 1,664 0,364 1,984

Критерий согласия А.Колмогорова основан на сопоставлении величины максимальной разности накопленных относительных теоретической и экспериментальной частот:

На основании заданного уровня значимости найдем доверительную вероятность. Вероятность связана с уровнем значимости соотношением:

Так как 0,03<0,15 то с вероятностью 0,95 можно считать, что рассматриваемое распределение соответствует закону нормального распределения.