
- •§10 Термодинамика кристаллов
- •§11 Дебаевское приближение
- •§12 Неустойчивость одномерных и двумерных кристаллов
- •§13 Эффект Мёссбауэра
- •§14 Вероятность эффекта Мёссбауэра
- •§15 Рассеяние тепловых нейтронов на кристалле
- •§16 Когерентное и некогерентное рассеяние. Условие Вульфа-Брэггов
- •§17 Уравнение состояния колеблющегося кристалла
- •§18 Спиновые волны в ферромагнетиках
- •§19 Основное состояние и возбуждение магнонов
- •§20 Термодинамика ферромагнетиков
§14 Вероятность эффекта Мёссбауэра
 Векторный
потенциал поля электромагнитной волны
запишем следующим образом:
Векторный
потенциал поля электромагнитной волны
запишем следующим образом: ;
; ;
;
 Здесь
через
Здесь
через обозначено начальное состояние, а через
обозначено начальное состояние, а через - конечное.
- конечное.


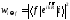 ;
;
 .
Используем выражение для оператора
смещения из §9:
.
Используем выражение для оператора
смещения из §9:


 .
;
.
;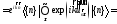

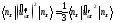 .
.
 (14.1)
(14.1)

Это так называемый фактор Дебая-Уоллера1.

вероятность чисто
упругого поглощения или испускания
кванта
 ;
;
 .
. Теперь
запишем фактор Дебая-Уоллера с помощью
функции плотности частот.
Теперь
запишем фактор Дебая-Уоллера с помощью
функции плотности частот.


предположим, что
температура равна нулю.
 .
.
Значит,
 .
.

 ,
т.е. при нулевой температуре
,
т.е. при нулевой температуре

Температура не
нулевая.

вклад дают лишь
частоты, удовлетворяющие условию:
 .
.
Вычисляем вероятность эффекта.

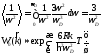
§15 Рассеяние тепловых нейтронов на кристалле
кристалл объёмом
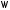 .
Пучок нейтронов предполагается
монохроматическим и коллимированным,
т.е. точно известно направление пучка.
Переданный нейтроном импульс
.
Пучок нейтронов предполагается
монохроматическим и коллимированным,
т.е. точно известно направление пучка.
Переданный нейтроном импульс ,
энергия, переданная нейтроном,
,
энергия, переданная нейтроном, .
Направление движения рассеянного
нейтрона также считается точно известным:
нейтрон улавливается детектором,
расположенным под известным углом. Цель
дальнейших действий такова: определить,
что произошло с нейтроном внутри
кристалла.
.
Направление движения рассеянного
нейтрона также считается точно известным:
нейтрон улавливается детектором,
расположенным под известным углом. Цель
дальнейших действий такова: определить,
что произошло с нейтроном внутри
кристалла.
Начальная волновая
функция нейтрона имеет вид
 .
.
Волновая функция
рассеянного нейтрона
 .
.
 (15.1)
(15.1)
 (15.2)
(15.2)
Здесь
 - начальное и конечное состояние кристалла
как целого.
- начальное и конечное состояние кристалла
как целого.
Если бы для
рассеяния все ядра были тождественны,
то можно было бы записать
 .
.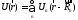
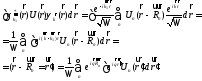

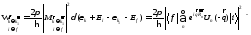


Если обозначить
 гамильтониан кристалла, то
гамильтониан кристалла, то .Комбинация
.Комбинация может быть представлена как
может быть представлена как .
Аналогично
.
Аналогично .
Тогда
.
Тогда
 (15.3)
(15.3)
Связаны операторы
в представлении Шрёдингера и Гейзенберга
соотношением:
 .
.


нужно проводить
усреднение, используя распределение
Гиббса
 .
.
 (15.4)
(15.4)
Двойными угловыми
скобками здесь обозначено усреднение
сначала в квантовомеханическом смысле,
а потом с помощью распределения Гиббса.
Величина
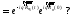 называется корреляционной функцией
ядер.
называется корреляционной функцией
ядер.

Проводим последнее усреднение соотношения (15.4):

Рассмотрим
диагональный матричный элемент
Представим
 ,
тогда
,
тогда


В §14 уже говорилось,
что
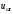 - всегда малая величина
- всегда малая величина

 Рассмотрим
сначала третье слагаемое, считая кристалл
кубическим:
Рассмотрим
сначала третье слагаемое, считая кристалл
кубическим:


Будем завершать вычисление:

введём обозначение
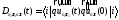


Интеграл первого
слагаемого даст
 ,
а интеграл второго слагаемого –
фурье-образ функции
,
а интеграл второго слагаемого –
фурье-образ функции .
Окончательно получаем:
.
Окончательно получаем:

§16 Когерентное и некогерентное рассеяние. Условие Вульфа-Брэггов

 ,
где
,
где
 - вектор обратной решётки
- вектор обратной решётки

Выражение для
вероятности разделилось на две части:
в первой части присутствует
 ,
во второй -
,
во второй - .
Таким образом, флуктуации оказались во
втором слагаемом. Первая часть называется
когерентной, вторая – некогерентной.
.
Таким образом, флуктуации оказались во
втором слагаемом. Первая часть называется
когерентной, вторая – некогерентной.

 Первое
слагаемое отвечает за упругое рассеяние,
второе – за неупругое.
Первое
слагаемое отвечает за упругое рассеяние,
второе – за неупругое.
Из закона сохранения
энергии следует: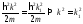
Из закона сохранения импульса:



Это соотношение
называется условием Вульфа-Брэггов.
Условие требует, чтобы угол
 был прямым (см. рис.). Это достижимо только
в том случае, если конец вектора
был прямым (см. рис.). Это достижимо только
в том случае, если конец вектора лежит на границе ячейки.
лежит на границе ячейки.
При вращении
кристалла вектор
 ,
конец которого находился на границе
ячейки, поворачивается. При повороте
на угол
,
конец которого находился на границе
ячейки, поворачивается. При повороте
на угол вектор
вектор имеет возможность восемь раз пересечь
границу ячейки. Момент пересечения
будет соответствовать когерентному
рассеянию. Причём это рассеяние будет
иметь пиковый характер. Исследуя эти
пики, можно узнать геометрию кристалла.
На чертеже также изображён вектор
имеет возможность восемь раз пересечь
границу ячейки. Момент пересечения
будет соответствовать когерентному
рассеянию. Причём это рассеяние будет
иметь пиковый характер. Исследуя эти
пики, можно узнать геометрию кристалла.
На чертеже также изображён вектор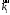 .
Видно, что при достаточно небольшом
повороте вектора
.
Видно, что при достаточно небольшом
повороте вектора вектор
вектор существенно меняется.
существенно меняется.
Переходим к рассмотрению слагаемого, связанного с неупругим рассеянием.

Вычислить нужно
 .
.

Теперь используем выражение для оператора смещения:

С помощью этих выражений продолжаем:






вектор
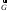 должен быть таким, чтобы вектор
должен быть таким, чтобы вектор попал внутрь ячейки. Причём такое условие
оставляет единственную возможность
выбора вектора
попал внутрь ячейки. Причём такое условие
оставляет единственную возможность
выбора вектора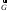 .
.
Вектор
 - период, а потому может быть отброшен
из аргументов в последнем выражении,
учитывая чётность частот:
- период, а потому может быть отброшен
из аргументов в последнем выражении,
учитывая чётность частот: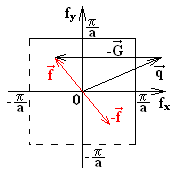

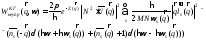


График зависимости
вероятности неупругого когерентного
рассеяния от изменения энергии изображён
рисунке.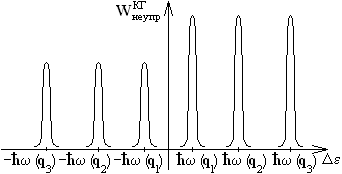


Снова разделим это выражение на две части: упругую и неупругую.



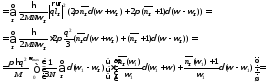
Выражение в квадратных скобках есть функция плотности частот



