§17 Уравнение состояния колеблющегося кристалла

Выражение для свободной энергии Гельмгольца:

;

, ;

:.

.

.

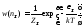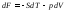Если принять , то

;Теперь вычислим коэффициент теплового расширения кристалла.;

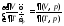
Т.е. получается 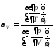.Запишем, где. И это давление является главным. Физически это давление, требуемое для разрушения всех связей в кристалле.

и- полная теплоёмкость, находим

Это утверждение называется законом Грюнайзена.

§18 Спиновые волны в ферромагнетиках

диполь-дипольном взаимодействии. Оценим энергию этого взаимодействия.

Если перевести эту величину в градусы Кельвина, то получится величина порядка одного градуса Кельвина.

Рассмотрим модельную задачу. Имеется два атома, расположенных близко друг к другу. Найдём энергию взаимодействия двух электронов их оболочек. Пространственная часть волновой функции электронов имеет вид:

(18.1)

Знак плюс отвечает симметричной функции, минус – антисимметричнойТак определили, что нужно выбрать в выражении (18.1) знак минус.

- обычный кулоновский потенциал взаимодействия.

(18.2)

, где

Запишем величину A иначе:

Если величина , то при выборе знака минус при ней получим убывание энергии за счёт обменного взаимодействия. за выстраивание моментов отвечает обменное взаимодействие.

Фактически обменное взаимодействие было представлено как взаимодействие между спинами.

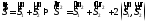
полного спина, равного 1

полного спина, равного 0

необходимо сделать некоторое направление .

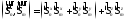, ;, где ;;

, тогда

Окончательно гамильтониан приобретает вид:

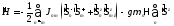
§19 Основное состояние и возбуждение магнонов

Назовём основным состояние .

Двойную сумму первого слагаемого можно свести к простой сумме, если ввести обозначение 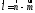и провести суммирование по:

(19.2)

; .

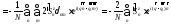
Часть проекций может иметь значение 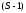. Тогда коммутатор запишется следующим образом:

;. ;

Второе слагаемое в скобках порядка , а потому много меньше1

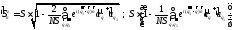
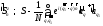
в первом неисчезающем приближении по гамильтониан имеет вид:

, где

Резюме: полная энергия складывается из энергии основного состояния и всегда положительной добавки, связанной с возникновением на узлах решётки отклонения проекции спина на ось аппликат на единицу, причём. Получили закон дисперсии спиновых волн.

§20 Термодинамика ферромагнетиков

. Количество магнонов

.

Т.к. кристалл по предположению кубический, то

, где (20.1)¹

Из этого соотношения видно, что магнитное поле сдвигает отсчёт энергии на величину - в спектре образуется щель

;

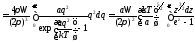
. для фононов.

Теперь случай наличия магнитного поля. Здесь и любая добавка видатолько усилит эту тенденцию. Поэтому пренебрежём: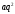

- малая величина.

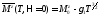
Такое поведение магнитного момента называется законом Блоха. «Включаем» поле.

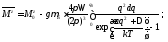
Верхний предел нельзя устремлять к бесконечности, т.к., во-первых, интеграл станет расходящимся, а во-вторых, величина физически не может быть бесконечной. Далее поступаем так же, как и в случае с энергией:

Итак, магнитное поле «держит» магнитный момент, какое-то время не давая ему уменьшаться.

разлагаем экспоненту в ряд:

Что касается пределов интегрирования, то нижний предел нельзя ставить равным нулю, а верхний – бесконечности. Ситуация такая же, как и в §12: нижний предел нужно взять равным некоторому значению и тогда- макроскопическая величина. Включаем поле:

При малейшем нагреве ферромагнетика он теряет свои свойства.

При увеличении температуры отклонения проекций спина на ось аппликат будут возрастать, становясь равными ,и т.д. В системе возникает среднее магнитное поле.

- это мгновенное значение результирующего поля на узле.

(20.1)

Приравняем отношения , найденные двумя способами, введём обозначение:

, где

Функция в правой части называется функцией Ланжевена. Приближение, в рамках которого получено это выражение, называется приближением среднего поля.полагаем 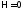, тогда

, где - функция Ланжевена

Левая часть есть просто линейная функция 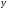. Решать трансцендентное уравнение можно графически. С левой частью всё ясно – это прямая. Угловой коэффициент тем больше, чем больше температура,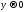

Один корень - - есть всегда Предельное значение углового коэффициента прямой, задаваемой левой частью, отвечает касанию этой прямой кривой, определяемой функцией Ланжевена

Это выражение получается при помощи разложения в ряд функции Ланжевена. Отсюда можно определить критическую температуру:

(20.2)

Если температура меньше температуры Кюри, то есть уже два корня.

Однако число решений можно получить, не обращаясь к графику.

, где

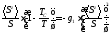(20.3)

И теперь анализируем. Если температура выше температуры Кюри, то левая часть положительна, а правая часть – отрицательна. Тогда равенство (20.3) выполнимо, лишь если . Если же температура ниже температуры Кюри, то

Вблизи температуры Кюри можно заменить в знаменателе на:

Тогда вычисляем магнитный момент (вернее, нам нужен характер температурной зависимости):

Итак, ниже температуры Кюри вещество имеет магнитный момент, т.е. ферромагнитно. Выше температуры Кюри момент пропадает, вещество парамагнитно. Таким образом, в точке, соответствующей температуре Кюри происходит фазовый переход второго рода.

Рассмотрим свободную энергию Гиббса . В окрестности температуры Кюри магнитный момент мал, поэтому можно разложить свободную энергию Гиббса по степеням магнитного момента

Условие минимальности свободной энергии Гиббса эквивалентно условиям:

Первое уравнение имеет два корня: и. Первый корень нас интересует только при отсутствии второго. А второй корень может отсутствовать прии температуре выше температуры Кюри. Значит, при температуре, большей температуры Кюри, упорядоченность моментов отсутствует.

Т.е. при температурах выше температуры Кюри величинаA становится отрицательной. Значит, в точке, отвечающей температуре Кюри, величина A должна менять знак. Поэтому в окрестности температуры Кюри она может быть приближённо записана:(20.4)

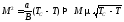(20.5)

В приближении среднего поля получилось то же самое.

1Уоллер указал на то, что не следует вносить множитель ½ в фактор, т.к. его происхождение – разложение экспоненты в ряд

1 Эта формула получится, если вычислить след обеих частей предыдущего равенства

53