Архитектура компьютера - Таненбаум Э

Двоичная арифметика

6 7 3

В системах со знаком и с дополнением до единицы есть два представления нуля: +0 и -0. Такая ситуация нежелательна. В системе с дополнением до двух такой проблемы нет, поскольку здесь плюс нуль это всегда плюс нуль. Но зато в этой системе есть другая особенность. Набор битов, состоящий из 1, за которой следуют все нули, является дополнением самого себя. В результате ряд положительных и отрицательных чисел несимметричен — существует одно отрицательное число без соответствующего ему положительного.

Мы считаем это проблемами, поскольку хотим иметь систему кодировки, в которой:

1.Существует только одно представление нуля.

2.Количество положительных чисел равно количеству отрицательных.

Дело в том, что любой ряд чисел с равным количеством положительных и отрицательных чисел и только одним нулем содержит нечетное число членов, тогда как т битов предполагают четное число битовых комбинаций. В любом случае будет либо одна лишняя битовая комбинация, либо одной комбинации не будет доставать. Лишнюю битовую комбинацию можно использовать для обозначения числа -0, для большого отрицательного числа или для чего-нибудь еще, но она всегда будет создавать неудобства.

Двоичная арифметика

Ниже приведена таблица сложения для двоичных чисел (рис. А.6).

Первое слогаемое	0	0				1 1
Второе слогаемое	_±Р_	_ t l		_±2		_±1
Сумма	0			1	1	0
Перенос	0		0	0		1

Рис. А.6. Таблица сложения для двоичных чисел

Сложение двух двоичных чисел начинается с крайнего правого бита. Суммируются соответствующие биты в первом и втором слагаемом. Перенос совершается на одну позицию влево, как и в десятичной арифметике. В арифметике с дополнением до единицы перенос от сложения крайних левых битов прибавляется к крайнемуправомубиту. Этотпроцесс называется циклическим переносом. В арифметике с дополнением до двух перенос, полученный в результате сложения крайних левых битов, просто отбрасывается. Примеры арифметических действий над двоичными числами показаны на рис. А.7.

Если первое и второе слагаемые имеют противоположные знаки, ошибки переполнения не произойдет. Если они имеют одинаковые знаки, а результат — противоположный знак, значит, произошла ошибка переполнения и результат неверен. И в арифметике с дополнением до единицы, и в арифметике с дополнением до двух переполнение происходит тогда и только тогда, когда перенос в знаковый бит

674 Приложение А. Двоичные числа

отличается от переноса из знакового бита. В большинстве компьютеров перенос из знакового бита сохраняется, но перенос в знаковый бит не виден из ответа, поэтому обычно вводится специальный бит переполнения.

Десятичные	Дополнение	Дополнение
числа	до единицы	ДОдвух
10	00001010	00001010
+ (-3)	11111100	11111101
+7	1 00000110	1I 00000111
	Перенос 1	Отбрасывается

00000111

Рис. А.7. Сложение в системах с дополнением до единицы и с дополнением до двух

Вопросы и задания

1.Преобразуйте следующие числа в двоичные: 1984, 4000, 8192.

2.Преобразуйте двоичное число 1001101001 в десятичную, восьмеричную и шестнадцатеричную системы.

3.Какие из следующих цепочек символов являются шестнадцатеричными числами? BED, CAB, DEAD, DECADE, ACCEDED, BAG, DAD.

4.Выразите десятичное число 100 в системах счисления с основаниями от 2 до 9.

5.Сколько различных положительных целых чисел можно выразить в k разрядах, используя числа с основанием системы счисления г?

6.Большинство людей с помощью пальцев на руках могут сосчитать до 10. Однако компьютерщики способны на большее. Представим, что каждый палец соответствует одному двоичному разряду. Пусть вытянутый палец означает 1, а загнутый — 0. До скольки мы можем сосчитать, используя пальцы обеих рук? А если рассматривать пальцы на руках и на ногах? Представим, что большой палец левой ноги — это знаковый бит для чисел с дополнением до двух. Сколько чисел можно выразить таким способом?

7.Выполните следующие вычисления над 8-битными числами с дополнением до двух:

00101101 11111111 00000000 11110111

+01101111 [phone] -11111111 -11110111

8.Выполните те же вычисления в системе с дополнением до единицы.

9.Ниже приведены задачи на сложение 3-битных двоичных чисел в системе

сдополнением до двух. Для каждой суммы установите:

а. Равен ли знаковый бит результата 1. б. Равны ли младшие три бита 0.

Вопросы и задания

675

в. Не произошло ли переполнения.

000	000	111	100	100
+001	+111	+110	+111	+100

10.Десятичные числа со знаком, состоящие из п разрядов, можно представить в га+1 разрядах без знака. Положительные числа содержат 0 в крайнем левом разряде. Отрицательные числа получаются путем вычитания каждого разряда из 9. Например, отрицательным числом от 014725 будет 985274. Такие числа называются числами с дополнением до девяти. Они аналогичны двоичным числам с дополнениемдо единицы. Выразите следующие числа в виде 3-разрядных чисел в системе с дополнением до девяти: 6, -2, 100, -14, -1, 0.

11.Сформулируйте правило для сложения чисел с дополнением до девяти, а затем выполните следующие вычисления:

0001	0001	9997	9241
+9999	+9998	+9996	+0802

12.Система с дополнением до десяти аналогична системе с дополнением до двух. Отрицательное число в системе с дополнением до десяти получается путем прибавления 1 к соответствующему числу с дополнением до девяти без учета переноса. По какому правилу происходит сложение в системе с дополнением до десяти?

13.Составьте таблицы умножения для чисел системы счисления с основанием 3.

14.Перемножьте двоичные числа 0111 и ООН.

15.Напишите программу, которая на входе получает десятичное число со знаком в виде цепочки ASCII, а на выходе выводит представление этого числа в восьмеричной, шестнадцатеричной и двоичной системе с дополнением до двух.

16.Напишите программу, которая на входе получает 2 цепочки из 32 символов ASCII, содержащие нули и единицы. Каждая цепочка представляет 32-бит- ное двоичное число в системе с дополнением до двух. На выходе программа должна выдавать их сумму в виде цепочки из 32 символов ASCII, содержащей нули и единицы.

Приложение Б

Числа с плавающей точкой

Диапазон чисел, используемых при различных вычислениях, очень велик. Например, в астрономические вычисления может включаться масса электрона (9x1028 граммов) и масса Солнца (2x1033 граммов). Диапазон чисел здесь превышает 1060. Эти числа можно представить следующим образом:

0000000000000000000000000000000000.0000000000000000000000000009

2000000000000000000000000000000000.0000000000000000000000000000

При всех вычислениях должны сохраняться 34 разряда слева от десятичной запятой и 28 разрядов справа от нее. Это даст 62 значимых разряда в результатах. На бинарном компьютере можно использовать арифметику с многократно увеличенной точностью, чтобы обеспечить достаточную значимость. Однако мы не можем определить массу Солнца с точностью даже до пяти значимых разрядов, не говоря уже о 62. В действительности практически невозможно выполнить какиелибо измерения с точностью до 62 знаков. Можно было бы хранить все промежуточные результаты с точностью до 62 значимых разрядов, а перед выводом окончательных результатов отбрасывать 50 или 60 разрядов, но процессор и память тратили бы на это слишком много времени.

Нам нужна такая система для представления чисел, в которой диапазон выражаемых чисел не зависит от числа значимых разрядов. В этом приложении мы расскажем о такой системе. В ее основе лежит экспоненциальное представление чисел, которое применяется в физике, химии и машиностроении.

Принципы представления с плавающей точкой

Числа можно выражать в следующей общепринятой экспоненциальной форме: и=/хЮе

где / называется дробью, или мантиссой, а е (это положительное или отрицательное целое число) называется экспонентой. Компьютерная версия такого представления называется представлением сплавающейточкой. Ниже приведены примеры чисел в такой записи.

3,14 =0,314хЮ1=3,14х10°

0,000001 =0,1хЮ-5=1,0х10-6

1941 = 0,1941х104=1,941х103

Принципы представления с плавающей точкой

677

Область значений определятся по числу разрядов в экспоненте, а точность определяется по числу разрядов в мантиссе. Существует несколько способов представления того или иного числа, поэтому одна форма выбирается в качестве стандартной. Чтобы изучить свойства такого способа представления, рассмотрим представление R с трехразрядной мантиссой со знаком в диапазоне 0,l<|f|<l и двухразрядной экспонентой со знаком. Эти числа находятся в диапазоне от +0,100x10"" до +0,999х10+", то есть простираются почти на 199 значимых разрядов, хотя для записи числа требуется всего 5 разрядов и 2 знака.

Числа с плавающей точкой можно использовать для моделирования системы действительных чисел в математике, хотя здесь есть несколько существенных различий. На рис. Б.1 представлена ось действительных чисел. Она разбита на

7областей:

1.Отрицательные числа меньше -0,999x10".

2.Отрицательные числа от -0,999x10" до -0,100x10"".

3.Отрицательные числа от -0,1ООх 10"" до нуля.

4.Нуль.

5.Положительные числа от 0 до 0,1ООх10"".

6.Положительные числа от 0,100x10"" до 0,999x10".

7.Положительные числа больше 0,999x10".

	3	5
	Отрицательная	Положительная
1	2 П 0 т е Р я значимости 4 потеря значимости g		у
		/	Положительная

	\		Нуль				/		Выражаемые	потеря
						je			отрицательные числа	значимости
	-\		1				1		h
-10"	-10'1 00		0				10"100

Рис. Б. 1. Ось действительных чисел разбита на 7 областей

Первое отличие действительных чисел от чисел с плавающей точкой, которые записываются тремя разрядами в мантиссе и двумя разрядами в экспоненте, состоит в том, что последние нельзя использовать для записи чисел из областей 1,3, 5 и 7. Если в результате арифметической операции получится число из области 1 или 7 (например, 1060х1060=10120), то произойдет ошибка переполнения и результат будет неверным. Причина — ограничение области значений чисел в данном представлении. Точно так же нельзя выразить результат из области 3 или 5. Такая ситуация называется ошибкой из-за потери значимости. Эта ошибка менее серьезна, чем ошибка переполнения, поскольку часто нуль является вполне удовлетворительным приближением для чисел из областей 3 или 5. Остаток счета в банке на 10"102 не сильно отличается от остатка счета 0.

Второе важное отличие чисел с плавающей запятой от действительных чисел — это их плотность. Между любыми двумя действительными числами хну существует другое действительное число независимо от того, насколько близко к у расположен х. Это свойство вытекает из того, что между любыми различными действи-

6 7 8 Приложение Б. Числа с плавающей точкой

тельными числами хну существует действительное число z=(x+y)/2. Действительные числа формируют континуум.

Числа с плавающей точкой континуума не формируют. В двухзнаковой пятиразрядной системе можно выразить ровно 179100 положительных чисел, 179100 отрицательных чисел и 0 (который можно выразить разными способами), то есть всего 358201 чисел. Из бесконечного числа действительных чисел в диапазоне от -10+10° до +0,999x10" в этой системе можно выразить только 358201 число. На рис. Б.1 эти числа показаны точками. Результат вычислений может быть и другим числом, даже если он находится в области 2 или 6. Например, результат деления числа +0,100x103 на 3 нельзя выразить точно в нашей системе представления. Если полученное число нельзя выразить в используемой системе представления, нужно брать ближайшее число, которое представимо в этой системе. Такой процесс называется округлением.

Промежутки между смежными числами, которые можно выразить в представлении с плавающей запятой, во второй и шестой областях не постоянны. Промежуток между числами +0,998x10" и +0,999x10" гораздо больше промежутка между числами +0,998x10° и +0,999x10°. Однако если промежутки между числом и его соседом выразить как процентное отношение от этого числа, большой разницы в промежутках не будет. Другими словами, относительная погрешность, полученная при округлении, приблизительно равна и для малых, и для больших чисел.

Выводы, сделанные для системы представления с трехразрядной мантиссой и двухразрядной экспонентой, справедливы и для других систем представления чисел. При изменении числа разрядов в мантиссе или экспоненте просто сдвигаются границы второй и шестой областей и меняется число представляемых единиц

вэтих областях. С увеличением числа разрядов в мантиссе увеличивается плотность элементов и, следовательно, точность приближений. С увеличением количества разрядов в экспоненте размер областей 2 и 6 увеличивается за счет уменьшения областей 1, 3, 5 и 7. В табл. Б.1 показаны приблизительные границы области 6 для десятичных чисел с плавающей точкой с различным количеством разрядов

вмантиссе и экспоненте.

ТаблицаБ.1. Приблизительныеверхняяинижняяграницычиселсплавающейточкой

	Количество разрядов Количество разрядов		Нижняя			Верхняя
	в мантиссе	в экспоненте	граница			граница
	3	1	ю-12			109
	3	2	Ю-102			10"
	3	3	Ю-1002			1Q999
	3	4	ю-13
	4	1				109
	4	2	10-юз			10"
	4	3	1 Q-1OO3			1Q999
	4	4	Ю-'оооз			Ю9999
	5	1	ю-'4			109
	5	2	Ю-104			10"
	5	3			~ 1 ° 1	1Q999
			1	0		1 П9999
	5	4				1 уаааа
	10	3	1 Q-10O9			Ю 9 "
	20	3	Ю-1019
						1Q999

Принципы представления с плавающей точкой	679

Вариант такого представления применяется в компьютерах. Основа возведения в степень — 2,4,8 или 16, но не 10. В этом случае мантисса состоит из цепочки двоичных, четверичных, восьмеричных и шестнадцатеричных разрядов. Если крайний левый разряд равен 0, все разряды можно сместить на один влево, а экспоненту уменьшить на 1, не меняя при этом значения числа (исключение составляет ситуация потери значимости). Мантисса с ненулевым крайним левым разрядом называется нормализованной.

Нормализованные числа обычно предпочитаются ненормализованным, поскольку существует только одна нормализованная форма, а ненормализованных форм может быть много. Примеры нормализованных чисел с плавающей точкой даны на рис. Б.2. для двух основ возведения в степень. В этих примерах показана 16-битная мантисса (включая знаковый бит) и 7-битная экспонента. Запятая находится слева от крайнего левого бита мантиссы и справа от экспоненты.

Пример 1: Основа возведения в степень2

к

2"2

2~* 2"6

2"8

2"1 0

2' 1 2

2'1 4

2"1 6

l l

2

2

2"5 |

Z7\

2•э-9

2-

2"15

J M I I

I

I

I

I

I

i g

0

1010100

0

0 0 0 0 0 0

0

0 0

0 1

1 0

1

1 = 2 2 0

(1x2"1 2 +1x2-1 3 +1x2"15

о.

Знак Экспонента

+ 1„о-1б\ -лт?

1

+ со смещением

Мантисса: 1x2'1 2 +1x2"13

I

64(84-64=20)

+1x2^ +1x2-«

Дляприведениякнормализованномувидунужносдвинутьмантиссу

го

влево

на

11

битов

и

вычесть

11

из

экспоненты

Z

S j g

0

1 0 0 1 0 0 1

1

1 0 1

1 0 0

0

0

0

0 0 0

0 0

0 = 2 9

( 1 х 2 ' 1

+ 1 х 2 " 2

II

Знак Экспонента

М а н т и с с а :

1 X 2 - W 1 X

2 - 2

+ 1х2"5 ) = 432

5

+ со смещением

,

.

§•

73-64=9

+ 1 х 2

+ 1 х 2

х

Пример2: Основа возведения встепень 16

Щ

16"1

16"2

16"3

16"4

|

/ \

/ \

/Л

/ \

5

3

gra

0

1000101

0000

1011

QOQQ

OQQQ

= 165 (1х 1 6 ^ В И б 4 ) = 432

q о"

Знак Экспонента

,

I*

+ со смещением

Мантисса: 1х16"3+Вх1 б"4

§•

69-64=5

х

Для приведения к нормализованному виду нужно сдвинуть мантиссу

влево на 2 шестнадцатеричных разряда и вычесть 2 из экспоненты

1

|

0

1000011

0001

1011

0000

0000

=163

(1x161+Вх16"2) = 432

||

Знак Экспонента

мантисса: 1х16"1

+Вх1 б"2

q .§.

+ со смещением

а67-64=3

Рис.Б.2. Примерынормализованныхчиселсплавающейточкой

6 8 0 Приложение Б. Числа с плавающей точкой

СтандартIEEE754

До 80-х годов каждый производитель имел свой собственный формат чисел с плавающей точкой. Все они отличались друг от друга. Более того, в некоторых из них арифметические действия выполнялись неправильно, поскольку арифметика с плавающей точкой имеет некоторые тонкости, которые не очевидны для обычного разработчика аппаратного обеспечения.

Чтобы изменить эту ситуацию, в конце 70-х годов IEEE учредил комиссию для стандартизации арифметики с плавающей точкой. Целью было не только дать возможность переносить данные с одного компьютера на другой, но и обеспечить разработчиков аппаратного обеспечения заведомо правильной моделью. В результате получился стандарт IEEE 754 (IEEE, 1985). В настоящее время большинство процессоров (в том числе Intel, SPARC и JVM) содержат команды с плавающей точкой, которые соответствуют этому стандарту. В отличие от многих стандартов, которые представляли собой неудачные компромиссы и мало кого устраивали, этот стандарт неплох, в большей степени благодаря тому, что его изначально разрабатывал один человек, профессор математики университета Беркли Вильям Каган (William Kahan). Этот стандарт будет описан ниже.

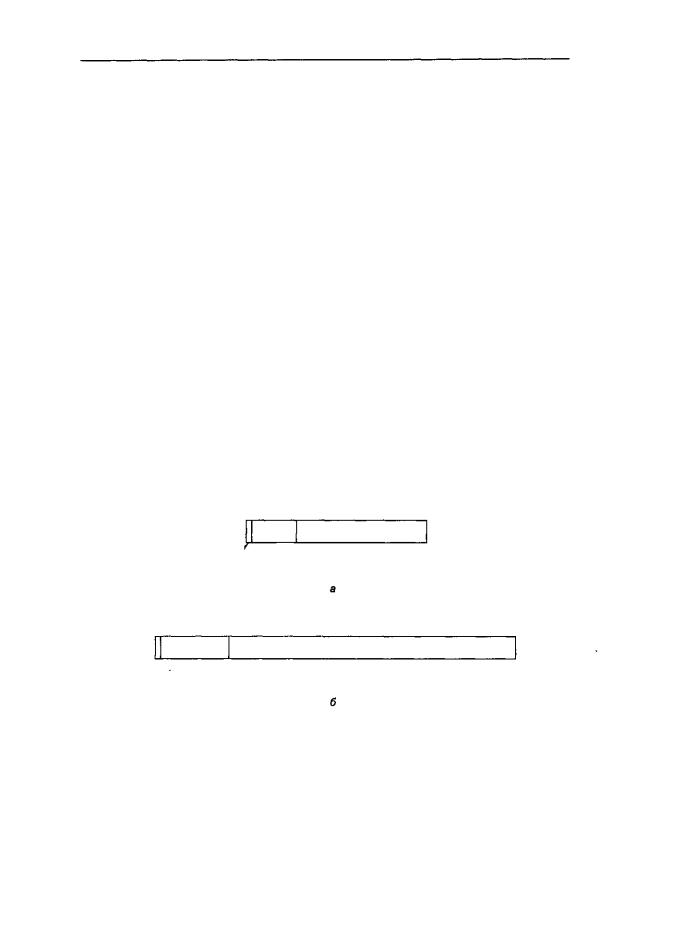
Стандарт определяет три формата: с одинарной точностью (32 бита), с удвоенной точностью (64 бита) и с повышенной точностью (80 битов). Формат с повышенной точностью предназначен для сокращения ошибок округления. Он применяется главным образом в арифметических устройствах с плавающей точкой, поэтому мы не будем о нем говорить. В форматах с одинарной и удвоенной точностью применяется основание возведения в степень 2 для мантисс и смещенная экспонента. Форматы представлены на рис. Б.З.

Биты 1 8	23
	Мантисса

Зн^к ^Экспонента

Биты 1 1 1	5 2
Экспонента	Мантисса
х
Знак

Рис. Б.З. Форматы для стандарта IEEE с плавающей точкой: одинарная точность (а); удвоеннаяточность(б)

Оба формата начинаются со знакового бита для всего числа; 0 указывает на положительное число, а 1 — на отрицательное. Затем следует смещенная экспонента. Для формата одинарной точности смещение (excess) 127, а для формата удвоенной точности смещение 1023. Минимальная (0) и максимальная (255 и 2047)

СтандартIEEE754 681

экспоненты не используются для нормализованных чисел. У них есть специальное предназначение, о котором мы поговорим ниже. В конце идут мантиссы по 23 и 52 бита соответственно.

Нормализованная мантисса начинается с двоичной запятой, за которой следует 1 бит, а затем остаток мантиссы. Следуя практике, начатой с компьютера PDP-11, компьютерщики осознали, что 1 бит перед мантиссой сохранять не нужно, поскольку можно просто предполагать, что он есть. Следовательно, стандарт определяет мантиссу следующим образом. Она состоит из неявного бита, который всегда равен 1, неявной двоичной запятой, за которыми идут 23 или 52 произвольных бита. Если все 23 или 52 бита мантиссы равны 0, то мантисса имеет значение 1,0. Если все биты мантиссы равны 1, то числовое значение мантиссы немного меньше, чем 2,0. Во избежание путаницы в английском языке для обозначения комбинации из неявного бита, неявной двоичной запятой и 23 или 52 явных битов вместо термина «мантисса» (mantissa) используется термин significand. Все нормализованные числа имеют significand s в диапазоне l<s<2.

Числовые характеристики стандарта IEEE для чисел с плавающей точкой даны в табл. Б.2. В качестве примеров рассмотрим числа 0,5,1 и 1,5 в нормализованном формате с одинарной точностью. Они представлены шестнадцатеричными числами 3F000000, 3F800000 и 3FC00000 соответственно.

ТаблицаБ.2.ХарактеристикичиселсплавающейточкойстандартаIEEE

Параметр

Одинарная точность Удвоенная точность

Количествобитоввзнаке Количество битов в экспоненте Количествобитоввмантиссе Общеечислобитов Смещение экспоненты Область значений экспоненты

Самое маленькое нормализованное число Самоебольшоенормализованноечисло Диапазон десятичных дробей Самое маленькое ненормализованное число

1	1
8	11
23	52
32	64
Смещение (excess) 127	Смещение (excess) 1023
От-126 до+127	от-1022до+1023
2-126	2-Ю22
=21 2 8	_21°24
= 1 0 - м д о 1 0 3 8	И О"308 до 103 0 8
=ю-4 5	«ю-3 2 4

Традиционные проблемы, связанные с числами с плавающей точкой, — что делать с переполнением, потерей значимости и неинициализированными числами. Подход, используемый в стандарте IEEE, отчасти заимствован от машины CDC 6600. Помимо нормализованных чисел в стандарте предусмотрено еще 4 типа чисел (рис. Б.4).

Проблема возникает в том случае, если абсолютное значение (модуль) результата меньше самого маленького нормализованного числа с плавающей точкой, которое можно представить в этой системе. Раньше аппаратное обеспечение действовало одним из двух способов: либо устанавливало результат на 0, либо вызывало ошибку из-за потери значимости. Ни один из этихдвух способов не является удовлетворительным, поэтому в стандарт IEEE введены ненормализованные числа. Эти числа имеют экспоненту 0 и мантиссу, представленную следующими 23 или

682 Приложение Б. Числа с плавающей точкой

52 битами. Неявный бит 1 слева от двоичной запятой превращается в 0. Ненормализованные числа можно легко отличить от нормализованных, поскольку у последних не может быть экспоненты 0.

	Нормализованное	±	0 < Ехр < Мах	Любой наборбитов
	число
	Ненормализованное	±	0	Любой нулевой набор битов
	число
	Нуль	±	0	0
	Бесконечность	±	1 1 1...1	0
	Не число	±	1 1 1...1	Любой нулевой набор битов
		\	Знаковый бит

Рис. Б.4. Числовые типы стандарта IEEE

Самое маленькое нормализованное число с одинарной точностью содержит 1 в экспоненте и 0 в мантиссе и представляет 1,0х2~126. Самое большое ненормализованное число содержит 0 в экспоненте и все единицы в мантиссе и представляет примерно 0,9999999х2~127, то есть почти то же самое число. Следует отметить, что это число содержит только 23 бита значимости, а все нормализованные числа — 24 бита.

По мере уменьшения результата при дальнейших вычислениях экспонента попрежнему остается равной 0, а первые несколько битов мантиссы превращаются в нули, что сокращаетизначение, и числозначимыхбитов мантиссы. Самое маленькое ненулевое ненормализованное содержит 1 в крайнем правом бите, а все остальные биты равны 0. Экспонента представляет 2~127, а мантисса — 2 23, поэтому значение равно 2~150. Такая схема предусматривает постепенное исчезновение значимых разрядов, а не перескакивает на 0, когда результат нельзя выразить в виде нормализованного числа.

В этой схеме присутствуют 2 нуля, положительный и отрицательный, определяемые по знаковому биту. Оба имеют экспоненту 0 и мантиссу 0. Здесь тоже бит слева от двоичной запятой по умолчанию 0, а не 1.

С переполнением нельзя справиться постепенно. Вместо этого существует специальное представление бесконечности: с экспонентой, содержащей все единицы, и мантиссой, равной 0. Это число можно использовать в качестве операнда. Оно подчиняется обычным математическим правилам для бесконечности. Например, бесконечность и любое число в сумме дают бесконечность. Конечное число разделить на бесконечность равно 0. Любое конечное число, разделенное на 0, стремится к бесконечности.

А что получится, если бесконечность разделить на бесконечность? Результат не определен. Для такого случая существует другой специальный формат, NaN (Not a Number — не число). Его тоже можно использовать в качестве операнда.