1. Решение прямой и обратной задачи кинематики

В робототехнике, есть две основные задачи кинематики: прямая и обратная.

Прямая задача — это вычисление положения (Xp, Yp, Zp) рабочего органа манипулятора по его кинематической схеме и значениях обобщенных координат (q₁,q₂…q_n) , где n — число степеней свободы манипулятора,q— обобщенные координаты.

Обратная задача — это вычисление величин обобщенных координат (q₁,q₂…q_n) по заданному положению (Xp, Yp, Zp) рабочего органа при известной схеме кинематики манипулятора.

Таким образом, решение прямой задачи говорит о том, где будет находиться рабочий орган манипулятора, при заданных углах его суставов, а обратная задача — как нужно «вывернуться» манипулятору, чтобы его рабочий орган оказался в заданном положении.

Прямую и обратную задачи кинематики манипулятора будем решать геометрически. Кинематическая схема манипулятора, обобщенные координаты его звеньев q_n, их длины l_nизображены на рисунке 1.

Прямая задача. По заданным обобщенным координатам найти положение точки P схвата.

;

;

.

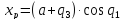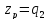Обратная задача. По заданному положению точки P схвата найти обобщенные координаты.

);

;

.

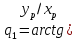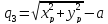2. Исследование динамических свойств манипулятора

Составим расчетную схему (рис. 2) для построения динамической модели, с изображенными силами действия приводов, силами трения и обобщенными координатами.

Манипулятор представляет собой механизм с несколькими степенями свободы с голономными связями, потому воспользуемся уравнениями Лагранжа второго рода для составления уравнений движения.

Уравнения Лагранжа второго рода применительно к исследуемой манипуляционной системе примут вид

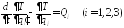. (1)

Кинетическая энергия системы при неподвижном основании определится по формуле:

(2)

где T₁,T₂,T₃ — кинетические энергии звеньев 1, 2, 3 соответственно.

Составим расчетную схему для построения динамической модели, с изображенными силами действия приводов, силами трения и обобщенными координатами.

Рис. 2. Расчетная схема

Так как звено 1 совершает вращательное движение вокруг оси Z, то получаем:

. (3)

Звено 2 совершает пространственное поступательное движение по осям X, Y, Z, то получаем:

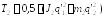_.(4)

Звено 3 совершает пространственное поступательное движение по осям X, Y, Z, то получаем:

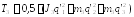_.(5)

Подставляя результаты (3), (4) и (5), получаем

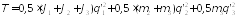_.(6)

Будем считать, что звенья имеют форму цилиндра. Момент инерции звена 1 вокруг неподвижной оси z:

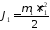(7)

_где r₁-радиус сечения цилиндра звена 1

Момент инерции звена 2 вокруг неподвижной оси zскладывается из суммы моментов инерции частей c1, c2 и c3 и c4 (рис. 3). Учитывая, что масса звена распределена равномерно на каждом участке длины, уравнения для нахождения момента инерции частей звена 3 запишутся следующем образом:

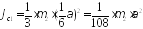(8)

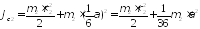(9)

_где r₂-радиус сечения цилиндра звена 2

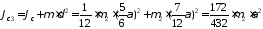(10)

_где d-расстояние между осью вращения и центром с3

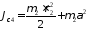(11)

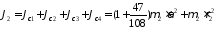(12)

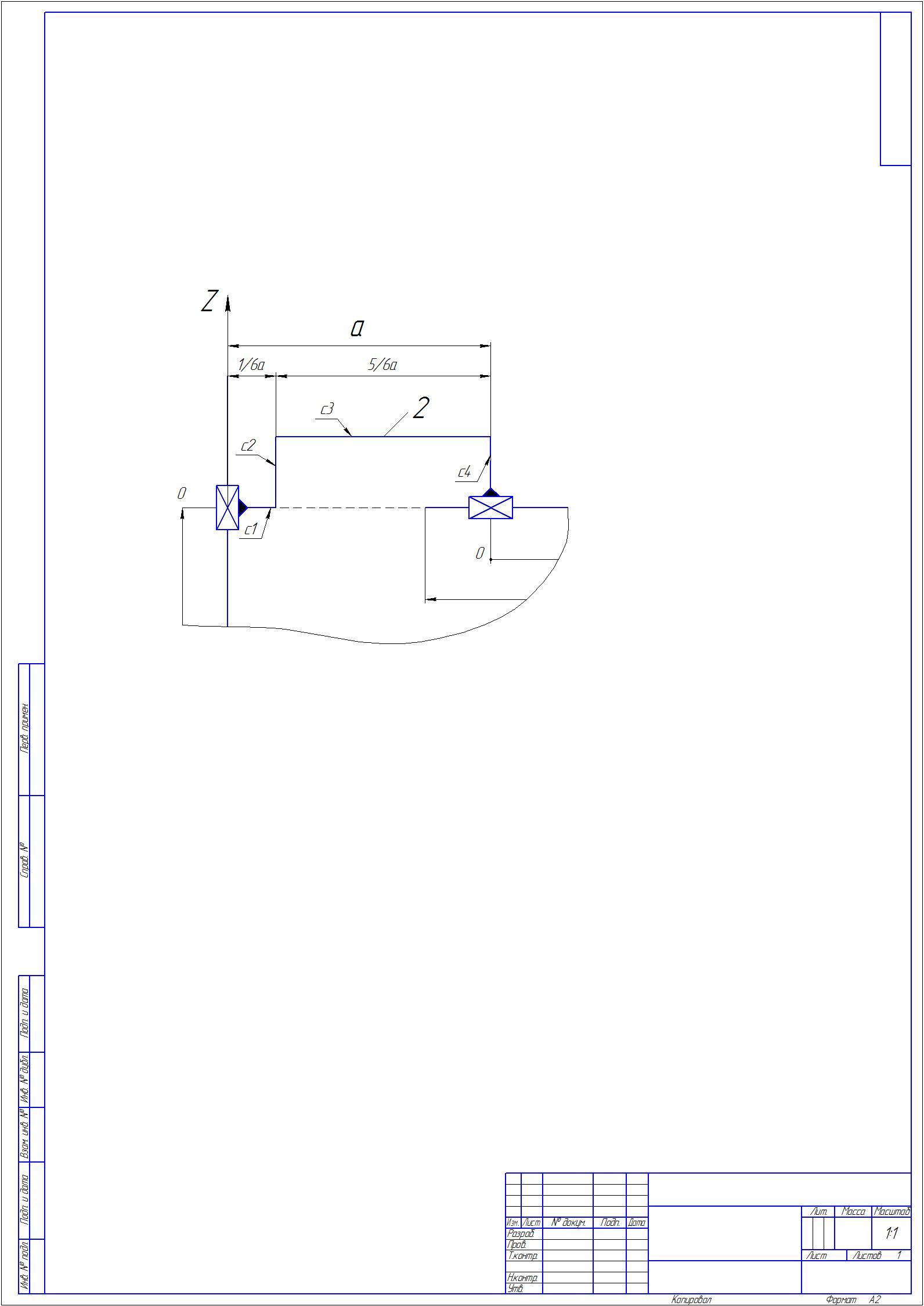
Рис.3. Звено 2 манипулятора

Момент инерции звена 3 вокруг неподвижной оси z:

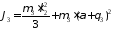(13)

Для вычисления обобщенной силы Q_i, соответствующей обобщенной координатеq_i, поступают следующим образом: сообщают системе такое виртуальное перемещение, при котором изменяется только эта координата q_i, а все остальные координаты остаются неизменными, и вычисляют виртуальную работу всех активных сил на этом перемещении. Тогда множитель при вариации δq_iв полученном выражении виртуальной работы δА_j=Q_iδq_i и будет обобщенной силой Q_i , т. е.

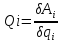; (14)

Изобразим манипулятор в произвольный момент времени и сообщим системе такое виртуальное перемещение, при котором изменяется только обобщенная координата q₁ (рис. 4), которая имеет приращение δq_1.

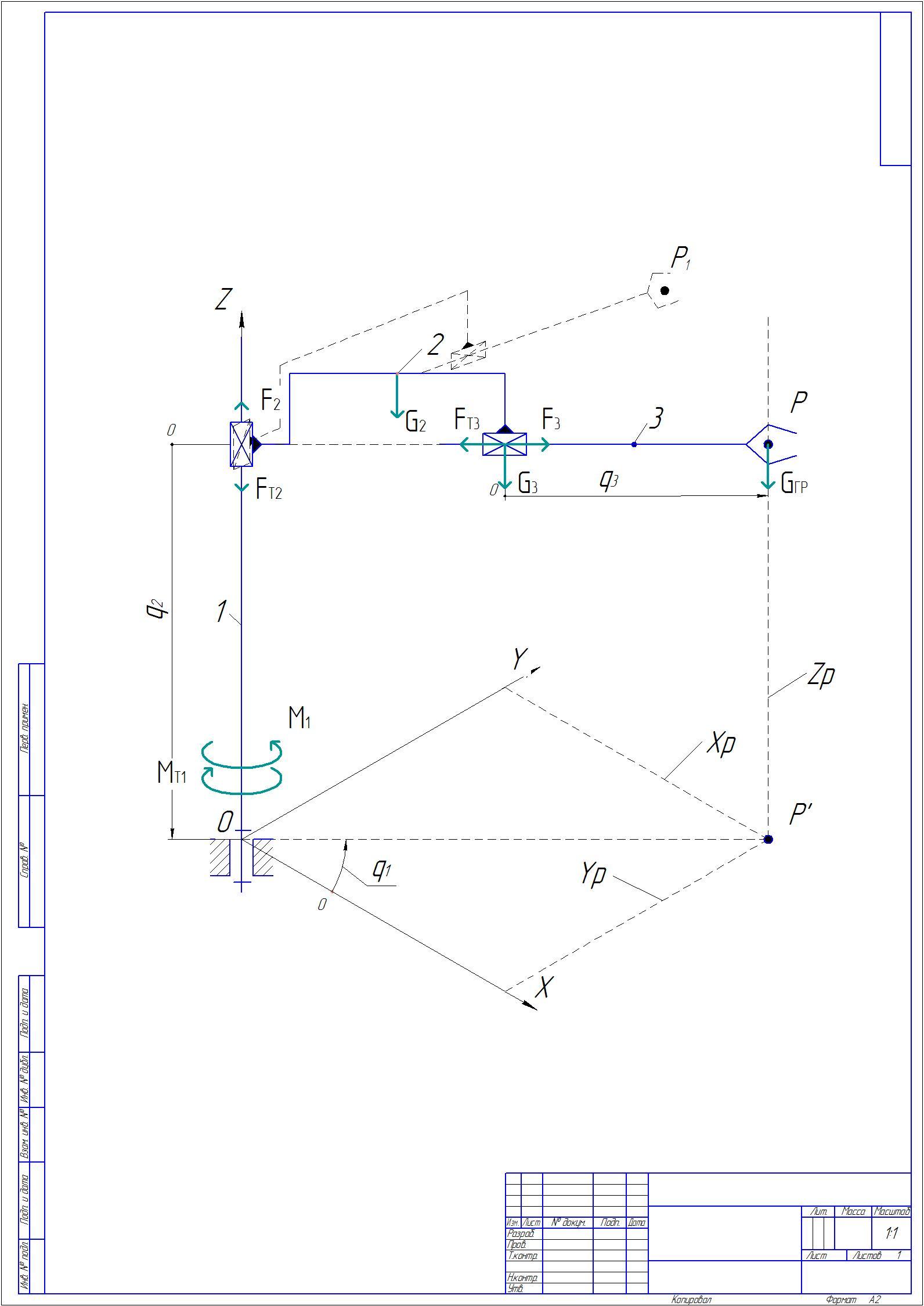
Рис. 4. Изменение обобщенной координаты q₁

При этом точка P превратится вP₁. Вычислим виртуальную работу всех активных сил на этом перемещении:

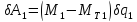; (15)

Множитель при вариации δq₂ в полученном выражении виртуальной работы и будет обобщенной силой Q₂:

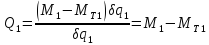; (16)

Изобразим манипулятор в произвольный момент времени и сообщим системе такое виртуальное перемещение, при котором изменяется только обобщенная координата q₂ (рис. 5), которая имеет приращение δq_2.

Рис. 5. Изменение обобщенной координаты q₂

При этом точка P превратится вP₂. Вычислим виртуальную работу всех активных сил на этом перемещении:

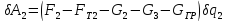. (17)

Множитель при вариации δq₂ в полученном выражении виртуальной работы и будет обобщенной силой Q₂:

. (18)

Изобразим манипулятор в произвольный момент времени и сообщим системе такое виртуальное перемещение, при котором изменяется только обобщенная координата q₃ (рис. 6), которая имеет приращение δq_3.

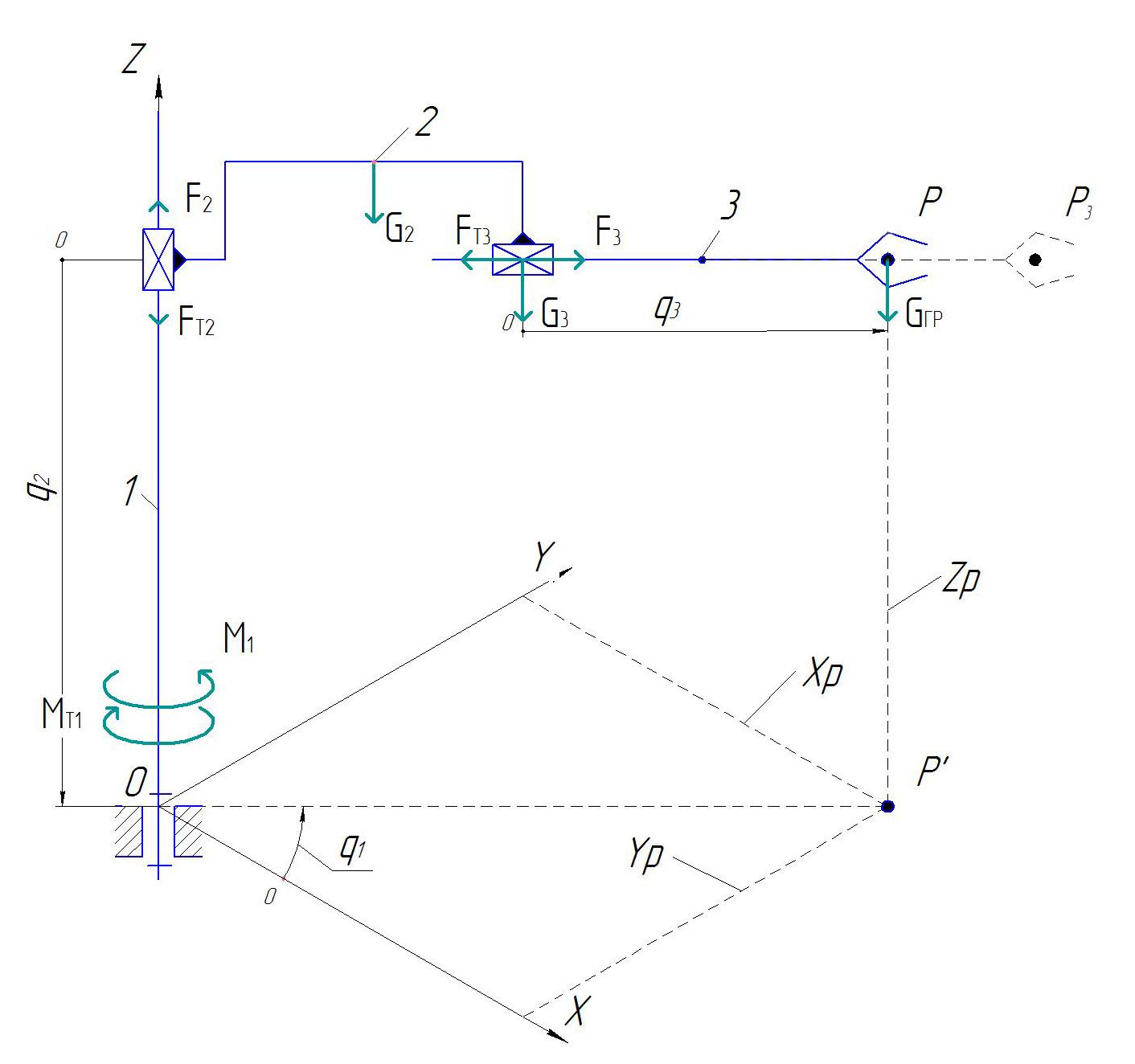
Рис. 6. Изменение обобщенной координаты q₃

При этом точка P превратится вP₃. Вычислим виртуальную работу всех активных сил на этом перемещении:

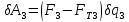; (19)

Множитель при вариации δq₂ в полученном выражении виртуальной работы и будет обобщенной силой Q₂:

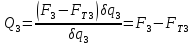. (20) где М₁ — момент силы привода, действующий на звено 1; М_Т1 — момент сил трения, действующий на звено 1; F₃— сила привода, действующая на звено 3; F_Т3— сила трения при движении по осям звена 3;G₂,G₃,G_ГР— силы тяжести, действующие соответственно на звено 2, 3 и груз.

Определим частные производные от кинетической энергии по обобщенным координатам и обобщенным скоростям:

;;

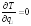;;(21)

;.

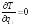Подставляя полученные значения в уравнения Лагранжа (1), получим:

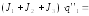M₁ −M_Т1;

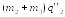=F_Т2−F₂−G₂−G₃; (22)

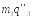= F₃−F_Т3.

Если в задаче требуется найти движение системы, то интегрируют уравнения Лагранжа и определяют по начальным условиям произвольные постоянные интегрирования.

Если в задаче требуется найти неизвестные активные силы, то их определяют из уравнений Лагранжа.

Если в задаче требуется определить неизвестные реакции, то после нахождения из уравнений Лагранжа следует применить принцип освобождаемости к соответствующим телам системы и воспользоваться основным уравнением динамики, либо принципом Даламбера, либо общим уравнением динамики.