ИДЗ (Венгерские методы)

2

Липецкий государственный технический университет

Кафедра автоматизированных систем управления

Индивидуальное домашнее задание

по Теории принятия решений

Задача о назначениях. Венгерский метод

Студент

Ключанских А.С

^подпись, дата

^фамилия, инициалы

Группа

АС-10

Принял

доцент

Корнеев А.М.

^ученая степень, звание

^подпись, дата

^фамилия, инициалы

Липецк 2013

1. Задание

Решить задачу о назначениях:

1. Венгерским методом максимизации (алгоритмы №1 и №2)

2. Венгерским методом минимизации.

2. Решение

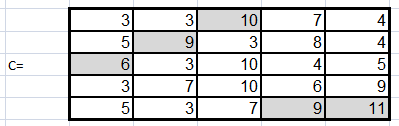
Вариант 10		Работы
Работники		3	3	10	7	4
		5	9	3	8	4
		6	3	10	4	5
		3	7	10	6	9
		5	3	7	9	11

1) Решим задачу о назначениях Венгерским методом минимизации.

Найдем в каждой строке минимальную стоимость:

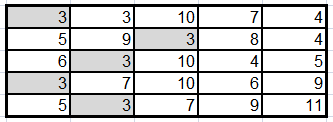
Вычтем из каждого элемента строки минимальную стоимость и найдем в каждом столбце минимальную стоимость:

Вычтем из каждого элемента столбца минимальную стоимость:

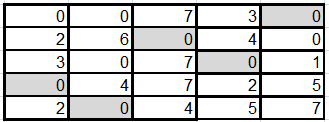
Данное решение является допустимым, оптимальные назначения соответствуют нулевым элементам.

Значит, оптимальные назначения имеют вид:

3	3	10	7	4
5	9	3	8	4
6	3	10	4	5
3	7	10	6	9
5	3	7	9	11

Таким образом, значение функции:.

2) Решим задачу Венгерским методом максимизации (алгоритм №1)

Предварительный этап.

Ищем максимальный элемент в каждом столбце и все элементы этого столбца последовательно вычитаем из максимального. Эту операцию проделываем над всеми столбцами матрицы. Получим матрицу С’

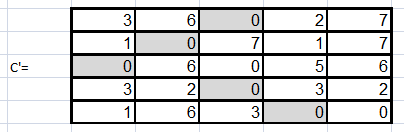
Далее рассматриваем каждую строку полученной матрицы, разыскиваем ее минимальный элемент и из каждого элемента этой строки вычитаем минимальный. Эту процедуру повторяют со всеми строками. В результате получим матрицу С_0.

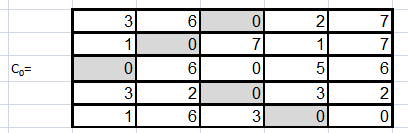
Находим произвольный нуль в первом столбце и отмечаем его звездочкой. Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет нуля со звездочкой, то отмечаем его звездочкой. Аналогично просматриваем один за другим все столбцы матрицы С₀ и отмечаем, если возможно, следующие нули знаком ‘*’. Очевидно, что нули матрицы С₀, отмеченные звездочкой, являются независимыми. На этом предварительный этап заканчивается.

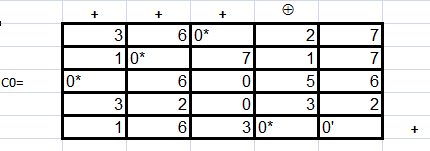
Итерация 1.

Просматриваем 5 столбец на наличие в нем невыделенных нулей. Такой нуль есть, отметим данный нуль штрихом, строку знаком +, и снимем знак выделения с 4 столбца, т.к. там в последней строке имеется нуль со звездочкой. Други нулей в этом столбце нет. Переходим к третьему этапу. h=1. Вычитаем этот элемент из всех невыделенных строк и прибавляем ко всем невыделенным столбцам. Получим матрицу

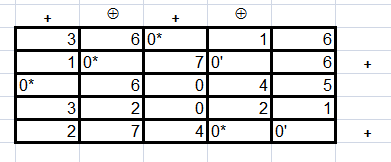
Проделывая аналогичные процедуры снова перейдем к третьему этапу, h=1. Получим матрицу

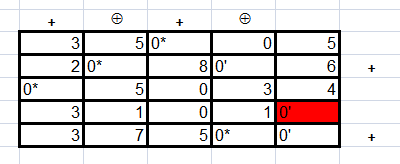
В 4 строке 5 столбца найден нуль, который расположен в строке, не содержащей нуля со звездочкой. Переходим ко второму этапу и строим цепочку. В данном случае она состоит из одного элемента. Меняем этот нуль со штрихом на нуль со звездочкой и получаем в сумме 5 нулей со звездочкой, значит решение найдено. Значение целевой функции: f=6+9+10+9+9=43.

3) Решим данную задачу Венгерским методом максимизации алгоритмом №2.

Исходная матрица представляет собой матрицу отрицательных чисел, по абсолютной величине равных данным по варианту.

В каждой строке таблицы найдем наименьший элемент и вычтем его из всех элементов данной строки. Повторим ту же самую процедуру для столбцов.

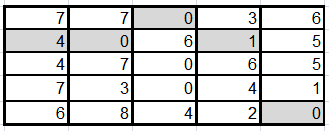
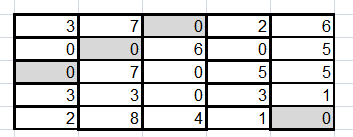
Найдем строки и столбцы, в которых только по одному нулю, выделим данные нули и зачеркнем соответствующие строки (столбцы). Повторим процедуру до тех пор, пока это возможно.

Оптимальное решение не получено, среди невычеркнутых элементов ищем минимальный, вычтем его из всех элементов, через которые не проходят прямые и прибавим его к элементам, расположенным на пересечении прямых. Получим:

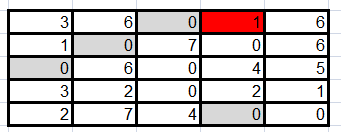
Повторим описанные действия до получения оптимального решения:

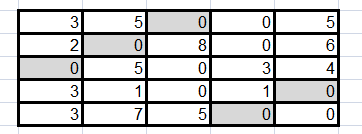
Таким образом, значение целевой функции: f=6+9+10+9+9=43.