6.4 Ранговая корреляция

6.4.1 Условия применения ранговых коэффициентов корреляции:Метрическая или ранговая шкала, Связь между переменными монотонна (не меняет знак). Обязательным условием использования коэффициента Спирмена является равенство размаха двух переменных.

Перед использованием коэффициента Спирмена для рядов данных с различным размахом, необходимо обязательно их ранжировать. Ранжирование приводит к тому, что значения этих рядов приобретают одинаковый минимум = 1 (минимальный ранг) и максимум, равный количеству значений (максимальный, последний ранг =, т.е. максимальному количеству случаев в выборке).

Для расчета коэффициента ранговой корреляции Спирмена используется формула:

.

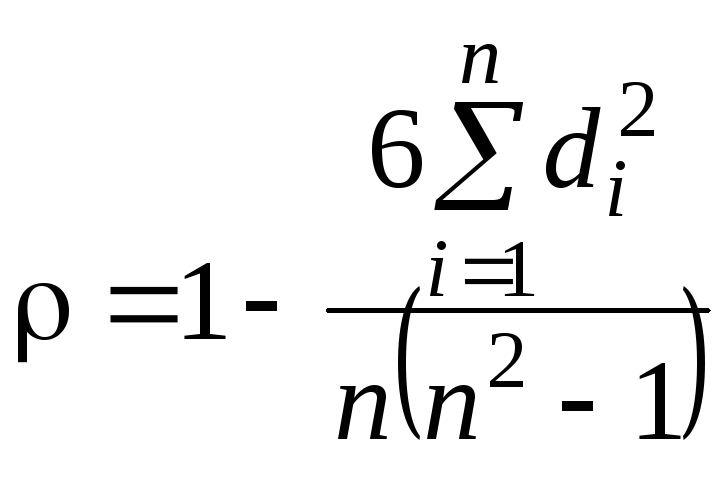Коэффициент рангов Спирмена подтверждает присутствие монотонно-возрастающей или убывающей зависимости (не обязательно линейной).

Проверка нулевой гипотезы об отсутствии статистически значимой связи можно проверить:

1. Путем сравнения критического и эмпирического значений коэффициента ранговой корреляции. Если 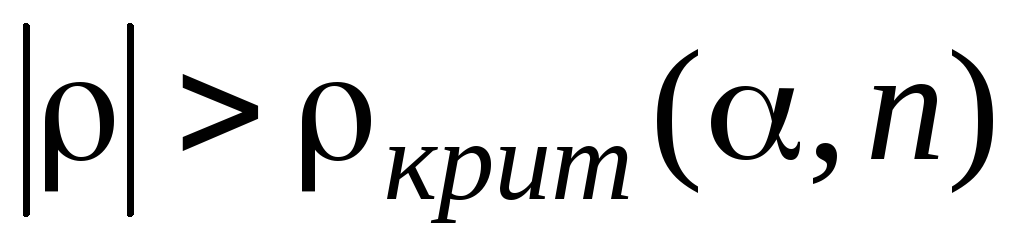, нулевая гипотеза отвергается и можно сделать вывод о существенности связи.

2. На основании -критерия:

,

Если , то нулевая гипотеза об отсутствии корреляционной зависимости между выборками отвергается.

6.4.2 Пример расчета рангового коэффициента корреляции Спирмена

Задача: на основании наблюдений за развивающимся сайтом и изменением его средневзвешенной позиции по основным запросам в поисковой системе необходимо проверить, можно ли говорить о линейной зависимости между позицией сайта и числом посетителей. Исходные данные: (число посетителей в сутки),(усредненная позиция сайта в поисковой системе).

Каждый из элементов признаков (и) ранжируется в порядке возрастания значений, в результате получаются рангии.

Результаты ранжирования представлены в таблице:

n					разность рангов
1	500	4	5,4	6	-2	4
2	790	5	4,2	5	0	0
3	870	6	4,0	4	2	4
4	1500	7	3,4	3	4	16
5	2300	8	2,5	2	6	36
6	5600	9	1,0	1	8	64
7	100	3	6,1	7	-4	16
8	20	2	8,2	8	-6	36
9	5	1	14,6	9	-8	64

Кроме рангов, в таблице рассчитаны разность рангов и квадрат разности рангов пары соответствующих элементов и.

Коэффициент ранговой корреляции Спирмена равен:

Критическое значение для уровня значимости 5% и объема выборки составляет. Так как, нулевая гипотеза отвергается и можно сделать вывод о существенности связи.

Кроме того, можно оценить значение коэффициента корреляции Спирмена на основании -критерия:

,

Следовательно, нулевая гипотеза об отсутствии корреляционной зависимости между выборками отвергается. Обратная связь между числом посетителей сайта и его позицией в поисковой системе является статистически значимой.

5. Множественная корреляция

Изучается степень тесноты линейной связи между k случайными величинами Х1, Х2, …, Хn. Выборка представляется в виде матрицы X, состоящей из результатов n наблюдений за каждым из k элементов случайного вектора:

Размерность этой матрицы n × k: n строк, k столбцов. В первом столбце представлены n значений случайной величины X1 во втором – n значений X2 и т. д.

По этим данным можно построить:

• ковариационную матрицу:

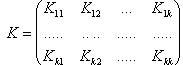, (4.6)

где

на диагонали находятся – дисперсии соответствующей случайной величиныХi,.

• корреляционную матрицу – симметричную с единичными диагональными элементами. Недиагональные элементы этой матрицы – это выборочные коэффициенты парной корреляции, определяемые как

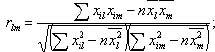
здесь l = 1, …, k; m = 1, …, k; i = 1, …, n.

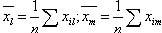
–результат i-го наблюдения за случайной величиной X.

Коэффициенты парной корреляции при множественной корреляции могут привести к неправильным выводам при изучении тесноты связи между двумя случайными величинами Xl и Xm, так как на связь между этими двумя величинами могут оказывать влияние и другие компоненты k-мерного случайного вектора.

Для исключения влияния других случайных величин определяют частный коэффициент корреляции, показывающий меру взаимосвязи между двумя величинами при исключении влияния других. Частный коэффициент корреляции выражается через элементы корреляционной матрицы R. Например, частный коэффициент корреляции между случайными величинами X1 и X2 равен

,

где Rlm – алгебраическое дополнение элемента rlm корреляционной матрицы R. Алгебраическим дополнением элемента rlm называется определитель, получаемый из определителя матрицы R вычеркиванием l-ой строки и m-ого столбца, умноженный на

Значимость частных и парных коэффициентов корреляции, т.е. гипотеза , проверяется по t-критерию Стьюдента. Наблюдаемое значение критерия находится по формуле

где — соответственно оценка частного или парного коэффициента корреляции; k — порядок частного коэффициента корреляции, т.е. число фиксируемых факторов (для парного коэффициента корреляции k=0).

считается значимым, если .

Множественный коэффициент корреляции характеризует тесноту связи между одной переменной (результативной) и остальными, входящими в k-мерный вектор. Если, например, результативной является случайная величина X1, то множественный коэффициент корреляции есть

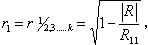
где |R| – определитель корреляционной матрицы.

Квадрат множественного коэффициента корреляции называется коэффициентом детерминации.

Если 12 = 1, то величина X1 является линейной комбинацией случайных величин Х2, Х3, …, Хn. Если же r12 = 0, то величина X1 не коррелирована ни с одной из случайных величин Х2, Х3, …, Хn Чем лучше X1приближается линейными комбинациями Х2, Х3, …, Хn, тем ближе коэффициент детерминации к единице. Значимость парных коэффициентов корреляции определяется с использованием статистики Стъюдента.

По аналогии проверяется значимость частных коэффициентов корреляции; для этого используется статистика

;

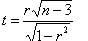(здесь r – соответствующий частный коэффициент корреляции), имеющая распределение Стъюдента с числом степеней свободы (n – 3).

Для проверки значимости коэффициента детерминации используется критерий Фишера. Выборочное значение статистики

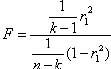
сравнивается с критическим значением, зависящим от уровня значимости, вида альтернативной гипотезы и чисел степеней свободы (k – 1) и (n – k).