ТЕМА 5 ИТЕРАЦИОННЫЕ МЕТОДЫ НАХОЖДЕНИЯ СОБСТВЕННЫХ

ЗНАЧЕНИЙ И ВЕКТОРОВ

5.1. Характеристика итерационных методов

Большинство итерационных методов определения собственных значений и векторов матрицы А основаны на приведении матрицы А с помощью

невырожденных преобразований к такой матрице A* , для которой проблема собственных значений является простой. Например, если А – вещественная матрица с различными вещественными собственными значениями 1 , , n , то

матрица преобразования Т, которая переводит А к диагональному виду полностью решает проблему. Действительно,

a*
	11		0
		*
A*	0	a22		T 1 AT .
			*
			ann

Столбцы матрицы Т образуют полную систему собственных векторов А, а

диагональные элементы матрицы A* являются собственными значениями А. Чтобы определить собственные значения матрицы (при тех же

предположениях относительно i ), не обязательно приводить ее к

диагональному виду. Достаточно привести ее к треугольному виду, т.к. на диагонали будут расположены собственные значения А:

a*		a*	a*
	11	12		1n
		a*	a*			T 1 AT .
A*	0	22		2n
				*
				ann
Действительно, характеристическое уравнение для A*
		det A* E 0
представляется в форме
a*	a*		a*		0
11		22		nn
откуда следует, что собственные			значения			A* –	A* a*	, a*	, , a*	.
							11	22	nn

Осталось показать, что A A* . Это вытекает из равенств det A* E det T 1 AT E det T 1 A E Tdet T 1 det A E det T det A E .

Определение собственных векторов ei* треугольной матрицы A* является простой задачей, т.к. она эквивалентна решению системы однородных

уравнений A*e	a* e ,	i		, с треугольной матрицей и каким-либо
			1, n
i	ii i

дополнительным условием, однозначно выделяющим собственные векторы,

например, e*	1,	i		. Зная собственные векторы матрицы A* , можно
			1, n
ii
получить собственные векторы А с помощью матрицы преобразования Т
				e	Te* ,
				i	i

поскольку из равенства

T 1 ATei* aii* ei*

следует соотношение

A Tei* aii* Tei* .

Замечание. Если вещественная матрица имеет комплексные

собственные значения, она не может быть приведена к треугольной матрице A* с помощью вещественного преобразования. Матрицей, к которой можно привести любую матрицу А с помощью вещественного и даже ортогонального

преобразования, является почти		треугольная			матрица	A* (форма
Хессенберга):
a*		a*		a*
	11	12		1n
a*		a*		a*
A*	21	22		2n	.	(5.1)
	0
			*	*
			an n 1	ann

В задаче определения собственных значений и векторов первым шагом является приведение матрицы А к форме (5.1). Эту процедуру обычно выполняют, чтобы дальнейшие вычисления выполнять с ненулевыми

элементами A* ,, которых при больших n почти вдвое меньше, чем у исходной матрицы А. Для симметричных матриц форма (5.1) принимает трехдиагональный вид:

		a*		a*
			11	12		0
A	*	a21*		a22*	a23*			(5.2)
							.
			0		*	*
					an n 1	ann

5.2. Приведение матрицы к почти треугольному виду

Приведение матрицы А к виду (5.1) будем осуществлять с помощью ортогональных преобразований Т, которые, как известно, сохраняют длину векторов, т.е.

Tx 2 x 2 или Tx,Tx x, x .

При этом матрица ортогонального преобразования Т обладает свойством T 1 T T ; кроме того, произведение ортогональных матриц есть ортогональная

матрица.

В качестве матриц Т будем рассматривать матрицы отражения.

Матрица отражения Т, порожденная вектором

d

d1 , , dn ,

определяется

формулой:

1 0

0

d

2

d

d

d

d

1

1

2

1

n

T E 2dd T

0

1

0

2 d2 d1

d22

d2 dn

(5.3)

0 0

1

d2 dn

2

dn d1

dn

где

d

2 1. Выражения,

полученные

по

формуле (5.3), называют

преобразованием Хаусхолдера.

x

d

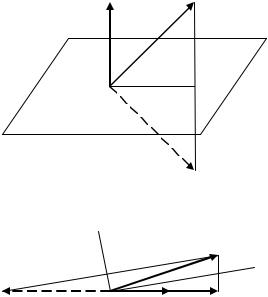
Геометрически матрица T задает

отражение

вектора

x

относительно

плоскости

с

единичным

нормальным

вектором d.

Матрица Т будет симметричной и

ортогональной:

Td d . Если

вектор

x

Tx

ортогонален d, то Tx x .

Построим

элементарное

отражение Т,

который

переводит

заданный

вектор

a a1, a2 , , an

в

a

вектор

коллинеарный

вектору

e1

1,0, ,0 . Таких отражений будет два

(соответствуют знакам ±):

Ta

e1

Ta

Ta

e

a

2

1

Вектор d, порождающий искомое преобразование, задается формулами

d c a1

a

2

, a2 , , an ,

(5.4)

где константа с определяется из условия

d

2

1.

(5.5)

Объединяя (5.3), (5.4) и (5.5), получим искомое отражение Т.

Для однозначного приведения вещественной матрицы А к виду (5.1) обычно используют дополнительное требование, состоящее в том, чтобы значения поддиагонали в (5.1) были одного знака, например,

ai,i 1 0, i 2, n . (5.6)

Это условие выделяет определенный знак в (5.4) и единственное элементарное отражение.

Алгоритм приведения к почти треугольной матрице

следующий.

1 шаг. Определим матрицу n-го порядка:

S		1	0	,
1		0
			T1
								a	21
где T1 – матрица n 1 -го порядка – отражение, переводящее вектор
											в
								an1
вектор, коллинеарный e 1,0, ,0 . Матрица A* S AS 1						S AS имеет вид:
1				1	1	1	1

	*		*
		*	*
		0	*
	A*
		0	*
		0	*

**

**

**

**

* *

*, a21* 0,

* – элементы, которые могут быть ненулевыми. 2 шаг. Определим матрицу n-го порядка:

		1	0	0
S2		0	1	0		,
		0	0	T2

						a*
							32
где T2 – матрица n 2 -го порядка – отражение, переводящее вектор								в
							*
						an2
вектор, коллинеарный e 1,0, ,0 . Матрица	A* S	2	S AS S		2	имеет вид:
1			1	1