1.2. Особенности обработки данных при пассивном эксперименте

В производственных условиях проводится пассивный эксперимент, когда наблюдения входных и выходных параметров производятся случайным образом без изменения режима работы технологического оборудования.

Такое моделирование процесса производства продукции машиностроения включает следующие основные этапы:

– выбор основного эксплуатационного показателя;

– сбор исходной статистической информации, ее систематизацию и оценку;

– отбор существенных факторов, которые необходимо учитывать при построении модели изменения выбранного эксплуатационного показателя;

– построение диаграмм рассеивания, подбор математических форм связи между величиной показателя и влияющими на него факторами;

– расчет параметров и построение математической модели изменения или прогнозирования показателя;

– оценку полученной модели математико-статистическими методами;

– проведение вычислений по модели;

– физическую интерпретацию модели и разработку рекомендаций по ее применению.

Факторы принято разделять на экзогенные, т. е. внешние по отношению к моделируемому объекту, и эндогенные, т. е. внутренние, присущие моделируемому процессу.

Поскольку на эксплуатационные показатели влияет большое количество факторов, задачу моделирования упрощают путем включения в модель существенных факторов.

Моделирование эксплуатационных показателей технологического оборудования пищевых производств основывается на методах и моделях корреляционно-регрессионного анализа. При этом математические модели строят в виде одно- или многофакторных уравнений регрессии, где независимые переменные формируют эксплуатационный показатель. В общем виде такая модель может быть представлена как

S = f (x₁, x₂, x₃, ... x_i, .... x_m, t).

При однофакторном анализе решается задача построения математической модели, описывающей связь эксплуатационного показателя у и одного фактора х.

Вначале для этой цели проводится сбор экспериментальных сведений путем многократного измерения величин у и хi, результаты которых представляются в виде таблицы. По этим результатам строится диаграмма рассеивания в корреляционном поле. Если последовательность точек диаграммы рассеивания группируется в виде некоторой линии, то можно сделать предположение о наличии корреляционной связи.

Затем проводится выбор формы связи путем сравнения внешнего вида диаграммы рассеивания с имеющимися математическими моделями. Линия, которая описывает диаграмму рассеивания, называется линией регрессии, а описывающее ее уравнение называют уравнением регрессии.

Процесс нахождения теоретической линии регрессии называют выравниванием эмпирической линии регрессии. После выбора математической формы связи определяют значения коэффициентов математической модели, пользуясь методом наименьших квадратов.

Понятие о методе наименьших квадратов

Когда вид эмпирической формулы выбран, ставится задача определения ее параметров так, чтобы эта формула наиболее соответствовала имеющимся данным.

Чаще всего при подборе параметров эмпирических формул пользуются методом наименьших квадратов (принципом Лежандра): из формул вида у = f (х) наиболее соответствующей опытным данным считается та, для которой сумма квадратов отклонений от вычисленных эмпирических данных является наименьшей.

Рассмотрим, каким образом этот принцип применяется, например, для определения коэффициентов линейной модели.

Пусть пары значений (x_i; y_i) представлены точками плоскости и лежат примерно на одной прямой, т. е. существует некоторая приближенная линейная зависимость

у = ах + b или ах – у + b = 0.

Если в записанное уравнение подставить координаты эмпирических точек, то в общем случае мы не получим тождества, так как точки только приблизительно лежат на прямой, а получим равенства типа ах_i – у_i + b = _i, где числа _i означают отклонения по ординатам каждой из точек от аппроксимирующей их прямой.

Согласно методу наименьших квадратов, наилучшей функцией вида у = ах + b служит та, для которой сумма квадратов отклонений

S = (₁)² + (₂)² + (₃)² + ... + (_n)²

является наименьшей. Если эта минимальная сумма квадратов окажется малой, то сами погрешности будут малыми по абсолютной величине.

Подставляя в последнее выражение значения _i, получим

S = = f (a, b).

Таким образом, S можно рассматривать как функцию двух переменных а и b, дифференцируемую на всей числовой плоскости. Для искомой прямой (при минимальном отклонении модели от данных) эта сумма должна быть наименьшей. Тогда, в силу необходимого признака экстремума дифференцируемой функции f (a, b), должны соблюдаться условия S/a = 0; S/b= 0. Находя частные производные и приравнивая их нулю, получим

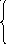
a+ bx_i = x_iу_i,

аx_i + b_n = у_i.

Эту систему называют нормальной системой уравнений для определения параметров а и b функции у = ах + b методом наименьших квадратов.

Для моделей параболического типа решают специальную систему нормальных уравнений, приведенную ниже в табл. 4.

Таблица 4

Системы нормальных уравнений для различных форм связи

Форма связи	Уравнение регрессии	Система нормальных уравнений
Линейная	у = а0 + а1x	а0n + а1хi = yi а0хi + а1хi^2 = xi yi
Парабола	у = а0 + а1x + а2х^2	а0n + а1хi + а2 хi^2 = yi а0хi + а1 хi^2 + а2 хi^3 = xi yi а0 хi^2 + а1 хi^3 + а2 хi^4 =  хi^2 yi

Проще всего провести построение и оценку математической модели, имеющей линейную форму связи. Поэтому часто другие формы связи путем замены переменных приводят к линейной форме, как это показано в табл. 5.

Таблица 5

Замены переменных для линеаризации моделей

Уравнение регрессии	Замена переменных	Линеаризованная форма связи
Гипербола у = а0 +а1(1/х)	z = 1/x	у = а0 + а1z
Показательное у = а0 (а1)^х	у = lg y; a0 = lg a0;	у = a0 + a1x
Степенное у = а0 х^а^1	у = lg y; a0 = lg a0; z = lg x	у = a0 + а1z
Полулогарифмическое у = a0 + а1 lg x	z = lg x	у = a0 + а1z

При наличии больших значений признака его уменьшают путем замены переменной, например, при прогнозировании – вычитанием какой-либо постоянной величины

t = t₀ – 1980.

В дальнейшем вычислительный процесс можно упростить путем отсчета от середины ряда измерений, в соответствии с которыми вводят новую переменную вида

х = х – х = х – 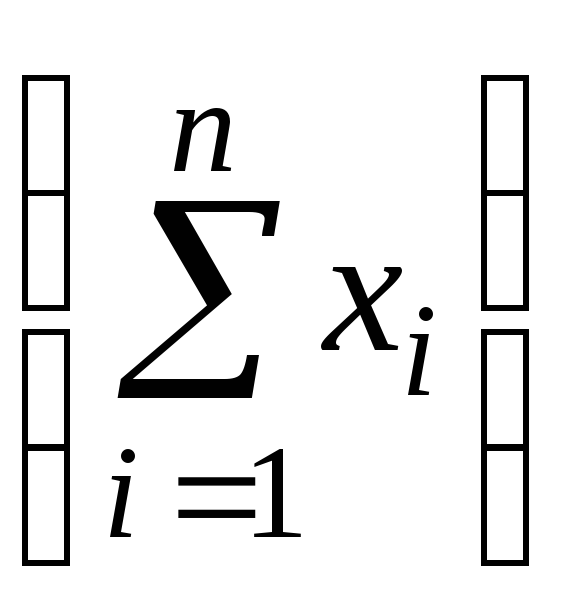/ n,

где х – среднее значение факторного признака; n – число измерений.

Лучше иметь нечетное число измерений. При этом алгебраическая сумма х становится равной 0 и, следовательно, количество членов в системах нормальных уравнений уменьшается, а вычисления сокращаются. Промежуточные же результаты для удобства и наглядности располагают в виде таблицы. Решение систем нормальных уравнений довольно просто осуществляется с помощью ЭВМ.

После определения значений коэффициентов записывают математическую модель, по которой проводят вычисления. По результатам этих вычислений строят график и для сравнения накладывают его на диаграмму рассеивания.

Построенная модель выхода оценивается ее соответствием изучаемому процессу. Значимость модели определяется ее возможностью прогнозировать заданные средние значения выхода независимых переменных.

Для линеаризованных моделей выхода продукта в качестве показателя тесноты связи применяют линейный коэффициент парной корреляции

r = [(xy)* – x*y*]/_x_y,

где x* – среднее значение факторного признака, х* = (х_i)/n; y* – среднее значение результативного признака; (xy)* – среднее значение произведения признаков; n – количество экспериментальных измерений.

Качественную оценку тесноты корреляционной связи между признаками проводят по таблице Чеддока (табл. 6).

Таблица 6

Характеристика тесноты связи между величинами по Чеддоку

Диапазон изменения r	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,99
Характеристика связи	слабая	умеренная	заметная	высокая	весьма высокая

Если r = 0, то связь между признаками отсутствует, если же r = 1, то существует функциональная связь между признаками.

В качестве меры тесноты корреляционной связи между изучаемыми признаками, а также показателя степени близости математической формы связи к фактическим данным, для линейных и нелинейных форм связи применяют корреляционное отношение

 = ,

где  – значение признака, вычисленное по модели; y_i – экспериментальное значение результативного признака.

В качестве меры точности используют среднюю относительную ошибку аппроксимации

* = [(1/n)|(y_i – y*)/ y_i|]  100 %.

При подборе математической формы связи следует ориентироваться на такую, для которой больше корреляционное отношение и меньше средняя относительная ошибка. Если * < (10...20) %, то модель называется достаточно адекватной реальной закономерности.

Поскольку показатели тесноты корреляционной связи исчислены по выборочным данным и являются случайными величинами, то необходимо установить значимость показателей корреляции и коэффициентов модели.

С этой целью определяют ошибку коэффициента корреляции по величине среднего квадратического отклонения

_r = (1 – r²) /.

Затем величина r сопоставляется с _r через отношение t_r = r/_r.

Принято считать, что если t_r = >2, то с вероятностью 0,95 можно говорить о значимости полученного коэффициента корреляции.

Для оценки надежности уравнения регрессии применяют F-кри-терий Фишера:

F_р = /,

где  – дисперсия фактических значений спроса,  = [(y_i – y*)²]/(n – 1);  – остаточная дисперсия,  = [(– y_i)²]/(n – 1– p); р – число коэффициентов в модели.

Показатели f₁ = (n – p – 1) и f₂ = (n – 1) называют числами степеней свободы. Полученное расчетное значение критерия F_р сравнивается с табличным F_т, которое определяется по значениям f₁ и f₂ для заданного уровня значимости  = 0,05.

Если F_р > F_т, то уравнение считается надежным с вероятностью 0,95.

Для оценки значимости коэффициентов линейных моделей сначала находят случайную ошибку для а₀

m₀ = (_ост ) / ,

а затем случайную ошибку для а₁

m₁ = (_ост )/ .

Далее находим фактические значения критерия t_ф для этих коэффициентов

t_ф0 = |а₀|/ m₀; t_ф1 = |а₁|/m₁.

Затем по заданной доверительной вероятности  и соответствующим значениям числа степеней свободы f = (n – p) по таблице Стьюдента [4] определяют критическое значение t_т.

Если при сравнении выполняется неравенство t_ф >  t_т, то коэффициенты признают значимыми, после чего определяют для них доверительные границы

(а₀  m₀ t_т); (а₁  m₁t_т).

При использовании математических моделей расчетные значения могут не совпадать с фактическими, так как линия модели описывает взаимосвязь лишь в среднем и отдельные наблюдения рассеяны вокруг нее. Это происходит по причине воздействия ряда неучтенных факторов, случайных помех и ошибок измерений, поэтому уравнение можно представить в виде

у_х =  у_х,

где у_х – пределы для ; у_х – случайная переменная, характеризующая отклонение.

Полагая, что отклонения фактических значений у от средних распределены по нормальному закону, для любого значения х можно определить доверительное отклонение по формуле

у_х = (t_, f _ост /) ,

где t_, f – значение параметра Стьюдента, определяемое по заданной доверительной вероятности  и числу степеней свободы f.

Зону, в которую попадают все значения случайной величины, можно приближенно вычислить из соображений, приведенных в формулах

y = a₀ + a₁x и L = ; h = t_{, f} _ост/.

y

h

h

y*

h

h

y

L x* L x

Рис. 1. Доверительная область модели

При проведении многофакторного анализа последовательность действий принципиально не меняется. В многофакторную модель включают только те факторы, которые линейно независимы и существенно влияют на изменение результативного признака. Из двух факторов, у которых коэффициент парной корреляции выше 0,8, включают только один. Число включаемых в модель факторов должно быть меньше числа наблюдений.

Пример 2.

Построим модель выхода Y некоторого вида продукции фирмы от объясняющих параметров: Х₁ – время; Х₂ – расходы на сырье; Х₃ – расходы на энергоресурсы; Х₄ – расходы на заработную плату; Х₅ – расходы на оборудование.

Статистические данные по всем переменным приведены в табл. 7.

Таблица 7

Данные пассивного эксперимента о выходе продукции

Выход продукции Y	Изменяемые параметры
	X1	X2	X3	Х4	Х5
126	0	4	15	17	100
137	1	4,8	14,8	17,3	98,4
148	2	3,8	15,2	16,8	101,2
191	3	8,7	15,5	16,2	103,5
274	4	8,2	15,5	16	104,1
370	5	9,7	16	18	107
432	6	14,7	18,1	20,2	107,4
445	7	18,7	13	15,8	108,5
367	8	19,8	15,8	18,2	108,3
367	9	10,6	16,9	16,8	109,2
321	10	8,6	16,3	17	110,1
307	11	6,5	16,1	18,3	110,7
331	12	12,6	15,4	16,4	110,3
345	13	6,5	15,7	16,2	111,8
364	14	5,8	16	17,7	112,3
384	15	5,7	15,1	16,2	112,9

1. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции в пакете прикладных программ Excel.

Для выполнения этой части анализа воспользуемся инструментом Корреляция, для чего необходимо выполнить следующие действия:

а) данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек;

b) выберем команду СервисАнализ данных;

c) в диалоговом окне Анализ данных выберем инструмент Корреляция и нажмем ОК;

d) в диалоговом окне Корреляция в поле «Входной интервал» введем диапазон ячеек, содержащих исходные данные. При выделенных заголовках столбцов установим флажок «Метки в первой строке»;

e) выберем параметры вывода, установим переключатель «Новый рабочий лист»;

f) нажмем ОК, получим результат, изображенный в табл. 8.

Таблица 8

Корреляционная матрица

Наименование параметров	Выход продукции	Время	Расходы на сырье	Расходы на энергоресурсы	Расходы на заработную плату	Расходы на оборудование
Выход продукции	1,000
Время	0,600	1,000
Расходы на сырье	0,646	–0,016	1,000
Расходы на энергоресурсы	0,233	0,118	–0,003	1,000
Расходы на заработную плату	0,226	–0,070	0,204	0,698	1,000
Расходы на оборудование	0,816	0,952	0,273	0,235	0,031	1,000

Анализ матрицы коэффициентов парной корреляции (табл. 8) показывает, что зависимая переменная, т. е. выход продукции, имеет тесную связь с расходами на оборудование (r = 0,816), с расходами на сырье (r = 0,646) и со временем (r = 0,600).

Однако факторы 1 и 5 тесно связаны между собой (r = 0,96), что свидетельствует о наличии мультиколлинеарности. Из этих двух факторов целесообразно оставить в модели Х₅ – расходы на оборудование. Факторы 3 и 4 слабо влияют на выход продукции, так как соответствующие коэффициенты корреляции не достигают 0,3, поэтому их тоже можно не учитывать в модели.

2. Выбор вида модели и оценка ее параметров.

Оценка параметров регрессии осуществляется по методу наименьших квадратов с использованием данных после исключения незначимых параметров. Для проведения анализа с использованием инструмента Регрессия выполняют следующие действия:

а) выбирают команду СервисАнализ данных;

b) в диалоговом окне «Анализ данных» выбирают инструмент Регрессия, после чего нажимают ОК;

c) в диалоговом окне Регрессия в поле «Входной интервал У» вводят адрес диапазона ячеек зависимой переменной, а в другое поле – адрес диапазона для Х₁ и Х₂;

d) устанавливают флажок Метки в первой строке;

e) устанавливают переключатель Новая рабочая книга;

f) в поле «Остатки» ставят необходимые флажки: Остатки и График остатков;

g) нажимают ОК. Полученные результаты приведены в табл. 9.

В табл. 9 как R-квадрат обозначен коэффициент детерминации, который показывает долю вариации результативного признака, находящегося под действием изучаемых факторов. В табл. 10 под df – чис-ло степеней свободы, а F – критерий Фишера. В табл. 11 во втором столбце приведены коэффициенты уравнения регрессии a₀, a₁, a₂, а в четвертом – t-статистики, используемые для проверки значимости коэффициентов. Уравнение регрессии зависимости выхода продукции от расходов на сырье и расходов на оборудование получим, таким образом, в виде Y = –1471,314 + 9,568 Х₁ + 15,754 Х₂.

Таблица 9

Результаты математико-статистической обработки

Наименование показателей	Численные значения
Множественный R	0,926888
R-квадрат	0,859121
Нормированный R-квадрат	0,837447
Стандартная ошибка	41,47298
Наблюдения	16

Таблица 10

Дисперсионный анализ

Наименование показателей	Численные значения
	df	SS	MS	F	Значимость F
Регрессия	2	136358,3	68179,17	39,63887	2,93E-06
Остаток	13	22360,1	1720,008
Итого	15	158718,4

Таблица 11

Параметры уравнения регрессии

Наименование параметров	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	–1471,31	259,766	–5,664
Расходы на сырье	9,568414	2,265936	4,222719
Расходы на оборудование	15,75287	2,466858	6,385804

Распределение остатков свидетельствует о независимости и их нормальном распределении и, следовательно, о правильности выбора типа регрессионной модели.

Вычисленное значение критерия Фишера для доверительной вероятности 0,95 и степеней свободы числителя и знаменателя, соответственно 2 и 13, свидетельствует об адекватности модели, поскольку оно больше табличного (4,81) [4]. Значение рассчитанного t-кри-терия при 5 %-м уровне значимости и степени свободы 13 больше соответствующего табличного (1,77), что также говорит о существенности коэффициентов a₁, a₂.