Ankilov

4. Выберите верные утверждения. Если функция z f (x, y) дифференцируема в точке

M 0 (x0 , y0 ) , то в этой точке она:

а) имеет частные производные; б) непрерывна;

в) имеет предел, равный f (x0 , y0 ) ;

г) имеет частные производные любого порядка; д) имеет полный дифференциал.

5.Какие из следующих функций непрерывны в точке О(0,0)?

а) sin(x2 y 2 ) ; б) ln(1 x2 y 2 ) ;

в)	1			;
	x2 xy
г)	sin xy			;
	x2 y 2
д)	2x 3y		.
	3x 2 y

6. Какие из предыдущих функций дифференцируемы в точке М(1,1)? 7. Если z x y , то частная производная yz равна:

а) yx y 1 ; б) x y ln y ;

в) x y ln x ; г) x y 1 ln y ;

д) yx y 1 ln x .

8.Выберите верные утверждения. Для функции z xy2 точка О(0,0) является:

а) точкой непрерывности; б) стационарной точкой; в) точкой минимума; г) точкой разрыва; д) точкой максимума.

9.Выберите верные утверждения:

а) существование частных производных является достаточным условием дифференцируемости функции;

б) существование частных производных является необходимым условием дифференцируемости функции;

в) непрерывность частных производных является достаточным условием дифференцируемости функции;

г) существование частных производных является необходимым и достаточным условием дифференцируемости функции.

10.Выберите верные утверждения:

а) если	f x/ (x0 , y0 ) 0	и f y/ (x0 , y0 ) 0 , то M 0 (x0 , y0 )	– точка экстремума функции
z f (x, y) ;
б) если M 0 (x0 , y0 ) –		точка максимума дифференцируемой функции z f (x, y) , то
f x/ (x0 , y0 ) 0 и f y/ (x0 , y0 ) 0 ;
в) если	D f xx// (x0 , y0 ) f yy// (x0 , y0 ) f xy// (x0 , y0 ) 2 0 ,		то M 0 (x0 , y0 ) – точка

31

экстремума функции z f (x, y) ;
г) если	M 0 (x0 , y0 ) –	стационарная точка функции z f (x, y)		и D 0 , то	M 0 –
точка максимума;
д) если	M 0 (x0 , y0 )	–	стационарная точка функции z f (x, y) и		D 0 ,
f xx// (x0 , y0 ) 0 , то M 0			– точка минимума.

1.7.2. Задачи Образцы решения задач

Задача 1.1. Найти производные сложной функции

z ln(uv2

2u 2 v) ,

где u

x

, v x sin y .

y 2

Решение. Выполняя действия в соответствии с формулами

z

z

u

z

v

,

z

z

u

z

v

,

x

u

v

x

y

y

y

x

u

v

получим

z

v2 4uv

1

2uv 2u 2

sin y,

x

uv2 2u 2v

y 2

uv2 2u 2v

z

v2 4uv

2x

2uv 2u 2

x cos y.

y

uv

2

2u

2

v

y

3

uv

2

2u

2

v

Вместо u и v подставим их выражения через x и y. После несложных преобразований

	получаем
	z		3	,	z		2 y 2 sin y( y cos y sin y) 8sin y 2 y cos y		.
	x		x		y		y sin y( y 2	sin y 2)

Задача 1.2. Продифференцировать сложную функцию u x3 yz 2 ,

где x sin t,

y

t, z t 2 .

Решение. Так как u является функцией одной независимой переменной t, то задача заключается в вычислении обыкновенной производной dudt . По формуле

du

u dx

u dy

u dz

dt

x dt

y dt

z dt

находим

du

1

3x2 yz 2

cost

x3 z 2

2x3 yz 2t.

dt

2

t

Подставляя вместо x, y, z их выражения через t, будем иметь

du

3sin 2 t

t t 4 cos t sin3 t

t 4

4sin3 t

t

t 3

1 t 3

t sin 2

t(6t cost 9sin t).

dt

2

t

2

32

Задача 2. Доказать, что функция z e

y

удовлетворяет соотношению

x

2 z

2 2 z

x

y

0.

x

x

y 2

Решение. Находим частные производные

z

y

y

z

y

1

2 z

y

1

e x

,

e x

,

e x

,

2

2

2

x

x

y

x

y

x

2 z

2

y

y

y

y

y

y

y

2

x

x

e x

ye x

ye x

e x

.

2

2

x

x

x

x

x

x

x

Подставляя в левую часть соотношения, получаем

y

y 2

2

y

1

e x

y

e x

0,

x2

x

что и требовалось доказать.

Задача 3.1. Найти производную неявной функции y = f(x), заданной уравнением ln(2x 3y) 2x y3 0.

Решение. Производная неявной функции y = f(x), заданной уравнением F(x,y) = 0, вычисляется по формуле

					dy		Fx (x, y)	.
					dx
							Fy (x, y)
	В		данном		случае F(x, y) ln(2x 3y) 2x y3 . Так как				Fx	2	2,
										2x 3y
Fy		3		3y2	, то
	2x 3y

dy		2				3	3y 2			4x 6y 2					2(2x 3y 1)
			2
											2		3				2		3
dx		2x 3y				2x 3y				3 6xy		9 y			3(1	2xy		3y		)

Задача 3.2. Найти частные производные неявной функции z = f(x,y), уравнением

z 2 x x2 y y 2 z 2x y 0.

.

заданной

Решение. Частные производные xz

z Fx (x, y, z) ,

x Fz (x, y, z)

и yz найдем по формулам

z Fy (x, y, z) ,y Fz (x, y, z)

где F(x, y, z) z 2 x x2 y y 2 z 2x y. Имеем						Fx z 2	2xy 2,		Fy x2	2 yz 1,
Fz 2zx y2 , следовательно,
z		2xy z 2 2	,	z		x2 2 yz 1		.
x		2zx y 2		y		2zx y 2

33

Задача 4. Найти экстремумы функции

z 2x4 2 y 4 64x 64 y .

Решение. Сначала найдем стационарные точки данной функции. Для этого составим систему уравнений

z 8x3 64 0x

z 8y3 64 0.

y

Система имеет единственное решение x = 2, y = 2, следовательно, функция имеет одну стационарную точку М(2,2). Далее воспользуемся достаточным признаком экстремума (теорема 1.3.2). Найдем частные производные второго порядка:

	z"xx 24x2 , z"xy 0, z"yy 24 y 2 .
Следовательно,	A z"xx (2,2) 96,	B z"xy (2,2)	0,	C z"yy (2,2) 96,
D AC B2 (96)2 0.
Так как A 96 0, то по теореме		1.3.2 в	точке	М(2,2)	функция
z 2x4 2 y 4 64x 64 y	имеет минимум, равный zmin z(2,2) 192.
Задача 5. Найти условные экстремумы функции z x y 1 при y3				6xy x3	0.
Решение. Составим функцию Лагранжа

L(x, y, ) f (x, y) (x, y),

где z = f(x,y) – исследуемая функция, (x,y) = 0 – уравнение связи, λ – параметр. В данном случае f(x,y) = x + y – 1, (x,y) = y3 – 6xy + x3 , поэтому функция Лагранжа имеет вид

L(x, y, ) x y 1 ( y3 6xy x3 ).

В точках условного экстремума

Lx

1 ( 6y 3x2 ) 0

1 ( 6x 3y 2 ) 0

Ly

y

3

6xy x

3

0.

L

Исключая λ из первого и второго уравнений системы, получим:

1

1

.

3(2 y x2 )

3(2x y 2 )

Отсюда

2 y x2

2x y 2 ,

или 2( y x) (x y)(x y).

Рассмотрим два случая:

1. x – y = 0; подставляя y = x в третье уравнение системы, получаем: 2x3 6x2

0, или

2x2 (x 3) 0, следовательно,

x 0,

x

2

3.

Так как y = x , то y 0,

y

2

3. Если x = 0,

1

1

y = 0, то система несовместна при любом λ. Если x = 3, y = 3, то 19 .

2.–2 = x + y; подставляя y = –2 – x в третье уравнение системы, будем иметь

(2 x)3 6x(2 x) x3 0, (8 12x 6x2 x3 ) 12x 6x2 x3 0,

или 8 0 , что невозможно.

34

Таким образом, система имеет единственное решение x = y = 3,

1

,

значит точка

М(3,3) – точка возможного экстремума.

9

Воспользуемся достаточным

признаком

условного экстремума (теорема 1.3.3). Для

2

,

2

6x,

этого найдем x (x, y) 6 y 3x

y (x, y) 3y

Lxx (x, y, ) 6x

, Lxy (x, y, ) 6 ,

1

, то

2

,

Lyy (x, y, ) 6 y . Если x = y = 3,

9

x 9,

y

9, Lxx 2,

Lxy

3

Lyy 2,

следовательно,

0

x

y

0

9

9

9

2 2 / 3

432 0,

x

Lxx

Lxy

9 2 / 3 2

y

Lxy

Lyy

т. е. функция имеет условный максимум в точке М(3,3), равный zmax z(3,3) 5.

Расчетное задание

Задача 1. Найти производные сложной функции.

1.

u x2 y3 z, где x t, y t 2 ,

z sin t;

du

?

dt

2.

z u 2

v2 , где u x cos y,

v x sin y;

z

?

z

?

x

y

3.

z exy

ln(x y), где x t 3 ,

y 1 t 2 ;

dz

?

dt

4.

z u 2 v uv2 , где u y cos x,

v y sin x;

z

?

z

?

x

y

5.

z x2

xy y 2 , где x cos t,

y sin t;

dz

?

dt

6.

z uv , где u x2 y 2 ,

v x2 y 2 ; z

?

z

?

y

x

7.

z arctg

x 1

, где x t 5

t,

y e1 2t ;

dz

?

dt

y

8.

u

yz

, где x e4t , y ln t,

z cos2 t;

du

?

x

dt

9.

z u 2 v uv3 , где u y

x,

v y cos x;

z

?

z

?

x

y

10.

z u 2 ln v, где u

y

, v x

2 y 4 ; z

?

z

?

x

x

y

Задача 2. Доказать, что функция z = f(x,y) удовлетворяет данному соотношению.

1. z exy , x2 zxx y 2 z yy 0.

	2. z e	cos(2 x y)
			, 4z yy	zxx .

z sin

2

( y 3x),

6.

9z yy

zxx .

7.

z

y

y

,

x

2

y

2

0.

x

zxx

z yy

35

3.z

4.z

5.z

2

2

ln(x

y

2 y 1),

zxx z yy 0.

y

, x

2

2

0.

x

zxx

2xyzxy y

z yy

x

x2

2

z

z

,

y 2

0.

2

y

x

y

y

sin(x

y)

2

z

2

2 z

8.

z

,

x

x

.

x

x

y 2

x

2

2

9.

z ln(x

y

),

zxx z yy 0.

10. z e

x 3 y2

2

,

zx zxy

z y zxx .

Задача 3. Найти производные неявной функции.

1.

z3 3x2 z 2xy ; zx ? z y ?

6. x y y x ; yx ?

2.

exz 2 yz x2 y 2 ; zx ? z y ?

7. ln(x2 y 2 ) arctg

y

;

yx

?

x

1

3.

x2 y y2 z xez 0 ; zx ? z y ?

8. tg(x y)

; yx ?

y

4.

xe y yex 2 ; yx ?

9. z x y arctg z ; zx

?

z y ?

5.

cos2 x cos2

y cos2 z 1 ; zx ? z y ?

10. x2 ln y y 2

ln x 0 ;

yx

?

Задача 4. Найти экстремумы функции.

1. z x4 y 4 32x 8y 2 2.

6. z 3x4 3y 4 12x 12 y.

2.

z 3xy

1

1

.

7. z 5x 6 y ln x 12 ln y.

x

3y

3. z x2 y3 32 ln x 24 ln y.

8. z 3x2 x3 3y2 4 y.

4.

z x3 x2 y xy2 y3 6x 6y.

9. z xy

2

4

.

x

y

5.

z 4xy

2

1

.

10. z x3 y3

3ln x 24 ln y.

x

y

Задача 5. Найти условные экстремумы функции.

1.

z 1

1

,

при x3 y3 16.

x

y

2.

z x2

y 2

xy x y 4,

при x2 y 2

xy 12 (x>0, y>0).

3.

z 3x y,

при x2 y 2 10.

4.

z x y 2 ,

при 2x2 y 4 8 0 (x<0, y>0).

5.

z

x y 4

, при x2 y 2 1.

2

6.

z

y xy x

, при x3 y3

2 0.

xy

7.

z x3

y3 , при x2 y xy2

16.

8.z x 1y , при x4 2 y 2 8.

9.z 4x 3y, при x2 y 2 7.

10.z x3 2xy2 2x2 y y3 1, при x2 y xy2 2 0.

36

ГЛАВА 2. КРАТНЫЕ ИНТЕГРАЛЫ

2.1.Двойной интеграл

2.1.1.Определение и условие существования двойного интеграла

Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функций двух переменных. Пусть D – ограниченная замкнутая область, а z f (x, y) – функция, определенная и ограниченная в этой области.

Разобьем область D произвольно на n частей Di ,	не имеющих общих внутренних
точек, с площадями Si (i = 1,2,…, n). В каждой части	Di выберем произвольную точку
M i (xi , yi ) и составим сумму
n
f (xi , yi ) Si ,	(2.1)
i 1

которая называется интегральной суммой диаметром d(D) области D наибольшее области. Обозначим через

областейDi max d(Di ) .

1 i n

для функции f (x, y) в области D . Назовем расстояние между граничными точками этой наибольший из диаметров частичных

Определение 2.1.1. Если при 0 интегральная сумма (2.1) имеет предел, который

не зависит ни от способа разбиения области D на части,							ни от выбора точек M i , то этот
предел называется двойным интегралом от функции					f (x, y) по области D и обозначается
одним из символов:
f (x, y)dS		или	f (x, y)dxdy .
D				D
В этом случае функция f (x, y) называется интегрируемой в области D .
Таким образом, по определению
		0	n	i	i			i
						) S			.
	f (x, y)dS lim			f (x	, y
D			i 1
Переменные x, y называют переменными интегрирования,							D – областью интегрирования,

f (x, y) – подынтегральной функцией, f (x, y)dS – подынтегральным выражением, dS (или dxdy ) – элементом площади.

При определении двойного интеграла предполагалось, что функция f (x, y) ограничена

в области D . Как и для функций одной переменной, ограниченность функции является необходимым условием ее интегрируемости. Однако оно не является достаточным, так как существуют ограниченные, но не интегрируемые функции. Приведем без доказательства достаточное условие интегрируемости функции двух переменных.

Теорема 2.1.1. Если функция z f (x, y) непрерывна в ограниченной замкнутой области D , то она интегрируема в этой области, т. е. существует двойной интеграл

	0	n	i	i		i
					) S		.
	f (x, y)dS lim		f (x	, y
D		i 1

37

2.1.2. Геометрический смысл двойного интеграла

Пусть в пространстве дано тело T (рис. 2.1), ограниченное снизу областью D , сверху – графиком непрерывной и неотрицательной функции z f (x, y) , которая определена в

области D , с боков – цилиндрической поверхностью, направляющей которой является граница области D , а образующие параллельны оси Оz . Тело такого вида называется

цилиндрическим телом.

z

z f (x, y)

ОT

y

D

x

Рис. 2.1

Аналогично тому, как задача о вычислении площади криволинейной трапеции приводит к установлению геометрического смысла определенного интеграла, так и задача о вычислении объема тела T приводит к геометрическому истолкованию двойного интеграла.

Действительно, интегральная сумма (2.1) представляет собой сумму объемов прямых цилиндров с площадями оснований Si и высотами f (xi , yi ) , которую можно принять за

приближенное значение объема V тела T :

n

Vf (xi , yi ) Si .

i 1

Это приближенное равенство тем точнее, чем мельче разбиение области D на части. Устремляя к нулю, получаем

n

Vlim f (xi , yi ) Si .

0 i 1

Так как функция f (x, y) интегрируема, то предел существует и равен двойному интегралу от этой функции по области D , т. е.

V f (x, y)dS .	(2.2)
D

Отсюда следует геометрический смысл двойного интеграла: двойной интеграл от непрерывной неотрицательной функции равен объему соответствующего цилиндрического тела.

В частности, если f (x, y) 1 всюду в области D , то V S 1, где S – площадь области D , и формула (2.2) принимает вид: dS S .

D

38

2.1.3. Свойства двойного интеграла

Основные свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла. Поэтому ограничимся формулировкой этих свойств, не останавливаясь на их доказательствах.

1. Постоянный множитель можно выносить за знак двойного интеграла:

Af (x, y)dS A f (x, y)dS ,		A = const.
D	D

2. Двойной интеграл от суммы (разности) двух функций равен сумме (разности) двойных интегралов:

f (x, y) g(x, y) dS f (x, y)dS g(x, y)dS .

D D D

3. Если область D является объединением областей D1 и D2 , не имеющих общих внутренних точек, то

f (x, y)dS f (x, y)dS f (x, y)dS .

D

D1

D2

4.Если f (x, y) (x, y) в области D , то

f (x, y)dS (x, y)dS ,

D D

т. е. неравенства можно интегрировать.

В частности, если		f (x, y) 0 , то f (x, y)dS 0 .
		D
5.	Если m f (x, y) M в области D , то
		m S f (x, y)dS M S ,
		D
где S – площадь области D .
6.	Теорема о среднем. Если функция f (x, y) непрерывна в области		D , то в этой
области найдется точка M 0 (x0 , y0 ) такая, что
		f (x, y)dS f (x0 , y0 ) S .	(2.3)
		D
Свойство 6 имеет		следующую геометрическую интерпретацию: если	f (x, y) 0 в

области D , то объем соответствующего цилиндрического тела (левая часть формулы (2.3)) равен объему цилиндра с тем же основанием и высотой f (x0 , y0 ) , равной значению функции

f (x, y) в некоторой точке M 0 (x0 , y0 ) области D . Значение функции f (x0 , y0 ) ,

определяемое формулой (2.3), называется средним значением функции f (x, y) в области D .

7. Абсолютная величина двойного интеграла не превосходит двойного интеграла от абсолютной величины подынтегральной функции:

f (x, y)dS f (x, y)dS .
D	D

39

2.1.4. Вычисление двойного интеграла

Пусть	функция f (x, y)		интегрируема	в области D (рис. 2.2), которая		ограничена
линиями y 1 (x) ,		y 2 (x) ,	x a , x b , причем на отрезке [a, b] функции 1 (x)				и 2 (x)
непрерывны и 1 (x) 2 (x) .
Если	f (x, y)	при любом x a,b		интегрируема по переменной y		на	отрезке
1 (x), 2 (x) , т. е. существует определенный интеграл
			( x)
			S(x) 2 f (x, y)dy,		x a,b ,
			1 ( x)
то справедлива формула
				b	2 ( x)
			f (x, y)dxdy dx		f (x, y)dy .		(2.4)
			D	a	1 ( x)

Интеграл в правой части равенства (2.4) называется повторным интегралом. Сначала вычисляется внутренний интеграл (выполняется интегрирование по y при фиксированном x), а затем – внешний (полученный результат интегрируется по x).

y

y 2 ( x )

		D
О	a			b x
	y = 1(x)
	Рис. 2.2					Рис. 2.3
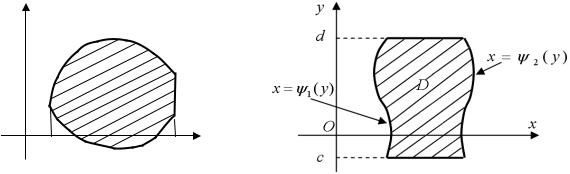
Если область D ограничена линиями					x 1 ( y) , x 2 ( y) ,		y c ,	y d , причем на
отрезке c,d функции 1 ( y)				и 2 ( y) непрерывны и 1 ( y) 2 ( y)			(рис. 2.3), то по аналогии
с формулой (2.4) имеем						2 ( y)
					d
				f (x, y)dxdy dy f (x, y)dx ,				(2.5)
				D	c	1 ( y)

где интегрирование сначала выполняются по x при фиксированном y, а затем полученный результат интегрируется по y.

Если область интегрирования D не удовлетворяет указанным выше условиям (рис. 2.4), ее необходимо разбить на части D1 , D2 ,..., Dn , которые допускают применение

формул (2.4), (2.5), при этом

f (x, y)dxdy f (x, y)dxdy f (x, y)dxdy ... f (x, y)dxdy .

D D1 D2 Dn

40