Ankilov

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Ульяновский государственный технический университет

А. В. Анкилов, П. А. Вельмисов, Ю. А. Решетников

Высшая математика

(Часть 2)

Учебное пособие

Ульяновск

2009

УДК 51 (075) ББК 22.311 я7 А67

Рецензенты: кафедра прикладной математики УлГУ (зав. кафедрой д-р физ.-мат. наук, профессор А. А. Бутов); д-р физ.-мат. наук, профессор УлГУ А. С. Андреев.

Под общей редакцией д-ра физ.-мат. наук, профессора П. А. Вельмисова

Утверждено редакционно-издательским советом университета в качестве учебного пособия.

	Анкилов, А. В.
A 67	Высшая математика (Часть 2) : учебное пособие / А. В. Анкилов,
	П. А. Вельмисов, Ю. А. Решетников; под общей редакцией

П. А. Вельмисова. – Ульяновск: УлГТУ, 2009. – 272 с.

ISBN 978-5-9795-0514-5

Пособие предназначено для студентов всех специальностей, изучающих дисциплину «Математика».

Работа выполнена на кафедре «Высшая математика» УлГТУ. Печатается в авторской редакции.

	УДК 51 (075)
	ББК 22.311 я7
	Анкилов А. В., Вельмисов П. А.,
	Решетников Ю. А., 2009
ISBN 978-5-9795-0514-5	Оформление. УлГТУ, 2009

ОГЛАВЛЕНИЕ
Введение......................................................................................................................................	7
Глава 1. Дифференциальное исчисление функций нескольких переменных.......	8
1.1. Определение, предел и непрерывность функций нескольких переменных.................	8
1.1.1. Определение функции нескольких переменных.......................................................	8
1.1.2. Предел функции нескольких переменных.................................................................	9
1.1.3. Непрерывность функции нескольких переменных................................................	10
1.2. Частные производные и дифференцируемость функций нескольких переменных..	12
1.2.1. Частные производные................................................................................................	12
1.2.2. Дифференцируемость функции, полный дифференциал.......................................	13
1.2.3. Производные сложных функций..............................................................................	15
1.2.4. Производные неявных функций...............................................................................	17
1.2.5. Частные производные высших порядков................................................................	18
1.3. Экстремумы функций нескольких переменных ...........................................................	19
1.3.1. Необходимые условия экстремума..........................................................................	19
1.3.2. Достаточные условия экстремума............................................................................	20
1.3.3. Условный экстремум.................................................................................................	21
1.3.4. Метод наименьших квадратов..................................................................................	24
1.4. Основные термины..........................................................................................................	26
1.5. Вопросы для самоконтроля.............................................................................................	27
1.6. Задачи для самостоятельного решения..........................................................................	27
1.7. Итоговый контроль..........................................................................................................	30
1.7.1. Тест..............................................................................................................................	30
1.7.2. Задачи..........................................................................................................................	32
Глава 2. Кратные интегралы...............................................................................................	37
2.1. Двойной интеграл............................................................................................................	37
2.1.1. Определение и условие существования двойного интеграла................................	37
2.1.2. Геометрический смысл двойного интеграла...........................................................	38
2.1.3. Свойства двойного интеграла...................................................................................	39
2.1.4. Вычисление двойного интеграла..............................................................................	40
2.1.5. Замена переменных в двойном интеграле...............................................................	43
2.1.6. Приложения двойного интеграла.............................................................................	46
2.2. Тройной интеграл.............................................................................................................	50
2.2.1. Определение и вычисление тройного интеграла....................................................	50
2.2.2. Замена переменных в тройном интеграле...............................................................	52
2.2.3. Приложения тройного интеграла.............................................................................	55
2.3. Основные термины..........................................................................................................	56
2.4. Вопросы для самоконтроля.............................................................................................	56
2.5. Задачи для самостоятельного решения..........................................................................	57
2.6. Итоговый контроль..........................................................................................................	59
2.6.1. Тест..............................................................................................................................	59
2.6.2. Задачи..........................................................................................................................	62
Глава 3. Криволинейные и поверхностные интегралы..............................................	67
3.1. Криволинейные интегралы.............................................................................................	67
3.1.1. Задача, приводящая к понятию криволинейного интеграла первого рода.........	67
3.1.2. Определение криволинейного интеграла первого рода, его физический
и геометрический смысл..................................................................................................	68

3

3.1.3. Вычисление криволинейного интеграла первого рода..........................................	69
3.1.4. Криволинейный интеграл второго рода и его физический смысл........................	70
3.1.5. Вычисление криволинейного интеграла второго рода ..........................................	72
3.1.6. Формула Грина...........................................................................................................	73
3.1.7. Условие независимости криволинейного интеграла от пути интегрирования....	76
3.2. Поверхностные интегралы..............................................................................................	78
3.2.1. Поверхностный интеграл первого рода...................................................................	78
3.2.2. Поверхностный интеграл второго рода...................................................................	81
3.2.3. Формула Остроградского-Гаусса.............................................................................	84
3.2.4. Формула Стокса.........................................................................................................	86
3.3. Основные термины..........................................................................................................	87
3.4. Вопросы для самоконтроля.............................................................................................	87
3.5. Задачи для самостоятельного решения..........................................................................	88
3.6. Итоговый контроль..........................................................................................................	89
3.6.1. Тест..............................................................................................................................	90
3.6.2. Задачи..........................................................................................................................	91
Глава 4. Элементы теории поля..........................................................................................	97
4.1. Скалярное поле. Производная по направлению и градиент скалярного поля...........	97
4.2. Векторное поле.................................................................................................................	99
4.2.1. Понятие векторного поля. Векторные линии..........................................................	99
4.2.2. Поток векторного поля............................................................................................	101
4.2.3. Дивергенция векторного поля................................................................................	102
4.2.4. Циркуляция векторного поля..................................................................................	104
4.2.5. Ротор векторного поля.............................................................................................	106
4.2.6. Простейшие векторные поля..................................................................................	107
4.2.7. Оператор Гамильтона..............................................................................................	109
4.3. Основные термины........................................................................................................	110
4.4. Вопросы для самоконтроля...........................................................................................	110
4.5. Задачи для самостоятельного решения........................................................................	111
4.6. Итоговый контроль........................................................................................................	112
4.6.1. Тест............................................................................................................................	113
4.6.2. Задачи........................................................................................................................	115
Глава 5. Ряды...........................................................................................................................	120
5.1. Числовые ряды...............................................................................................................	120
5.1.1. Определение ряда и его сходимость......................................................................	120
5.1.2. Свойства сходящихся рядов ...................................................................................	122
5.1.3. Знакоположительные ряды.....................................................................................	123
5.1.4. Знакопеременные ряды ...........................................................................................	126
5.2. Степенные ряды.............................................................................................................	129
5.2.1. Степенной ряд. Область сходимости.....................................................................	129
5.2.2. Разложение функций в степенные ряды................................................................	132
5.3. Ряды Фурье.....................................................................................................................	136
5.3.1. Тригонометрический ряд. Ортогональность основной
тригонометрической системы........................................................................................	136
5.3.2. Ряд Фурье. Сходимость ряда Фурье.......................................................................	137
5.3.3. Ряд Фурье для четных и нечетных функций.........................................................	141
5.3.4. Ряд Фурье для 2l-периодической функции ...........................................................	143
5.3.5. Ряд Фурье для непериодической функции............................................................	144
5.4. Основные термины........................................................................................................	146

4

5.5. Вопросы для самоконтроля...........................................................................................	147
5.6. Задачи для самостоятельного решения........................................................................	148
5.7. Итоговый контроль........................................................................................................	149
5.7.1. Тест............................................................................................................................	150
5.7.2. Задачи........................................................................................................................	151
Глава 6. Обыкновенные дифференциальные уравнения.........................................	156
6.1. Дифференциальные уравнения первого порядка........................................................	156
6.1.1. Основные понятия ...................................................................................................	156
6.1.2. Уравнения с разделяющимися переменными.......................................................	157
6.1.3. Однородные уравнения первого порядка..............................................................	158
6.1.4. Линейные уравнения первого порядка. Уравнения Бернулли............................	160
6.1.5. Уравнения в полных дифференциалах..................................................................	162
6.2. Дифференциальные уравнения высших порядков.....................................................	163
6.2.1. Дифференциальные уравнения n-го порядка – основные понятия.....................	163
6.2.2. Уравнения, допускающие понижения порядка.....................................................	164
6.3. Линейные дифференциальные уравнения...................................................................	166
6.3.1. Основные понятия ...................................................................................................	166
6.3.2. Линейные дифференциальные уравнения с постоянными коэффициентами....	168
6.3.3. Линейные уравнения второго порядка с переменными коэффициентами.
Метод вариации произвольных постоянных................................................................	170
6.3.4. Понятие о краевой задаче........................................................................................	172
6.4. Системы дифференциальных уравнений.....................................................................	172
6.4.1. Основные понятия ...................................................................................................	172
6.4.2. Метод исключения неизвестных............................................................................	174
6.4.3. Метод Эйлера...........................................................................................................	174
6.5. Основные термины........................................................................................................	176
6.6. Вопросы для самоконтроля...........................................................................................	176
6.7. Задачи для самостоятельного решения........................................................................	177
6.8. Итоговый контроль........................................................................................................	179
6.8.1. Тест............................................................................................................................	179
6.8.2. Задачи........................................................................................................................	182
Глава 7. Численные методы и их реализация в системе MathCAD......................	189
7.1. Решение систем линейных уравнений методом Гаусса.............................................	190
7.1.1. Постановка задачи ...................................................................................................	190
7.1.2. Задание на лабораторную работу...........................................................................	192
7.1.3. Порядок выполнения работы в компьютерном классе........................................	193
7.1.4. Программа в системе MathCAD и тестирующий пример....................................	194
7.1.5. Расчетная часть лабораторной работы для тестирующего примера...................	200
7.1.6. Основные термины..................................................................................................	202
7.1.7. Вопросы для самоконтроля.....................................................................................	202
7.2. Решение нелинейных уравнений..................................................................................	204
7.2.1. Постановка задачи ...................................................................................................	204
7.2.2. Отделение корней уравнения. Графический метод..............................................	204
7.2.3. Метод половинного деления...................................................................................	205
7.2.4. Метод Ньютона........................................................................................................	205
7.2.5. Метод хорд ...............................................................................................................	206
7.2.6. Комбинированный метод........................................................................................	207
7.2.7. Задание на лабораторную работу...........................................................................	208
7.2.8. Порядок выполнения работы в компьютерном классе........................................	209

5

7.2.9. Программа в системе MathCAD и тестирующий пример....................................	210
7.2.10. Расчетная часть лабораторной работы для тестирующего примера.................	216
7.2.11. Основные термины................................................................................................	219
7.2.12. Вопросы для самоконтроля...................................................................................	220
7.3. Вычисление определенных интегралов.......................................................................	221
7.3.1. Постановка задачи ...................................................................................................	221
7.3.2. Методы прямоугольников и трапеций...................................................................	222
7.3.3. Метод Симпсона......................................................................................................	223
7.3.4. Оценка погрешностей методов...............................................................................	224
7.3.5. Задание на лабораторную работу...........................................................................	226
7.3.6. Порядок выполнения работы в компьютерном классе........................................	227
7.3.7. Программа в системе MathCAD и тестирующий пример....................................	228
7.3.8. Расчетная часть лабораторной работы для тестирующего примера...................	233
7.3.9. Основные термины..................................................................................................	236
7.3.10. Вопросы для самоконтроля...................................................................................	236
7.4. Дифференциальные уравнения первого порядка........................................................	237
7.4.1. Постановка задачи ...................................................................................................	237
7.4.2. Метод Эйлера...........................................................................................................	238
7.4.3. Метод Рунге-Кутта ..................................................................................................	239
7.4.4. Выбор шага интегрирования...................................................................................	239
7.4.5. Задание на лабораторную работу...........................................................................	240
7.4.6. Порядок выполнения работы в компьютерном классе........................................	241
7.4.7. Программа в системе MathCAD и тестирующий пример....................................	242
7.4.8. Расчетная часть лабораторной работы для тестирующего примера...................	246
7.4.9. Основные термины..................................................................................................	249
7.4.10. Вопросы для самоконтроля...................................................................................	249
7.5. Аппроксимация функции на основании экспериментальных данных по методу
наименьших квадратов.......................................................................................................	250
7.5.1. Постановка задачи ...................................................................................................	250
7.5.2. Выбор типа кривой..................................................................................................	250
7.5.3. Метод наименьших квадратов................................................................................	251
7.5.4. Подбор параметров квадратичной функции методом наименьших квадратов.	252
7.5.5. Задание на лабораторную работу...........................................................................	253
7.5.6. Порядок выполнения работы в компьютерном классе........................................	254
7.5.7. Программа в системе MathCAD и тестирующий пример....................................	255
7.5.8. Расчетная часть лабораторной работы для тестирующего примера...................	261
7.5.9. Основные термины..................................................................................................	264
7.5.10. Вопросы для самоконтроля...................................................................................	264
7.6. Прикладной математический пакет «Mathcad» ..........................................................	265
7.6.1. О программе.............................................................................................................	265
7.6.2. Основные понятия и функции................................................................................	265
7.6.3. Операторы математического анализа....................................................................	267
7.6.4. Функции и операторы матриц................................................................................	268
7.6.5. Создание декартовых графиков на плоскости......................................................	269
7.6.6. Программные блоки.................................................................................................	270
Заключение...............................................................................................................................	272
Библиографический список................................................................................................	272

6

ВВЕДЕНИЕ

Данная книга является второй частью учебного пособия по дисциплине «Математика»

инаписана в соответствии с программой дисциплины для инженерно-технических специальностей высших учебных заведений. Предназначено для студентов всех специальностей, изучающих дисциплину «Математика». Пособие содержит следующие разделы дисциплины: дифференциальное исчисление функций нескольких переменных; кратные интегралы; криволинейные и поверхностные интегралы; элементы теории поля; ряды; обыкновенные дифференциальные уравнения; численные методы.

Вкниге каждый из перечисленных выше разделов представлен отдельной главой. Главы разбиты на подразделы, каждый из которых содержит необходимые теоретические сведения и их применение к решению типовых примеров и задач.

Вконце каждой из глав 1 – 6 приведены список основных терминов, вопросы для самоконтроля и задачи для самостоятельного решения. Итоговый контроль по каждому разделу включает в себя тест и расчетное задание из 5–6 задач. Каждая задача предлагается в 10 вариантах, приводятся также образцы решения аналогичных задач.

Вглаве 7 для ознакомления студентов с основными численными методами, разработан цикл из 5 лабораторных работ. Каждая лабораторная работа описывается в отдельном подразделе и предлагается в 30 вариантах. Приводятся образцы решения аналогичных работ. В конце каждого подраздела приведены контрольные вопросы и список основных терминов.

Врезультате изучения пособия студент должен знать основные математические понятия, методы и факты, обеспечивающие широкий спектр их применения, разумную точность формулировок математических свойств изучаемых объектов, уметь логически мыслить, оперировать с абстрактными объектами и использовать полученные знания для решения стандартных задач.

Вразделе «Дифференциальное исчисление функций нескольких переменных» проводится ознакомление с основными понятиями и их применением к исследованию функций.

Цель изучения кратных интегралов – ознакомление с понятиями двойного и тройного интеграла, с правилами их вычисления и некоторыми физическими и геометрическими приложениями этих интегралов.

Вследующем разделе проводится ознакомление с понятиями криволинейных и поверхностных интегралов, с правилами их вычисления и основными приложениями этих интегралов.

Вразделе «Элементы теории поля» проводится ознакомление с понятиями скалярного

ивекторного полей и основными характеристиками этих полей.

Решение многих задач математики и ее приложений значительно упрощается, если рассматриваемые функции представлять как ряды, членами которых являются функции простейшего вида. Целью изучения раздела «Ряды» является ознакомление с основными понятиями теории рядов и методами представления функций рядами Тейлора и Фурье.

Решение многих физических задач сводится к решению дифференциальных уравнений. Целью изучения темы «Обыкновенные дифференциальные уравнения» является ознакомление с понятием обыкновенного дифференциального уравнения и методами решения простейших дифференциальных уравнений и их систем.

Математическое образование инженера в настоящее время не может ограничиваться традиционными разделами классического анализа. От инженера требуется знание многих разделов современной математики, так как решение почти каждой инженерной задачи должно быть доведено до численного результата. В то же время решение многих задач приводит к исследованию сложных математических моделей. В тех случаях, когда не удается получить точных аналитических решений, используются численные методы, изучаемые в одноименном разделе.

7

ГЛАВА 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

1.1. Определение, предел и непрерывность функций нескольких переменных

1.1.1. Определение функции нескольких переменных

При рассмотрении многих вопросов естествознания приходится иметь дело с такими зависимостями между переменными величинами, в которых числовые значения одной из них полностью определяются значениями нескольких других. Так, например, температура тела в данный момент времени t может изменяться от точки к точке. Каждая точка тела определяется тремя координатами x , y и z , поэтому температура зависит (является

функцией) от трех переменных x , y , z , а если еще учитывать зависимость температуры от времени t , то значения ее будут уже определяться значениями четырех переменных x , y , z

и t . Примеров таких зависимостей можно привести сколько угодно. В данной главе изучаются такого рода зависимости. С этой целью вводится понятие функции нескольких переменных и развивается аппарат для исследования таких функций.

Между функциями одной и функциями нескольких переменных много общего, но имеются и существенные различия. В то же время переход от двух переменных к большему их числу, как правило, не представляет затруднений. В связи с этим в дальнейшем подробно будет рассматриваться только случай функций двух переменных.

Определение 1.1.1. Пусть D – множество упорядоченных пар чисел (x, y) . Если каждой паре (x, y) D поставлено в соответствие число z , то говорят, что на множестве D задана функция z f (x, y) от двух переменных x и y .

Переменные x и y называют независимыми переменными (аргументами), переменную

z – зависимой переменной, множество D – областью определения функции.

Так как каждой паре чисел (x, y) соответствует на плоскости точка M с координатами (x, y) , то функцию двух переменных можно рассматривать как функцию точки M и вместо

z f (x, y)		писать		z f (M ) .	Областью определения функции в этом случае является
некоторое множество M точек плоскости.
	Как	известно,		графиком	функции одной		переменной	y f (x) является			кривая,
определенная уравнением y f (x) .						Функцию двух переменных			z f (x, y)	также можно
				z		представить графиком.			Это будет	поверхность,
						которая определяется уравнением z f (x, y) , т. е.
						сама формула, задающая функцию, и есть уравнение
						этой поверхности.
	z x2 y2					В аналитической геометрии рассматриваются
						различные	поверхности и их уравнения. Так,
				O	y	например,	уравнение	z 2x 5y 10 0			является
						уравнением плоскости. Данная плоскость есть
	x					график	функции	z 2x 5y 10 .		Графиком
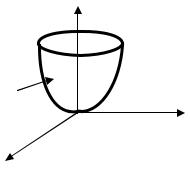
			Рис. 1.1			функции z x2 y2 является параболоид вращения

(рис. 1.1).

8

Построение графиков функций двух переменных во многих случаях представляет значительные трудности, поэтому основным способом задания функций двух переменных является аналитический. Областью определения функции в этом случае является множество точек плоскости, для которых формула, определяющая функцию, имеет смысл.

Пример 1.1.1. z 2x2 y2 x . Область определения этой функции – вся плоскость Oxy , так как x и y могут принимать любые значения.

	Пример 1.1.2. z		1 x2 y2		. Областью определения является множество всех точек,
для	которых	выражение		1 x2	y2 определено, т. е. множество точек,	таких, что
1 x2	y2 0 ,	или x2 y2		1. Множество всех таких точек образует круг		единичного

радиуса с центром в начале координат.

Если вместо множества точек плоскости взять множество M точек пространства, то аналогично можно дать определение функции трех переменных u f (M ) или u f (x, y, z) . Областью определения функции трех переменных является все пространство или его часть.

Так, например, функция		u x y2 z3 определена во всем		пространстве, а функция
u ln xyz	– на множестве точек пространства, координаты			которых удовлетворяют
неравенству	xyz 0 . Определение функции n		(n 3) переменных аналогично данному
выше определению 1.1.1,		при этом используется символическая запись u f (x1 , x2 ,..., xn )

или u f (M ) , где M – точка n-мерного пространства Rn. Заметим, что при n 3 область определения функции уже не имеет наглядного геометрического истолкования.

1.1.2.Предел функции нескольких переменных

Вдальнейшем функцию двух переменных будем рассматривать, как правило, не на произвольном множестве точек плоскости, а на множестве, которое называется областью. Областью будем называть часть плоскости, ограниченную одной или несколькими непрерывными кривыми. Совокупность этих кривых называется границей области. Введем

понятие -окрестности данной точки M 0 (x0 , y0 ) .
Определение 1.1.2. Множество всех точек				M (x, y) , координаты которых
удовлетворяют неравенству		x x0 2 y y0 2	<δ,	или, короче, (M , M 0 ) ,
называется -окрестностью точки M 0 (x0 , y0 ) .
Другими словами, -окрестность точки M 0 –			это все точки, лежащие внутри круга
радиуса с центром в точке M 0		(x0 , y0 ) .
Всюду далее,	если говорится, что функция f (x, y)			обладает каким-либо свойством в
окрестности точки	M 0 (x0 , y0 ) , то под этим подразумевается, что найдется круг с центром

(x0 , y0 ) , во всех точках которого данная функция обладает указанным свойством. Теперь

дадим определение предела функции двух переменных. Оно аналогично определению предела функции одной переменной.

Пусть функция z f (x, y) определена в некоторой области D плоскости Оxy и пусть M 0 (x0 , y0 ) – точка, лежащая в области D или на ее границе.

Определение 1.1.3. Число A называется пределом функции z f (x, y) при стремлении

точки	M (x, y) к точке M 0			(x0 , y0 ) ,			если для любого числа 0	существует число 0
такое,	что для всех точек			M (x, y) ,			удовлетворяющих условию	0 (M , M 0 ) , имеет
место неравенство			f (x, y) A			.

9

Обозначение: lim f (x, y) A или lim					f (M ) A .
x x0			M M0
y y0
Заметим, что задача нахождения предела функции двух переменных является более
сложной, чем для функции одной переменной.
Пример 1.1.3. Найти lim		xy		.
		xy 9
y 0 3
x 0
Положим xy = t, тогда t 0 при x 0					и y 0 .

lim

xy

= lim

t

=

lim

t(3

t 9) = lim (3

t 9) = –6.

x 0

3

xy 9

t 0

3

t

9

t 0

9 (t 9)

t 0

y 0

Не следует думать, что предел функции двух переменных можно найти, вычисляя

последовательно пределы по каждой из переменных.

xy

, если x

2

y

2

0

2

y

2

Пример 1.1.4. Пусть f (x, y) x

2

y

2

0 .

0 , если x

Тогда

f (0, y) f (x,0) 0 ,

а

f (x, x)

1

при x 0.

Таким образом, функция не имеет

предела при (x, y) (0,0) , хотя

2

lim(lim f (x, y)) lim 0 0 ,

lim(lim f (x, y)) lim 0 0 .

y 0 x 0

y 0

y 0

x 0

y 0

1.1.3. Непрерывность функции нескольких переменных

Понятие непрерывности функции вводится на основе понятия предела. Пусть функция z f (x, y) определена в области D и точка M 0 (x0 , y0 ) D .

Определение 1.1.4. Функция z f (x, y) называется непрерывной в точке M 0 (x0 , y0 ) , если предел функции в этой точке существует и равен значению функции в этой точке, т. е.

lim f (x, y) f (x0 , y0 ) .						(1.1)
x x0
y y0
Функция называется непрерывной в некоторой области, если она непрерывна в каждой
точке этой области.
Если в некоторой точке M 0 условие (1.1) не выполняется,						то точка M 0 называется
точкой разрыва функции z f (x, y) .
Пример 1.1.5. Функция f (x, y)		2	y	2	, всюду, кроме x 1, y	2
	x
	0 , при x 1, y 2
в точке M 0 (1,2) разрывна, так как lim	f (x, y) 5 , а f (1,2) 0 .
x 1
y 2
Сформулируем определение непрерывности в терминах приращений. Полным
приращением функции z f (x, y) в точке M 0					(x0 , y0 ) называется величина

z f (x0 x, y0 y) f (x0 , y0 ) ,

10