Ankilov

		z
y						z=f(x,y)
	D1				S(x)	y=f (x)
	D
		D				y = φ22(x)
	2	3
О				y		D
		x
					y=fφ1(x)x)		x
		0	a	x	1
					b
	Рис. 2.4				Рис. 2.5
Установим справедливость формулы (2.4), предполагая дополнительно, что							f (x, y) 0
в области	D . В этом случае двойной интеграл в левой части равенства (2.4) есть объем V
цилиндрического тела (рис. 2.5), т. е.

V f (x, y)dxdy .	(2.6)
D
Проведем плоскость x = const ( a x b ), рассекающую рассматриваемое тело.
В сечении получим криволинейную трапецию, ограниченную снизу	отрезком

1 (x) y 2 (x) , а сверху – кривой z f (x, y) , x = const. Ее площадь выразится интегралом

2 ( x)
S(x)	f (x, y)dy .	(2.7)
1 ( x)
Зная площади поперечных сечений, объем тела можно найти по формуле
V b S(x)dx .		(2.8)
	a
Подставляя в (2.8) выражение (2.7), получаем
b	2 y
V dx	f x, y dy.	(2.9)
a	1 y

В формулах (2.6) и (2.9) левые части равны, следовательно, равны и правые, т. е. формула (2.4) справедлива. Аналогично доказывается формула (2.5).

Таким образом, чтобы найти двойной интеграл, надо представить его в виде повторного, применяя формулы (2.4), (2.5); затем последовательно проинтегрировать по каждой переменной. Выбор формулы приведения к повторному интегралу зависит как от вида области D , так и от вида подынтегральной функции.

Пример 2.1.1. Вычислить интеграл xdxdy , где область D ограничена линиями

D

xy = 4, x+y = 5.

41

Решение. Изобразим на плоскости область D (рис. 2.6) и воспользуемся формулой

	(2.4). В данном случае 1 (x)															4	, 2 (x) 5 x , 1 x 4 . Согласно формуле (2.4) имеем
																x																					4
		4		5 x				4					5 x					4								5x2		x3										64
	xdxdy dx						xdy (xy						4		)dx (x(5 x)									4)dx (								4x)					= (40	3	16)
																										2		3
	D	1			4			1					x					1																			1
					x											– ( 5		1 4) 8						11 4,5 .
															2			3	3					6
	Данный	интеграл						можно							вычислить				и по формуле (2.5).													Замечая, что область D
определяется		неравенствами											4		x 5 y ,					1 y 4 , т. е.							1 ( y)							4			, 2 ( y) 5 y ,			c 1 ,
														y																						y
d 4 , и применяя формулу (2.5), получаем
	4	5 y					4	x	2		5 y						4	(5 y)	2		8					(5 y)		3		4		8				4	1 32
xdxdy dy				xdx (									)dy												dy													2 8 4,5 .
																					2
D	1	4					1	2			4						1	2				y					6			1			y			1	6 3
											y
			y
	Пример 2.1.2. Вычислить интеграл																		e			y
																						x	dxdy , где область										D				ограничена прямыми
y x , y 0 , x 1.																			D
	Решение.			Область					D – треугольник (рис. 2.7), ограниченный снизу прямой																															y 0 ,
сверху – прямой y x , 0 x 1 .

		y
	5
	4			y = 5 – x
	4
y				D
	x
	1
		О 1	4 5		x

Рис. 2.6

Применяя формулу (2.4), будем иметь:

y
1
	y = x
	D
О	x
	1
	Рис. 2.7

e y x dxdy 1		dx x	e y x dy 1	xe y x		0x dx 1	xe x dx e 1	x2		1	e 1 .
D	0	0	0		0		2			0	2

В данном случае вид подынтегральной функции не позволяет воспользоваться формулой (2.5). Действительно,

ey x dxdy 1 dy 1 e y x dx ,

D

0

y

но eyx dx не выражается в элементарных функциях.

42

2.1.5. Замена переменных в двойном интеграле

Метод замены переменной является одним из основных методов вычисления определенного интеграла. В двойном интеграле две переменных, поэтому правило их замены

более сложное.
Пусть функция f x, y непрерывна в ограниченной замкнутой области	D . Тогда для
функции f x, y существует двойной интеграл
f x, y dxdy .	(2.10)
D
Введем новые переменные u, v c помощью формул:
x x u,v , y y u,v .	(2.11)

Предположим, что из (2.11) единственным образом определяются u, v :

	u u x, y , v v x, y .	(2.12)
Согласно формулам (2.12)	каждой точке М (x, y) из области	D ставится в соответствие
некоторая точка М* u, v на координатной плоскости с прямоугольными координатами u иv .
Если обозначить через D*	множество всех точек М* u, v , то каждой точке М* u, v из D*

будет соответствовать точка М (x, y) из D , координаты которой определяются формулами (2.11). Таким образом, формулы (2.11) устанавливают взаимно однозначное соответствие

между точками областей D и D* . Говорят также, что преобразование координат (2.11) является взаимно однозначным.

При сделанных предположениях можно доказать, что если функции (2.11) имеют в области D* непрерывные частные производные первого порядка, то определитель

D x, y			x	x
			u	v	(2.13)
D u, v			y	y
			u	v

отличен в D* от нуля, и для интеграла (2.10) справедлива формула

	f x, y dxdy f x u, v , y u, v			D x, y			dudv .	(2.14)
				D u, v
	D	D*

Определитель (2.13) называется функциональным определителем Якоби или якобианом

функций x x u, v , y y u, v по переменным u и v .

Точнее, имеет место Теорема 2.1.2. Если преобразование (2.11) переводит ограниченную замкнутую

область D в ограниченную замкнутую область D* и является взаимно однозначным и если функции (2.11) имеют в области D* непрерывные частные производные первого порядка, а функция f (x, y) непрерывна в области D, то справедлива формула замены переменных

(2.14).

Доказательство теоремы достаточно сложное и здесь не приводится.

Как и в определенном интеграле, замена переменных в двойном интеграле производится с целью приведения его к виду, более удобному для вычисления.

Пример 2.1.3. Вычислить интеграл 2x y dx dy,

где D параллелограмм,

D

ограниченный прямыми x + y = 1, x + y = 2, 2x – y = 1, 2x – y = 3 (рис. 2.8, а).

43

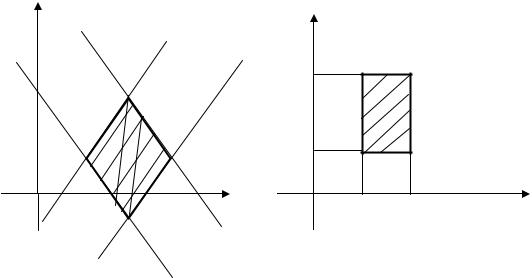
Непосредственное вычисление данного интеграла достаточно громоздкое, так как для сведения его к повторному (сначала по y, а затем по x) необходимо область D разбить на три части (штриховые линии на рис. 2.8, а) и затем вычислить соответственно три интеграла. Однако простая замена переменных

		x y u, 2x y v		(2.15)
позволяет значительно упростить решение. Прямые x y 1,			x y	2 в системе координат
Оxy переходят в прямые u = 1, u =		2 в системе координат Ou v		(рис. 2.8, б), а прямые
2x y 1, 2x y 3 в	прямые v 1 и v 3. Параллелограмм			D взаимно однозначно
преобразуется в прямоугольник D*, который является более простой областью
интегрирования.
y		v
x + y = 2
	2x – y = 1	2x – y = 3
x + y = 1
		3
			D*
	D	1

x	O		u
O		1	2

а

б

Рис. 2.8

Найдем якобиан. Для этого из (2.15) выразим x и y через u и v:

						x	u v						, y					2u v .
								3												3
Следовательно,
				D(x, y)						1			1						1				2			1 .
										3			3
				D(u,v)						2			1						9 9							3
										3			3
По формуле (2.14) получаем
			1		1	2		3						1		2				2		3				1 9			1		2	1				4
(2x y)dxdy				vdudv		du vdv											v							du									4	1			.
			3		3									3					2								2		2	du		3				3
D		*				1		1								1										3					1
	D																					1

Рассмотрим важный частный случай формулы (2.14). Возьмем в качестве новых
переменных полярные координаты точки M x, y . Как известно,
x r cos ,	y r sin ,	(2.16)

где r – полярный радиус ( r 0 ), – полярный угол ( ).

44

Если подынтегральная функция f x, y или уравнение границы области интегрирования содержит сумму x2 y2 , то во многих случаях замена переменных по формулам (2.16) значительно упрощает вычисление интеграла, так как данная сумма в полярных координатах принимает более простой вид: x2 y2 (r cos )2 (r sin )2 r 2 .

Найдем якобиан преобразования (2.16):

x

x

cos

r sin

D(x, y)

r

r(cos

2

sin

2

) r .

D(r, )

y

y

sin

r cos

r

Формула (2.14) принимает вид

f x, y dxdy f (r cos ,r sin )rdrd .

(2.17)

D

D*

Мы получили двойной интеграл в полярных координатах (правая часть равенства (2.17)), который вычисляется путем сведения его к повторному.

Пусть область	D ограничена лучами 1 , 2 и кривыми r r1 ( ) ,			r r2 ( ) ,
причем на отрезке 1 , 2 функции r1 ( ) и r2 ( )			непрерывны и r1 ( ) r2 ( ) . Тогда имеет
место формула
	2	r2	( )
f (r cos ,r sin )rdrd d			f (r cos ,r sin )rdr .	(2.18)
D*	1	r1 ( )
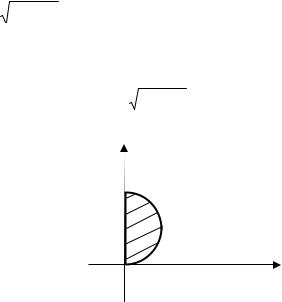
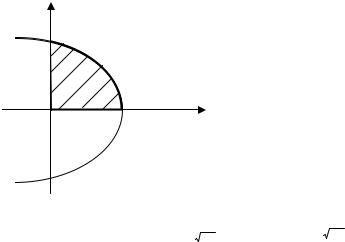
Пример 2.1.4.	Вычислить интеграл	x2 y2 dxdy , где область D		ограничена
	D
линиями x2 y2 2 y , x 0 , ( x 0 ).				x r cos ,
Решение. Область интегрирования D –		полукруг (рис. 2.9). Положим
y r sin и применим формулу (2.17). Так как x2			y2 r 2 , то x2 y2 dxdy	r 2 drd .
			D	D*

Сведем полученный интеграл к повторному, пользуясь формулой (2.18). Уравнение окружности

x2 y2 2 y преобразуется к виду: r 2 sin , а уравнение

прямой	x 0		принимает вид .	Таким	образом,
0			2		2
	,	0 r 2sin (рис. 2.9), т. е.		1 0 ,		,
2					2
r1 ( ) 0 ,		r2 ( ) 2 sin . Согласно формуле (2.18) имеем

y

x 2 y 2 2 y

(r 2 sin )

1 D

О x

Рис. 2.9

															2 sin
			2 sin										r3							8		8
r 2 drd 2 d					r 2 dr 2							(				)d					2 sin3 d		2	(1 cos2 )d (cos )
																				3		3
D*			0		0					0		3			0						0		0
=	8			3				2		8	(1			1)		8		2		16 .
		cos cos
	3		3					0		3				3		3		3		9

45

2.1.6. Приложения двойного интеграла

Рассмотрим некоторые геометрические и физические приложения двойных интегралов. 1. Вычисление объема. Как было установлено п. 2.1.2, объем цилиндрического тела, ограниченного сверху поверхностью z f (x, y) 0 , снизу – плоскостью z = 0, с боков

цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей служит граница области D, вычисляется по формуле

V f (x, y)dxdy ,

D

т. е. с помощью двойных интегралов можно вычислять объемы тел.

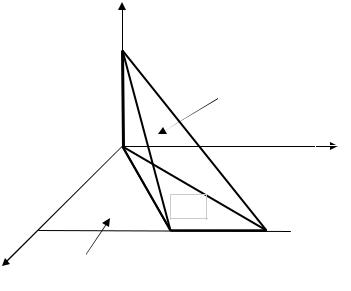
Пример 2.1.6. Вычислить объем тела, ограниченного поверхностями y = x, y = 2x, x + z = 4 (рис. 2.10).

Решение. Имеем

V (4 x)dxdy ,

D

где D –	заштрихованная на рис. 2.10 треугольная область,							ограниченная прямыми y =x,
y = 2x, x = 4. Расставляя пределы интегрирования в двойном интеграле, получаем
V 4 dx	2 x(4 x)dy 4		(4 x) y		2x x dx 4	(4 x)xdx 4	(4x x2 )dx (2x2		x3		4	64		32 .
										)	32
0	x	0	0			0		3			0	3		3
					z
			4
							z = 4 – x
					O
								y

y = 2x

4	D

x	y = x

Рис. 2.10

2. Вычисление площади. Площадь S области D может быть вычислена с помощью двойного интеграла по формуле (см. п. 2.1.2).

S dxdy .

D

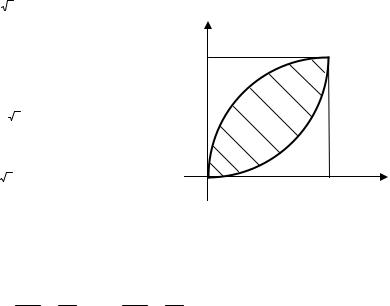
Пример 2.1.7. Вычислить площадь области D, ограниченной линиями y 2 x 1, x y 1 (рис. 2.11).

46

y

	M2
О	1			2	3
				x + y = 1	x
		D
					M1
	y 2 x 1

Рис. 2.11

Решение. Область D представляет собой фигуру, ограниченную слева параболой

y 2 x 1, справа – прямой	y 1 x . Решая		совместно уравнения параболы и прямой,
находим точки их пересечения М1 (3, 2), М2 (0,1) . Следовательно, искомая площадь
	1	1 y	1
S dxdy dy		dx	(2 y y 2 )dy 4,5 .
D	2	y2 1	2

Заметим, что если в данном примере выбрать другой порядок повторного интегрирования (сначала по у, а затем по х), то область D предварительно пришлось бы разбить на две части (осью Оу), так как она ограничена сверху линией, заданной на отрезках1 х 0 и 0 х 3 двумя различными уравнениями. Результат получился бы тот же, но вычисления оказались бы более громоздкими.

3. Вычисление массы пластинки. Рассмотрим на плоскости Оху материальную пластинку, т. е. некоторую область D, по которой распределена масса М с поверхностной плотностью (х, у) . Вычислим по заданной плотности (х, у) массу М этой пластинки,

считая, что (х, у) – непрерывная функция. Разобьем D произвольно на n частей Di (i 1, 2, ..., n) и обозначим через mi массы этих частей. В каждой части произвольно выберем точку (xi , yi ) . Массу mi каждой такой части Di можно считать приближенно равной (xi , yi ) Si , где Si – площадь Di, а масса М всей пластинки приближенно равна сумме

n	n
M mi (xi , yi ) Si ,
i 1	i 1

которая является интегральной суммой для непрерывной функции (х, у) в области D.

В пределе при 0 получим точное значение массы пластинки,	равное двойному
интегралу от функции (х, у) по области D, т. е.
M (x, y)dxdy .	(2.19)
D

47

Пример 2.1.8. Найти массу круглой пластинки радиуса R, если плотность (х, у) в каждой точке М(х, у) пропорциональна квадрату расстояния от точки М до центра круга.

Решение. Выберем систему координат так, чтобы начало координат совпадало с центром круга. Тогда (x, y) k x2 y 2 , где k – коэффициент пропорциональности. По формуле (2.19) имеем:

M k x2 y 2 dxdy ,

D

где областью интегрирования D является круг: x2 y 2 R2 . Переходя к полярным координатам, получаем

2	R	2	r	3		R			3	2	2 kR	3
M k d r rdr k							d kR			d		.
						0
0	0	0	3					3		0	3

4. Вычисление координат центра масс пластинки. Найдем координаты центра масс пластинки, занимающей в плоскости Оху некоторую область D. Пусть (х, у) –

поверхностная плотность в точке М(х, у) , причем (х, у) – непрерывная функция. Разбив область D на части Di (i 1, 2, ..., n) , выберем в каждой из этих частей некоторую точку

(xi , yi ) и будем	считать массу	mi каждой из частей пластинки приближенно равной
(xi , yi ) Si ( Si	– площадь Di	). Если считать, что каждая из этих масс сосредоточена в

одной точке, а именно в точке (xi , yi ) , то для координат xc и yc центра масс такой системы материальных точек получим следующие выражения:

			n				n
x			xi (xi , yi ) Si	, y			yi (xi , yi ) Si
	c		i 1		c		i 1	,	(2.20)
			n				n
			(xi , yi ) Si				(xi , yi ) Si
			i 1				i 1

которые представляют собой приближенные значения координат центра масс пластинки. Чтобы получить точные значения этих координат, необходимо в (2.20) перейти к пределу при 0 . При этом интегральные суммы перейдут в соответствующие интегралы, и мы получим, что координаты центра масс пластинки определяются формулами

	xc	x (x, y)dxdy	, yc	y (x, y)dxdy
		D		D	,	(2.21)
		M		M

где M (x, y)dxdy – масса пластинки.

D

Если пластинка однородная, т. е. (х, упрощаются

	x			xdxdy
		c		D
				dxdy
				D

у) const , то формулы координат центра масс

	, y			ydxdy
		c		D	.	(2.22)
				dxdy

D

48

Величины M y x (x, y)dxdy и M x y (x, y)dxdy в формулах (2.21) называются

D D

статическими моментами пластинки относительно осей Оу и Ох соответственно.

Пример 2.1.9. Найти координаты центра масс однородной пластинки, ограниченной двумя параболами y 2 x и x2 y (рис. 2.12).

Решение. Координаты центра масс данной пластинки найдем по формулам (2.22). Сначала вычислим массу пластинки

M dxdy 1		dx xdy	1 .
D	0	x2	3

Далее вычислим статические моменты ее относительно осей координат:

	M y	xdxdy 1		xdx xdy	3		,
					20
		D	0	x2
	M x	ydxdy 1		dx x ydy		3		.
		D	0	x2	20

Подставляя найденные значения в формулы (2.22), получаем

y

1 у2 х

D

у х2

O

1

x

Рис. 2.12

xc MMy 209 , yc MMx 209 .

5. Вычисление моментов инерции пластинки. Как известно, момент инерции материальной точки относительно некоторой оси равен произведению массы точки на квадрат ее расстояния до этой оси, а момент инерции системы материальных точек равен сумме моментов инерции этих точек.

Пусть область D плоскости Оху занята пластинкой, непрерывная функция (х, у) – поверхностная плотность вещества, распределенного в D. Разбив область D на части Di, площади которых равны Si (i 1, 2, ..., n) , и выбрав в каждой из них некоторую точку

(xi , yi ) , заменим пластинку системой материальных точек с массами mi (xi , yi ) Si и координатами (xi , yi ) . Момент инерции такой системы точечных масс, например,

n

относительно оси Оу равен xi2 (xi , yi ) Si . Примем это выражение за приближенное

i 1

значение момента инерции пластинки. Но оно же представляет собой интегральную сумму для непрерывной функции x2 (x, y) . Переходя к пределу при 0 , получаем для момента инерции пластинки относительно оси Оу следующую формулу:

J y x2 (x, y)dxdy .	(2.23)
D

Аналогично, момент инерции пластинки относительно оси Ох будет определяться формулой

J x y 2 (x, y)dxdy .

D

49

Найдем момент инерции J0 пластинки относительно начала координат. Принимая во внимание, что момент инерции материальной точки с массой m относительно начала координат равен m(x2 y 2 ) , и рассуждая, как и выше, получим

	y															J0	(x2		y 2 ) (x, y)dxdy ,
	y2		1 x														D
																	т. е. J0 J x J y .
	D
								Пример 2.1.10. Вычислить момент инерции плоской
O			1	x
							материальной									фигуры			D,	ограниченной											линиями
							y2	1 x, x 0, y 0									(рис. 2.13), относительно оси Оу, если
							поверхностная плотность (x, y) y .
	Рис. 2.13							Решение. По формуле (2.23) имеем
				1	1 x			1			2	y	2			1 x	1	1			1	x		3		x	4				1	1
		2				2			x									2
J y x			ydxdy dx		x		ydy									dx		x	(1 x)dx														.
											2						2				2					4						24
	D			0	0			0							0			0				3									0

2.2.Тройной интеграл

2.2.1.Определение и вычисление тройного интеграла

Тройной интеграл является непосредственным обобщением двойного интеграла на случай функции трех переменных.

Пусть в некоторой ограниченной замкнутой области трехмерного пространства задана ограниченная функция u f (x, y, z) . Разобьем область Т на n произвольных областей, не

имеющих общих внутренних точек, с объемами V1 , V 2, ..., Vn . В каждой области возьмем произвольную точку M i (xi , yi , zi ) и составим сумму

n
f (xi , yi , zi ) Vi ,	(2.24)
i 1
которая называется интегральной суммой для функции	f (x, y, z) по области Т. Обозначим

через λ наибольший из диаметров частичных областей разбиения.

Определение 2.2.1. Если при 0 интегральная сумма (2.24) имеет предел, который не зависит ни от способа разбиения области Т на части, ни от выбора точек M i , то этот

предел называется тройным интегралом от функции f (x, y, z) по области Т и обозначается одним из символов:

f (x, y, z)dV	или f (x, y, z)dxdydz .
T	T

В этом случае функция f (x, y, z) называется интегрируемой в области Т; Т – областью интегрирования; x, y и z – переменными интегрирования; dV (или dxdydz) – элементом объема.

50