2.2.Миноры и алгебраические дополнения.

Минором M_ij элемента a_ij квадратной матрицы n-го порядка A называется детерминант матрицы (n-1)-го порядка, полученной из матрицы A вычёркиванием i-ой строки и j-ого столбца, на пересечении которых расположен элемент a_ij.

Алгебраическим дополнением (адъюнктом) A_ij элемента a_ij квадратной матрицы A n-го порядка называется его минор, взятый со знаком (-1)^i+j: A_ij=(-1)^i+jM_ij.

Теорема Лапласа (о разложении определителя). Определитель квадратной матрицы равен сумме произведений всех элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам i-ой строки, )

или

(разложение по элементам j-ого столбца, )

Следствие 1. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) этой матрицы равны 0, т.е.

при

Следствие 2. Сумма произведений произвольных чисел b₁, b₂, , b_n на алгебраические дополнения элементов любой строки (столбца) равна детерминанту матрицы, полученной из данной заменой элементов этой строки (столбца) на числа b₁, b₂, , b_n.

Практически определитель раскладывают по элементам строки или столбца, в которых больше всего нулей.

Пример. Вычислить

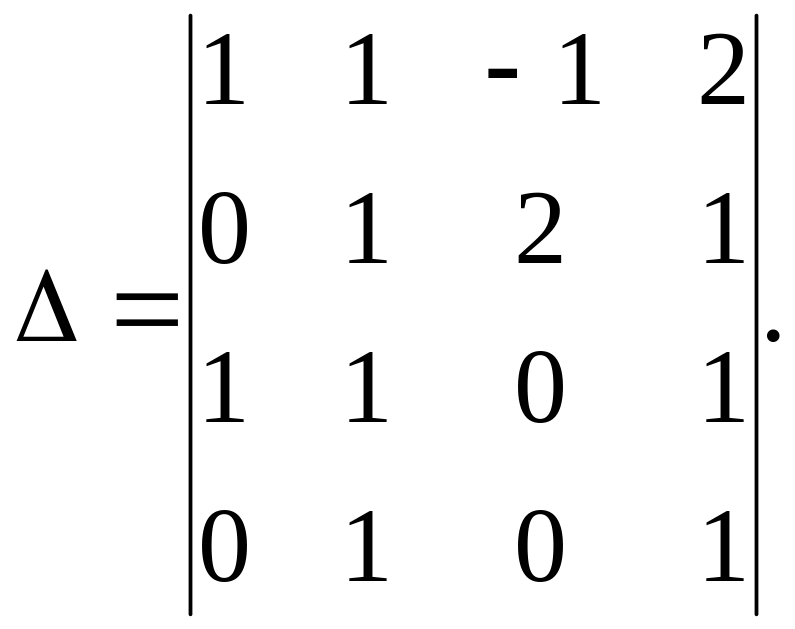
Решение.

Первый способ. Разложим  по элементам четвёртой строки. Вычислим алгебраические дополнения её ненулевых элементов.

Тогда по теореме Лапласа =a₄₂A₄₂+a₄₄A₄₄=1(-3)+11=-3+1=-2.

Второй способ. Разложим  по элементам третьего столбца. Для этого вычислим алгебраические дополнения его ненулевых элементов.

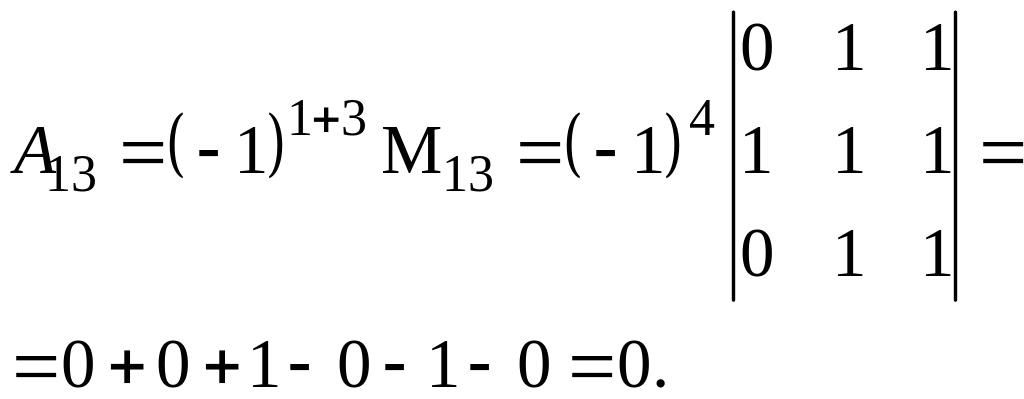
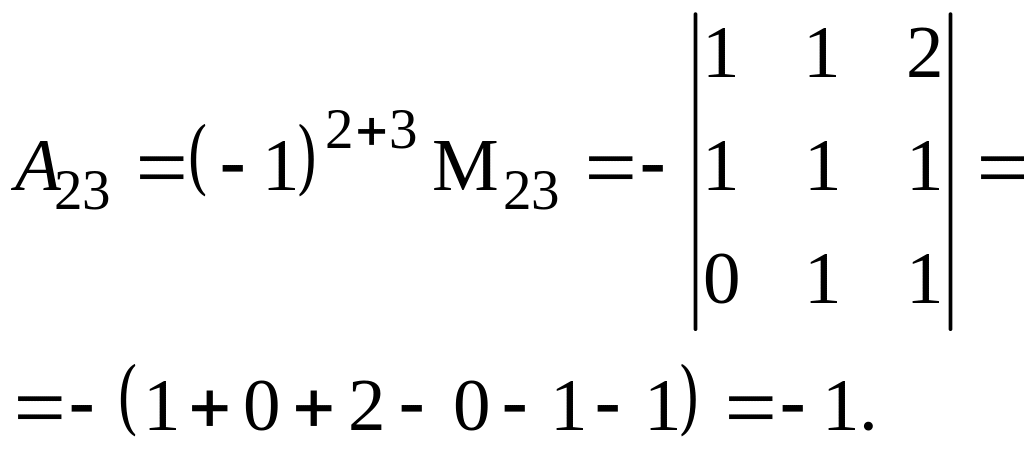
Таким образом, =a₁₃A₁₃+a₂₃A₂₃=(-1)0+2(-1)=-2.

Третий способ. Разложим  по элементам первого столбца. Для этого вычислим алгебраические дополнения его ненулевых элементов.

.

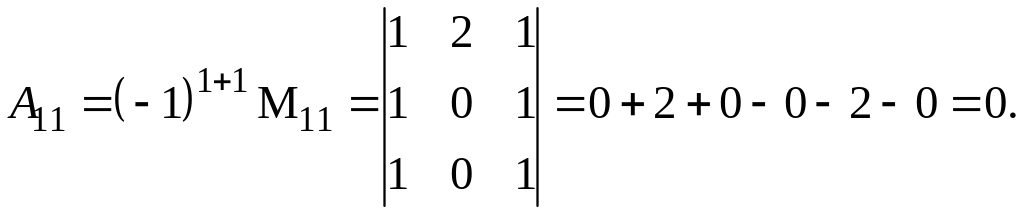
2.3.Свойства определителя n-го порядка.

1. Если какая-либо строка (столбец) матрицы A состоит из одних нулей, то detA=0.

2. При перестановке двух строк (столбцов) матрицы её определитель меняет знак на противоположный.

3. Если матрица A содержит две одинаковые строки (столбца), то detA=0.

4. Общий множитель любой строки (столбца) можно выносить за знак определителя.

5. Если элементы двух строк (столбцов) матрицы A пропорциональны, то detA=0.

6. Линейность детерминанта. Если каждый элемент некоторой строки (столбца) определителя  представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в каждом из которых:

а) все строки (столбцы), за исключением указанной строки (столбца), совпадают с аналогичными строками (столбцами) определителя ;

б) на месте указанной строки (столбца) первый определитель содержит первые слагаемые, а второй – вторые слагаемые данной строки (столбца) определителя .

Пусть i и j меняются от 1 до n. Тогда

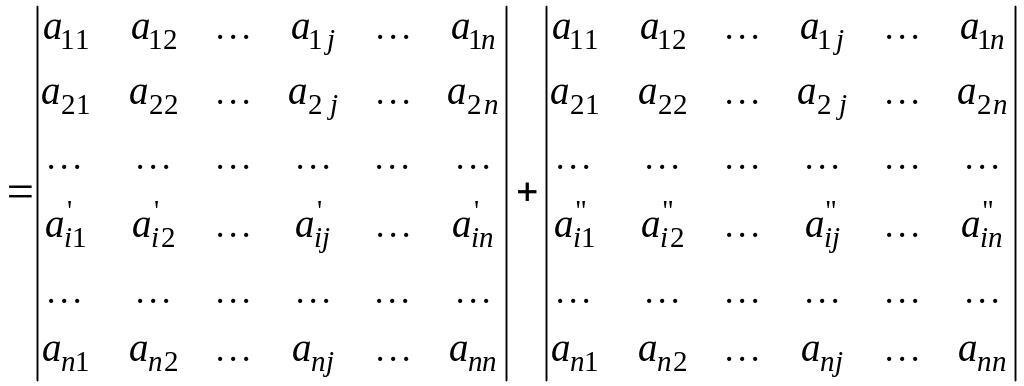или

7. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число

8. detA= detA^Т.

9. Определители треугольных и диагональной матриц равны произведению элементов главной диагонали.

Теорема Лапласа и использование свойств определителя лежат в основе так называемого метода накопления нулей вычисления определителя.

Пример. Вычислим определитель

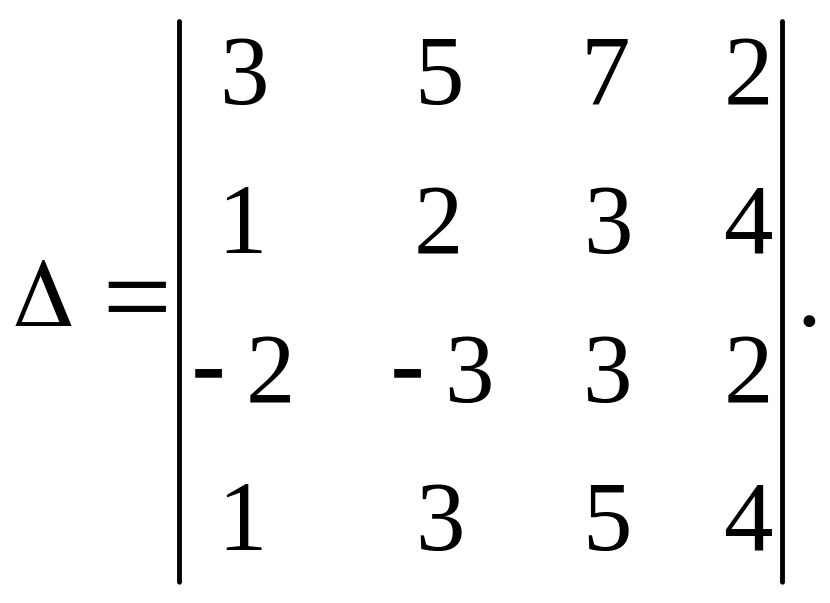
Для этого из первой строки вычтем вторую, умноженную на 3 и запишем результат на место первой строки. К третьей строке прибавим вторую, умноженную на два и запишем вместо третьей строки. Из четвертой строки вычтем вторую и результат пишем на месте четвёртой строки:

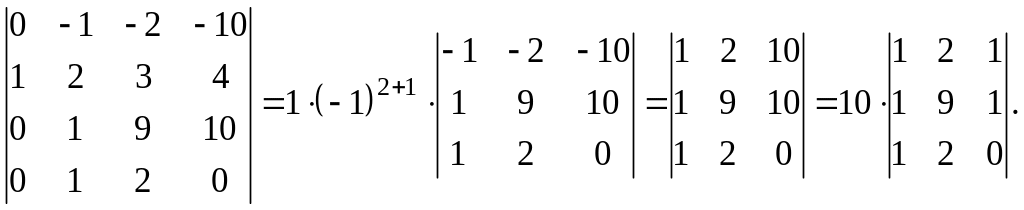
В последнем определителе из второго столбца вычтем первый, умноженный на два и запишем результат на месте второго.