Курсовое проектирование по теории механизмов и механике систем машин

xT , yT – координаты точки M0' встречи толкателя с точкой на про-

филе кулачка;

e, Rmin – соответственно эксцентриситет и минимальный радиус кулачка;

K , K1 , K2 m, n, M0' – точки построения схемы механизма. В дальнейшем будем считать заданными:

1)уравнение центрового профиля кулачка;

2)расстояние а;

3)эксцентриситет е;

4)угловую скорость ω;

5)текущий фазовый угол.

Требуется определить координаты xT , yT точки встречи толкателя

с точкой профиля кулачка	при	повороте последнего	на угол φ,
а также скорость в данный момент.
Определим минимальный радиус. Из рис. 7.18 следует:
R =	e2 +(KK )2 ,		(7.4)
min		1
KK1 = y =		2 px ,	(7.5)
x = а – е.			(7.6)
Подставляя в формулу (7.4) значения (7.5), (7.6), получим
Rmin =	e2 + 2 p(a −e).		(7.7)

Определим на профиле кулачка координаты точки М, которая окажется в контакте с толкателем при повороте кулачка на заданный фазовый угол φ. Для этого необходимо совместно решить уравнение профиля кулачка и уравнение прямой у = kx +b, изображающей положение толкателя в обращенном движении (см. рис. 7.18).

Составим уравнения упомянутой прямой в системе хОу. Угловой коэффициент этой прямой равен tg(90 – φ). Отрезок, отсекаемый на оси Оу (с учетом знака) и равный ОK2 , определяется из следующих условий

(см. рис. 7.18):

nO1 = cose φ;

On = a − nO = a −	e	;	(7.8)
1	cosφ
			231

Стр. 231

ЭБ ПНИПУ (elib.pstu.ru)

отсюда

			e
	b = OK2	= a −		ctgφ.	(7.9)
			cosφ

Тогда уравнение искомой прямой с учетом углового коэффициента и выражения (7.9) примет следующий вид:

		e
	y = xctgφ− a −		ctgφ.
		cosφ

Решаем совместно уравнение (7.10) и уравнение параболы:

	2	= 2 px,
y			e
y	= xctgφ− a −			ctgφ.
			cosφ

Решение системы уравнений (7.11) – это координаты точки М:

(7.10)

(7.11)

yM = ptgφ = p2tg2φ+ 2 p

e

a −

;

cosφ

(7.12)

x = ptg2φ± tgφ

p2tg2φ+

2 p a −

e

+ a −

e

.

M

cosφ

cosφ

Дифференцируя выражения (7.12) по времени, получим:

dxM =

ω1

e

2 ptgφ±

p2tg2φ+ 2 p

a −

+

2

dt

cos

φ

cosφ

ptgφ(ptgφ−esin φ)

+

−esin φ),

2

2

e

p

tg

φ+ 2 p

a

−

cosφ

dy

pω

ptgφ−esin φ

=

±

M

1

1

.

cos

2

e

dt

φ

2

2

p

tg

+ 2 p a −

(7.13)

cosφ

232

Стр. 232

ЭБ ПНИПУ (elib.pstu.ru)

Определим x , y координаты точки				M ' встречи толкателя с точ-
T T				0
кой М на профиле кулачка. В соответствии с рис. 7.18 имеем:
		xT = a − e .				(7.14)
Координату x определим из треугольника O K M '						:
T				1 1	0
y = M '		K =	O M ' 2 − e2 .			(7.15)
T	0	1	1	0

Радиус-вектор O1 M0' = O1 M определим как расстояние между двумя точками М и O1 , координаты которых известны (М ( xM , yM ),O1 (a, 0)):

O M =	(a − x	M	)2 − y2 .	(7.16)
1			M

Подставляя выражения (7.16) в (7.15), получаем:

y	= M '	K =	(a − x	)2 − y2	−e2.	(7.17)
T	0	1	M	M

Дифференцируя (7.17) по времени, получим абсолютную скорость толкателя при повороте кулачка на заданный угол:

dyT

dxM (xM

− a)+ dyM

yM

V =

=

dt

dt

.

(7.18)

T

dt

a2 −e2 − 2axM + xM2 + yM2

Производные

dxM

и

dyM

определяются по формулам (7.13). Диф-

dt

dt

ференцируя по времени выражение (7.18), можно определить ускорение толкателя.

7.10.3. Профилирование кулачковой шайбы для механизмов с плоским толкателем

Для управления станками с ЧПУ при изготовлении кулачковых шайб требуется аналитическое выражение центрового и действительного профилей. Предлагаемый аналитический метод профилирования кулачковых шайб механизмов различных типов позволяет формализовать процесс определения координат профиля в декартовой или полярной системе координат с помощью ЭВМ. Применим данный метод при профилировании кулачковой шайбы с плоским толкателем.

233

Стр. 233

ЭБ ПНИПУ (elib.pstu.ru)

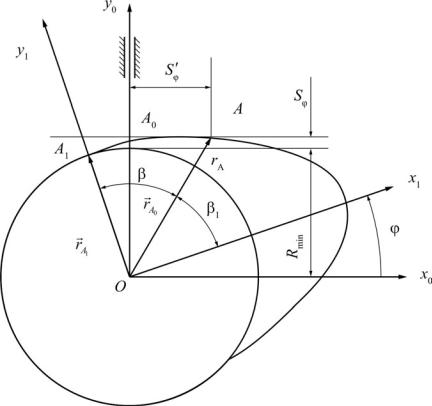
Рассмотрим неподвижную систему координат x0Oy0 и подвижную систему координат x1Oy1 , жестко связанную с шайбой (рис. 7.19). Перемещение системы x1Oy1 относительно x0Oy0 характеризуется поворотом

кулачка на угол φ, при φ = 0 оси систем координат совпадают.

В системе x0Oy0 координаты точки контакта A0 определим радиу- сом-вектором rA0 которому соответствует столбцовая матрица:

	xA0				Sφ'
rA0
	= yA0			= Sφ	+ Rmin .
		1			1

В системе x1Oy1 координаты точки контакта A1 определим радиусом – вектором rA1 с помощью векторного выражения:

rA1 = M10rGA2 ,

где M10 – матрица перехода от системы x0Oy0 к системе x1Oy1 ,

Рис. 7.19. Профилирование кулачковой шайбы для механизма с плоским толкателем

234

Стр. 234

ЭБ ПНИПУ (elib.pstu.ru)

	cosφ		sin φ	0
M10		−sin φ	cosφ	0
	=
		0	0	1

Тогда, согласно определению вектора,

xA				S 'φ cosφ+(Sφ + Rmin )sin φ
	1
rGA1 = yA1			=	−S 'φ sin φ+(Sφ+ Rmin )cosφ .
				1
	1

В полярных координатах радиус-вектор кулачка

r =	x2	+ y2	,
A	A	A
1	1	1

а полярный угол β = π2 −β1 , где β1 – угол, зависящий от координат точки

A1 на профиле кулачка, β1 = arctg(yA1 / xA1 ).

7.10.4. Профилирование кулачковой шайбы для механизмов

столкателем, оканчивающимся острием или роликом

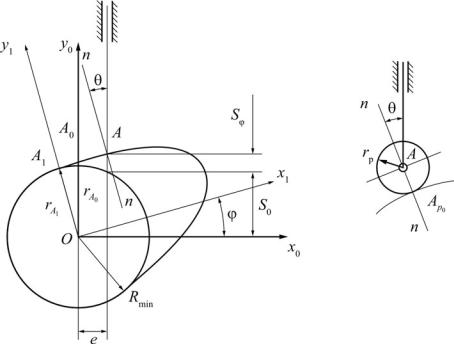
Внеподвижной системе координат x0Oy0 радиус-вектор точки контакта A0 толкателя с шайбой представим столбцовой матрицей (рис. 7.20):

	xA0			e				T
							+ Sφ		,
	rA0 = yA0		= S0	+ Sφ =		e, S0		,1
				1
	1
где S0 – положение толкателя в начале его подъема;
Sφ – текущее перемещение толкателя.
В системе	x1Oy1 координаты точки контакта							A1 определим радиу-
сом-вектором,	rA с помощью матричного выражения:
	1
				T	= M10rA0 =
	rA1 = xA1 , yA1 ,1
			ecos φ + (S0 + Sφ )sin φ
	= M10	−ecos φ + (S0 + Sφ )cos φ						,
					1
где M10 – матрица перехода от системы x0Oy0							к системе x1Oy1 ,
									235

Стр. 235

ЭБ ПНИПУ (elib.pstu.ru)

Рис. 7.20. Профилирование шайбы для механизма с толкателем, оканчивающимся острием

	cosφ		sin φ	0
M10		−sin φ	cosφ	0		,
	=
		0	0	1

xA1 , yA1 – координаты радиуса-вектора rA1 .

Для перехода от центрового к практическому профилю запишем вектор rGAp 0 координат точки Ap0 контакта ролика с действительным про-

филем кулачка в начале подъема толкателя в системе координат x0Oy0 : rGAp 0 = xA0 + rp sin θ, yA0 − rp cosθ,1 T ,

где θ– угол давления, tgθ =	Sφ + e	;
	S0 − Sφ

Sφ – аналог скорости толкателя, Sφ =VqBi ; rp – радиус ролика.

Тогда радиус-вектор точки контакта ролика и практического профиля (точки Ap1 ) в матричном выражении в системе x1Oy1 запишем в ви-

де столбцовой матрицы:

236

Стр. 236

ЭБ ПНИПУ (elib.pstu.ru)

rGAp1

=

= x		, y	Ap1	,1 T	= M	rG		=
		Ap1				10	Ap 0
xA1	+ rp sin (θ−φ)					ecosφ+(S0 + Sφ )sin φ+ rp sin (θ− φ)
yA	+ rp cos(θ−φ) =							−esin φ+ (S0 + Sφ )cosφ− rp (θ− φ)	.
1
		1						1

Для перехода к полярным координатам введем следующие обозначения:

β0 – постоянный угол, β0 = arctg Se0 ;

β1 – дополнительный угол, β1 = arctg yA1 . xA1

Отсюда полярный угол радиуса-вектора β =β0 −β1 . В полярных координатах радиус-вектор кулачка:

r =	x2	+ y2 .
A	A	A
1	1	1

7.10.5.Профилирование кулачковой шайбы для механизма с коромыслом

При профилировании считаем заданными зависимость ψ = f (φ) угло-

вого перемещения выходного звена ψ от угла поворота кулачка φ, а также первую и вторую производные этого перемещения (ψ́,˝),ψдлину коромысла l2 , межосевое расстояние aw , минимальный радиус, радиус ролика rp .

На рис. 7.21 изображены неподвижная система координат x0Oy0 и подвижная система координат x1Oy1 , которые совпадают при φ = 0,

при этом начальное положение коромысла характеризуется значением ψ0 . Повороту кулачка на угол φ соответствует текущее положение

коромысла ψ.

В системе x0Oy0 координаты точки контакта A0 определим радиу- сом-вектором rGA0 , которому соответствует столбцовая матрица:

G	xA0			l		−l		cos(ψ		+ ψ)
					0		2		0	ψ)
rA0	= yA0			=		l2 sin (ψ0 +					.
		1						1

237

Стр. 237

ЭБ ПНИПУ (elib.pstu.ru)

Рис. 7.21. Профилирование кулачковой шайбы для механизма с коромыслом

В системе x1Oy1 координаты точки контакта A1 определим матрич-
ным выражением
		r = M	rG ,
		A	10 A
		1	0
где M10 – матрица перехода от системы x0Oy0				к системе x1Oy1 ,
	cosφ		sin φ	0
M10		−sin φ	cosφ	0
	=				.
		0	0	1

G			cosφ								sin φ				0		l		−l				cos(ψ							+ ψ)
				−sin φ						cosφ					0		0			2							0		ψ)
rA1		=																	l2 sin (ψ0 +															=
				0								0			1									1
				l		−l	2	(		ψ		0	+ ψ)			cosφ+l						2		sin (ψ				0			+ ψ)sin φ
			0	0				(						)			(							2								0			)
				−l	2	cos				ψ		0						−sin φ			)				sin				(		ψ		+	ψ		cosφ
=		l											+ ψ										+ l														=
																			1
	l		cosφ−l					2		cos(ψ				0		+ ψ+ φ)								xA
		0														+ ψ+ φ)								= y			1			.
=		−l		sin φ−l					2		cos(ψ				0											A1
			0
												1													1

238

Стр. 238

ЭБ ПНИПУ (elib.pstu.ru)

В полярной системе координат радиус-вектор текущего положе-

ния точки контакта кулачка и толкателя	r =	x2	+ y2	, а полярный
	A	A	A
	1	1	1

β =β0 −β*.

Для описания практического профиля проводим нормаль к профилю n – n и вводим еще одну систему координат x2 Ay2 с центром в точке А.

В этой системе радиус-вектор, описывающий практический профиль, представим в виде

G	xA		p 2
rAp 2	= yAp 2
		1

	r
		p
	= rp

sin θ

cosθ , 1

где θ – угол давления,

θ = arctg l2 ± Sφ −l0(cos(ψ0)+ ψ). l0 sin ψ0 + ψ

Для представления радиуса-вектора в системе x1Oy1 запишем матричное выражение:

rGAp1 = M10M02rGAp 2 = M12rGAp 2 ,

где M10 , M02 , M12 – матрицы преобразования координат.

Для примера рассмотрим составление матрицы для текущего положения толкателя:

cos(ψ0 + ψ)

M02 = −sin (ψ0 + ψ)0

sin (ψ0 + ψ)	0 X
cos(ψ0 + ψ)	1 Y
		.
0	0 1

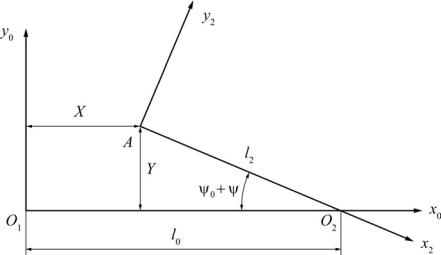
Координаты Х и Y начала координат А системы x2 Ay2 в неподвижной системе x0Oy0 (рис. 7.22) определим так:

X = l0 −l2 cos(ψ+ ψ0 );

Y = l2 sin (ψ+ ψ0 ).

239

Стр. 239

ЭБ ПНИПУ (elib.pstu.ru)

Рис. 7.22. Определение столбца координат подвижной системы координат в неподвижной системе координат

Из матричного выражения получаем матрицу, содержащую координаты практического профиля:

		xA	p 1
rGAp 1
	= y Ap 1			.
		1

240

Стр. 240

ЭБ ПНИПУ (elib.pstu.ru)