
- •3.3. Одномерные задачи.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
- •3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
3.3. Одномерные задачи.
3.3.4.Частица в потенциальной яме
сконечными стенками.
Связанные состояния.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
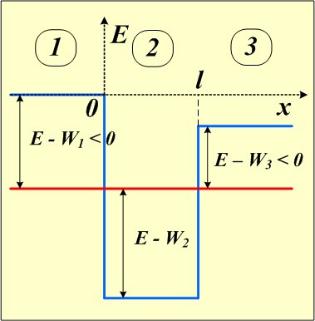
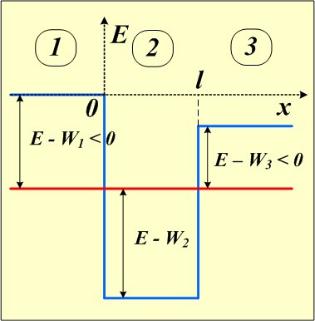
Рассмотрим микрочастицу, которая может совершать одномерное движение. Потенциальная энергия в этой области при x < 0 W = W1, при 0 < x <
L W = W12 а при x > L W = W3.
W1,
W (x) W ,
2W3
x 0,
0x L, x L.
Пусть потенциальная энергия в области 1 равна нулю, а в областях 2 и 3 W2 и W3 соответственно.
0,
W (x) W ,
2W3
x 0,
0x L, x L.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
d 2 n x 2m En W1 n x 0.
dx2 2
В данном случае для областей 1 и 3 величина в скобках
Обозначим |
En W1 0. |
|||||
2m2 En W1 2. |
||||||
|
||||||
Теперь |
|
|
|
|
|
|
d 2 n x |
|
2 |
n x 0. |
|||
|
dx |
2 |
|
|||
|
|
|
|
|
||
Мы получили однородное дифференциальное уравнение с постоянными коэффициентами. Решение этого уравнения имеет вид
x A1 exp 1x A2 exp 2 x ,
где λ1, λ2- корни характеристического уравнения, которое в данном случае
имеет вид
2 2 0.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
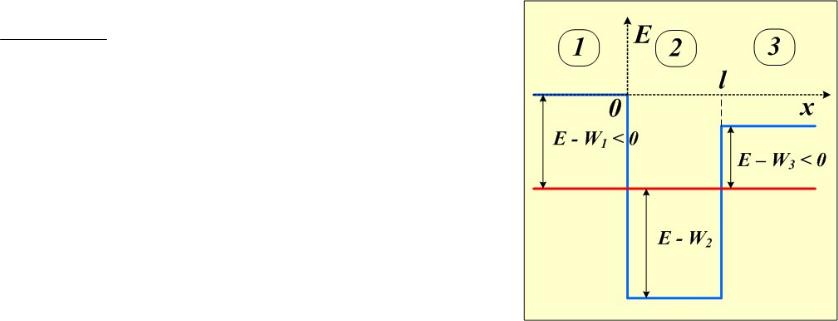
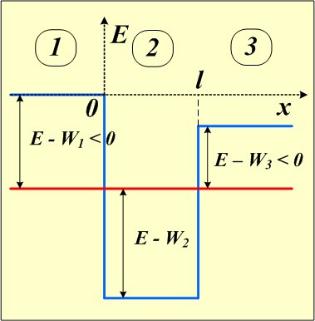
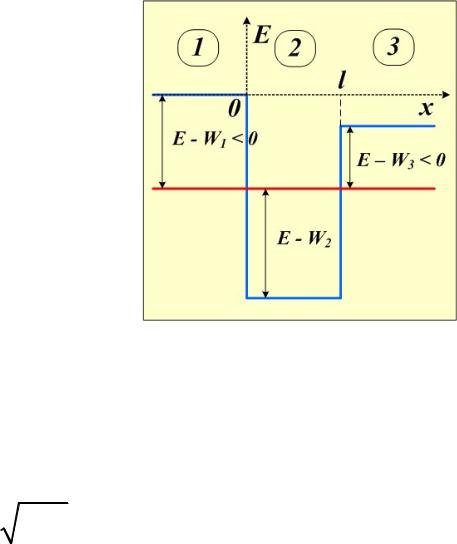
Рассмотрим теперь движение частицы, величина энергии которой соответствует красной линии на рисунке.
Классическая частица с такой энергией будет совершать финитное движение внутри области между x = 0 и x = L.
Чтобы описать движение квантовой частицы, решение уравнения Шрёдингера найдём сначала в отдельных областях 1, 2 и 3, затем потребуем непрерывности волновой функции и её производной на границах областей, в точках x = 0 и x = L.
В данном случае решения уравнения Шрёдингера областях 1, 3 и 2 будут качественно различными. Рассмотрим решения в областях 1 и 3.
|
2 |
ˆ |
ˆ |
|
2m |
n x W n x En n x . |
|
|
|
|
|
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
2 2 0.
Корни характеристического уравнения:
1,2 2 .
2 2m En W1 .
2
|
|
2m |
E W |
2m W E |
n |
. |
|||
1,2 |
|
2 |
n |
1 |
2 |
1 |
|
||
|
|
|
|
|
|
|
|
||
где |
2m |
W1 En |
- действительная величина. |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
Итак, решение дифференциального уравнения
x A1 exp x A2 exp x .
Здесь A1 и A2 – произвольные постоянные.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
|
d 2 n x |
|
|
|
2m |
En W1 n x 0. |
||||
|
dx |
2 |
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
||
Для области 2 2 |
|
|
2m2 |
En W2 0. |
||||||
Теперь |
|
|
|
|
|
|
|
|
|
|
|
|
d 2 n x |
2 |
n x 0. |
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
dx |
2 |
|
||||
|
|
|
|
|
|
|
|
|
||
Мы снова получили однородное дифференциальное уравнение с постоянными коэффициентами. Решение этого уравнения имеет вид
x A1 exp 1x A2 exp 2 x ,
где λ1, λ2- корни характеристического уравнения, которое в данном случае
имеет вид
2 2 0.
1,2 2 .
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
1,2 2 .
Теперь корни характеристического уравнения мнимые
|
|
|
i |
2m E |
n |
W |
ik. |
|
|
1,2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
где k |
2m |
En W2 |
- действительная величина. |
||||
|
2 |
|
|
|
|
|
|
Итак, решение дифференциального уравнения в области 2
2 x B1 exp ikx B2 exp ikx .
Здесь B1 и B2 – произвольные постоянные.
Это решение можно представит в действительной форме
2 x B sin(kx ),
где B и δ – произвольные постоянные.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
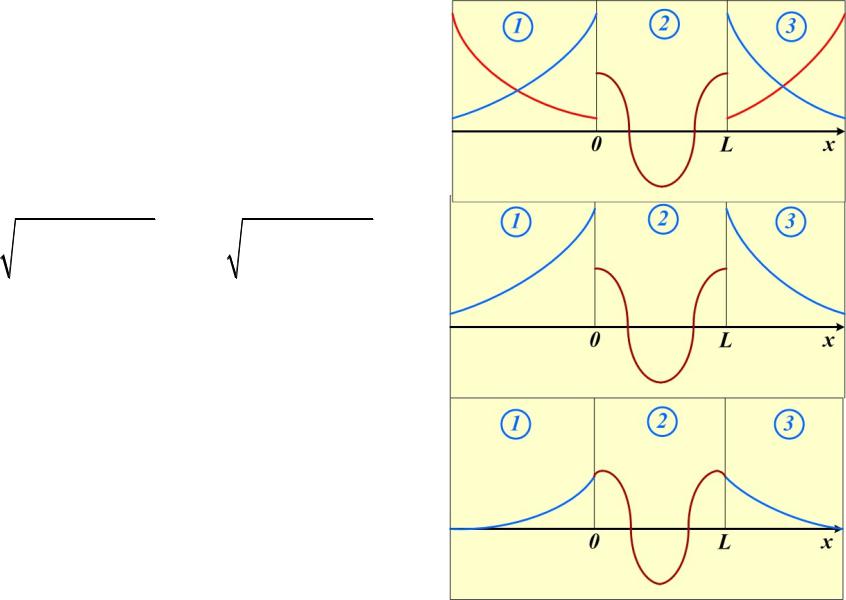
Решения уравнения Шрёдингера в областях 1, 2 и 3:
1 x A1 exp 1x A2 exp 1x ,
2 x B sin(kx ),
3 x C1 exp 3 x C2 exp 3x .
|
2m W E , |
k |
2m E |
W . |
|||
1,3 |
2 |
1,3 |
n |
|
2 |
n |
2 |
|
|
|
|
|
|
||
Исходя из физического смысла волновой функции следует считать, что A2 = 0 и C1
= 0.
После «сшивки» волновая функция должна быть непрерывна вместе со своими производными.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
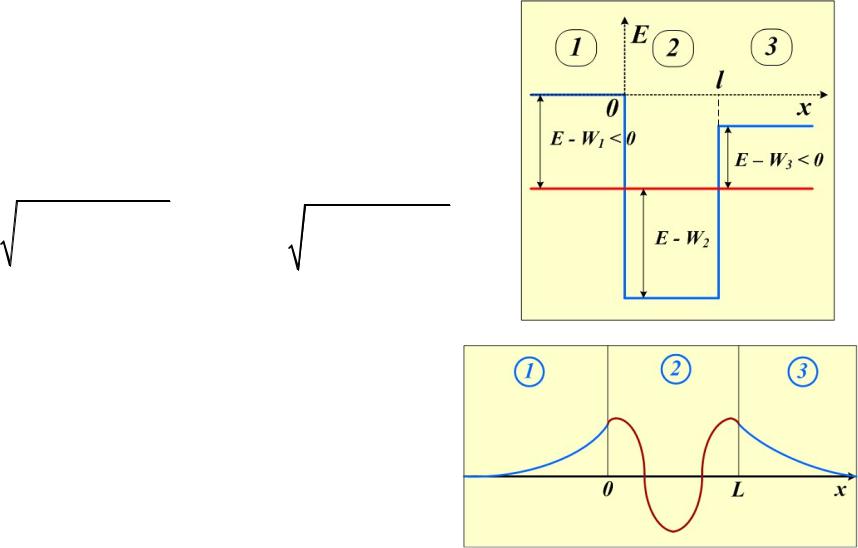
Итак, решения уравнения Шрёдингера областях 1, 2 и 3:
1 x Aexp 1x ,
2 x B sin(kx ),
3 x C exp 3x .
1,3 |
2m2 W1,3 En , |
k |
2m E |
W . |
|
|
|
|
2 |
n |
2 |
|
|
|
|
||
Теперь нам следует записать условия непрерывности волновой функции и её первой производной в точках x = 0 и x = L.
3.3.4. Связанные состояния частицы в потенциальной яме конечной глубины с прямоугольными стенками.
Условия непрерывности волновой функции и её первой производной:
|
1 0 |
|
2 0 |
|
1 |
|
||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
||||||||
|
2 |
L |
|
|
3 |
|
L |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
L |
|
|
|
|
L |
|
|
4 |
|
|
||||
|
|
|||||||||||||||
|
2 |
|
|
|
|
3 |
|
|
|
|
||||||
После подстановки явного вида волновых функций: |
|
|||||||||||||||
Aexp 1 0 |
|
B sin(k 0 ) |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kB cos(k 0 ) |
2 |
|||
1 Aexp 1 0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
B sin(kL ) C exp 3L |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
kB cos(kL ) 3C exp 3L |
||||||||||||||||
