Движение частицы в сферически симметричном потенциале
8. Частица в сферически симметричной
бесконечной прямоугольной потенциальной яме.
Частица находится в бесконечно глубокой потенциальной яме, обладающей сферической пространственной симметрией. Зависимость потенциальной энергии от радиуса выражается формулами:
U (r) 0, |
r a, |
U (r) , |
r a. |
Так как зависимость потенциальной энергии от координат обладает сферической симметрией, решение уравнения Шредингера можно записать в виде
nlm (r, , ) Rnl (r)Ylm ( , ),
где R(r) – радиальная часть волновой функции, а |
Y( , ) – угловая |
(сферические гармоники). |
|
Уравнение Шредингера для радиального решения P(r) = r·R(r) имеет вид:
d 2 P(r) |
|
2 |
|
( 1) |
|
||
dr |
2 |
k |
|
r |
2 |
U (r) P(r) 0. |
|
|
|
|
|
|
|
||
Радиальное уравнение Шредингера для области пространства внутри потенциальной ямы (r < a) имеет такой же вид, как и для свободной частицы:
d 2 P(r) |
|
2 |
|
( 1) |
|||
dr |
2 |
k |
|
r |
2 |
P(r) 0. |
|
|
|
|
|
|
|
||
Решения для области пространства внутри потенциальной ямы (r < a) будем искать в таком же виде, как и для состояний свободной частицы с определенным значением момента импульса:
(1)nlm (r, , ) Akn j (knr)Y m ( , ),
kn 2mEn .
За пределами потенциальной ямы (r > a) значение потенциальной энергии равно бесконечности, поэтому, как и для одномерной потенциальной ямы с бесконечно высокими стенками,
(2)nlm (r, , ) Rnl(2) (r)Ylm ( , ) 0
для любых значений квантовых чисел n, l, m.
На границе областей, в точке r = a должно выполняться условие непрерывности волновой функции.
(1)nlm (a, , ) (2)nlm (a, , ).
Для этого должно выполняться равенство.
Rnl(1) (a) Rnl(2) (a) 0.
Иными словами,
Rnl(1) (a) Akn j (kna) 0.
Для функции P(r) также должно выполняться условие непрерывности:
Pnl(1) (a) Pnl(2) (a) 0,
Pnl(1) (a) Akn j (kna) r 0.
Перепишем условие непрерывности для l = 0 (состояния s-симметрии):
j (kr) |
sin kr |
, |
P |
(1) |
(a) Akn |
sin kna |
a 0. |
|
|
kna |
|||||
0 |
kr |
|
nl |
|
|
||
|
|
|
|
|
|
||
P(1) |
(a) Ak |
n |
sin kna |
a 0. |
nl |
|
kna |
|
|
|
|
|
|
Условие непрерывности выполняется, когда
sin kna 0, kna n ,
kn 2mEn n ,
a
En0
Для l = 1 (состояния
Pnl(1) (a)
p-симметрии):
sin k a
Akn n 2
(kna)
|
2 2 |
n2. |
|
2ma2 |
|
||
|
|
|
|
|
j (kr) sin kr |
cos(kr) , |
|
|
1 |
(kr)2 |
kr |
|
|
||
cos(k a)
n a 0. kna
sin k a
(knan) cos(kna) 0.
tg(kna) kna.
В общем случае условие непрерывности выполняется, если
Akn j (kna) 0,
то есть, если j (kna) 0.
Значения ka, удовлетворяющие последнему равенству, являются корнями сферических функций Бесселя. Они известны и их значения приведены в таблице.
Состояние |
cnl |
Состояние |
cnl |
1s |
3,142 |
2s |
6,283 |
1p |
4,493 |
1f |
6,988 |
1d |
5,763 |
2p |
7,725 |
В общем случае решение имеет вид
kn 2mEn an ,
2 2 .
En n
2ma2
Движение частицы в сферически симметричном потенциале
9. Частица в сферически симметричной
прямоугольной потенциальной яме конечной глубины.
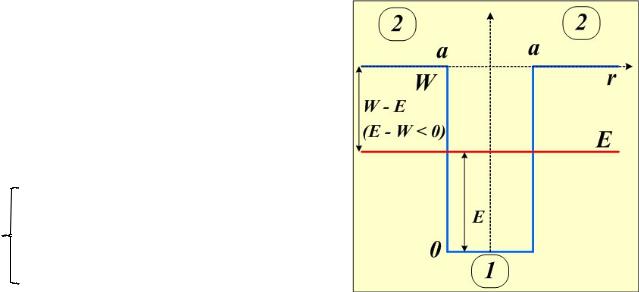
Частица находится в потенциальной яме конечной глубины W, обладающей сферической пространственной симметрией. Зависимость потенциальной энергии от радиуса выражается формулами:
U (r) 0, |
r a, |
U (r) W , |
r a. |
Так как зависимость потенциальной энергии от координат обладает сферической симметрией, решение уравнения Шредингера можно записать в виде
nlm (r, , ) Rnl (r)Ylm ( , ),
где R(r) – радиальная часть волновой функции, а |
Y( , ) – угловая |
(сферические гармоники). |
|
Уравнение Шредингера для радиального решения P(r) = r·R(r) имеет вид:
d 2 P(r) |
|
2 |
|
( 1) |
|
||
dr |
2 |
k |
|
r |
2 |
U (r) P(r) 0. |
|
|
|
|
|
|
|
||
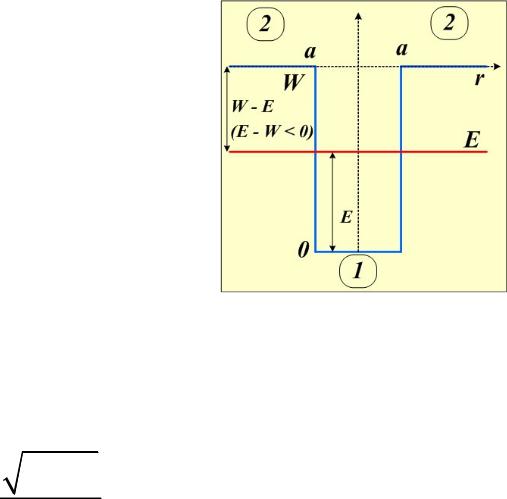
Радиальное уравнение Шредингера для области пространства внутри потенциальной ямы (r < a), где потенциальная энергия частицы равна нулю, имеет такой же вид, как и для свободной частицы:
d 2 P(r) |
|
2 |
|
( 1) |
|||
dr |
2 |
k |
|
r |
2 |
P(r) 0. |
|
|
|
|
|
|
|
||
Решения для области пространства внутри потенциальной ямы (r < a) будем искать в таком же виде, как и для состояний свободной частицы с определенным значением момента импульса:
(1)nlm (r, , ) Akn j (knr)Y m ( , ),
kn 2mEn .
За пределами потенциальной ямы (r > a) значение потенциальной энергии равно W, поэтому, как и для одномерной потенциальной ямы со стенками конечной высоты, существуют два класса решений - для значений энергии частицы E > W (пролётная частица) и для E < W (частица, захваченная ямой).