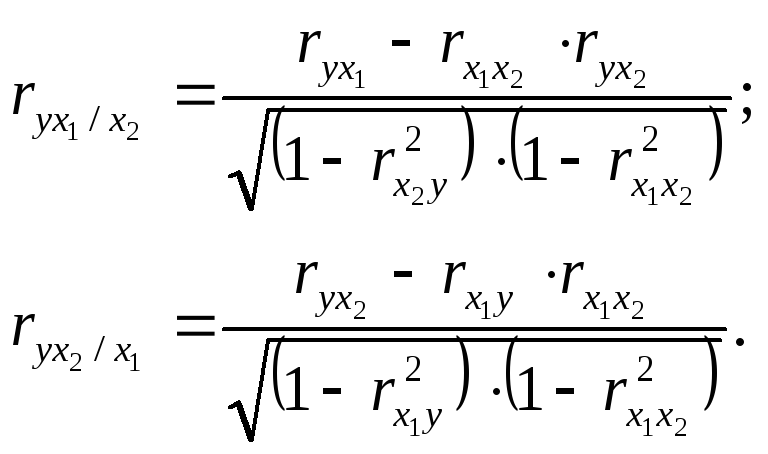9.6 Собственно-корреляционные параметрические методы изучения связи. Оценка существенности корреляции

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторов.

Линейный коэффициент корреляции был впервые введен в начале 1890-х гг. Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента:

.

(9.18)

где

линейный коэффициент корреляции.

Используя математические свойства средней и формулу (9.18), получим:

(9.19)

Дальнейшие преобразования позволяют получить следующую формулу линейного коэффициента корреляции:

, или,

(9.20)

где

число наблюдений.

Произведя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:

.

(9.21)

или

.

(9.22)

Коэффициент корреляции может быть выражен через дисперсии слагаемых:

.

(9.23)

Формулы (9.21), (9.22), (9.23) применяются при изучении совокупностей малого объема ().

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой

(9.24)

где		коэффициент регрессии в уравнении связи;
		среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Легко доказывается, что условие является необходимым и достаточным для того, чтобы величинык были независимы. При этом условии коэффициенты регрессии,также обращаются в нуль, а прямые регрессии по и по оказываются взаимно перпендикулярными (параллельными: одна оси абсцисс, а вторая оси ординат).

Если же , то это означает, что все точки (,) находятся на прямой и зависимость между и является функциональной. Прямые регрессии в этом случае совпадают. Указанное положение распространяется также на случай нормального распределения трех и более величин.

Линейный коэффициент корреляции изменяется в пределах от - 1 до 1: . Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в табл. 9.3.

Значимость линейного коэффициента корреляции проверяется на основе -критерия Стьюдента. При этом выдвигается и проверяется гипотеза () о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется-статистика:

.				(9.25)
	Таблица 9.3
	Оценка линейного коэффициента корреляции
	Значение линейного коэффициента связи	Характер связи	Интерпретация связи
		Отсутствует	-
		Прямая	С увеличением увеличивается
		Обратная	С увеличением уменьшается, и наоборот
		Функциональная	Каждому значению факторного признака строго соответствует одно значение результативного признака

При выполнении -статистика имеет распределение Стьюдента с входными параметрами:.

Если расчетное значение (табличное), то гипотезаотвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости междуи.

Данный критерий оценки значимости применяется для совокупностей .

При большом числе наблюдений () используется следующая формула-статистики:

.

(9.26)

Для статистически значимого линейного коэффициента корреляции можно построить интервальные оценки с помощью -распределения Фишера:

.

Первоначально определяется интервальная оценка для по выражению

,

(9.27)

где		табулированные значения для нормального распределения, зависимые от (- уровень вероятности);
		табличные значения, -распределения. Функция- нечетная, т.е..

В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.

Эмпирическое корреляционное отношение рассчитывается по данным группировки, когдахарактеризует отклонения групповых средних результативного показателя от общей средней:

,

(9.28)

где		корреляционное отношение;
		общая дисперсия;
		средняя из частных (групповых) дисперсий;
		межгрупповая дисперсия (дисперсия групповых средних).

Все эти дисперсии являются дисперсиями результативного признака.

Теоретическое корреляционное отношение определяется по формуле:

,

(9.29)

где		дисперсия выравненных значений результативного признака, т.е. рассчитанных по уравнению регрессии;
		дисперсия эмпирических (фактических) значений результативного признака.

Тогда

,

(9.30)

объясняется влиянием факторного признака.

В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е.

(9.31)

при изучении степени коррелированности факторов отражает вариацию результативного признака () под влиянием всех не учтенных при анализе факторов, т.е. носит остаточный характер:

Отсюда формула корреляционного отношения принимает вид

.

(9.32)

Корреляционное отношение изменяется в пределах от 0 до 1 (), и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (см. табл. 9.3).

Теоретическое корреляционное отношение также может вычисляться по формуле

.

Корреляционное отношение является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

Для измерения тесноты связи при множественной корреляционной зависимости, т.е. при исследовании трех и более признаков одновременно, вычисляются множественный, или совокупный, и частные коэффициенты корреляции.

Множественный коэффициент корреляции рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.

Он вычисляется по формуле

где		множественный коэффициент корреляции;
		теоретических значений результативного признака, рассчитанная по уравнению множественной регрессии;
		остаточная дисперсия;
		общая дисперсия результативного признака.

В случае оценки связи между результативным () и двумя факторными признаками () и () множественный коэффициент корреляции можно определить по формуле

.

(9.33)

где

парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции можно рассчитать, используя парные коэффициенты и коэффициенты регрессии в стандартизованном масштабе ():

где

коэффициенты в стандартизованном масштабе.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

Приближение к единице свидетельствует о сильной зависимости между признаками. При небольшом числе наблюдений величина коэффициента множественной корреляции, как правило, завышается.

Чтобы оценить общую вариацию результативного (моделируемого) признака в зависимости от факторных признаков, величина коэффициента множественной корреляции корректируется на основании следующего выражения:

(9.34)

где		скорректированное значение;
		число наблюдений;
		число факторных признаков.

Корректировка не производится при условии, если

Проверка значимости коэффициента множественной корреляции осуществляется на основе -критерия Фишера-Снедекора:

(9.35)

Гипотеза о незначимости коэффициента множественной корреляции () отвергается, если.

Оценка доверительных границ производится следующим образом: величина приравнивается к гиперболическому тангенсу величины, т.е., где

Плотность распределения является почти нормальной со средним значением

(9.36)

и дисперсией

Следовательно,

отсюда:

(9.37)

По таблицам -преобразования Фишера находят и, т.е. - верхняя и нижняя границы значений.

Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признакамии при фиксированном значении других () факторных признаков, т.е. когда влияниеисключается и оценивается связь междуив «чистом виде».

Коэффициент, в котором исключается влияние только одного факторного признака, называется коэффициентом частной корреляции первого порядка. В общем виде коэффициент корреляции первого порядка выражается так:

.

В случае зависимости от двух факторных признаковикоэффициент частной корреляции следующий:

(9.38)

где

парные коэффициенты корреляции между указанными в индексе переменными.

В первом случае исключено влияние факторного признака , во втором- . Значения парного и частного коэффициентов корреляции отличаются друг от друга, так как парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный - учитывает наличие и влияние других факторов.

Проверка значимости и расчет доверительных интервалов для частных коэффициентов корреляции аналогичны расчетам для парных коэффициентов с тем лишь отличием, что число степеней свободы определяется как

где

порядок коэффициента частной корреляции.

Обобщенную методику корреляционного метода анализа экономических явлений и процессов можно представить блок-схемой (рис. 9.8).