
- •Лекция 2 Геометрический метод решения злп с двумя переменными.
- •1. Геометрический смысл злп с двумя переменными
- •2. Различные случаи решения злп с двумя переменными
- •§ 4. Системы линейных уравнений и выпуклые множества
- •1. Базисные решения системы линейных уравнений
- •2. Выпуклые множества в n – мерном пространстве и допустимые базисные решения злп
2. Различные случаи решения злп с двумя переменными
При геометрическом решении ЗЛП возможны следующие случаи:
Опорная прямая
 соприкасается с областью М в единственной
точке. Тогда ЗЛП имеет единственное
оптимальное решение
соприкасается с областью М в единственной
точке. Тогда ЗЛП имеет единственное
оптимальное решение иmin
иmin .
.
Опорная прямая
 имеет с областью М общий отрезок прямой.
Тогда ЗЛП имеет бесконечное множество
решений иmin
имеет с областью М общий отрезок прямой.
Тогда ЗЛП имеет бесконечное множество
решений иmin .
.Область М – неограниченная сверху (справа), и при уменьшении линия уровня
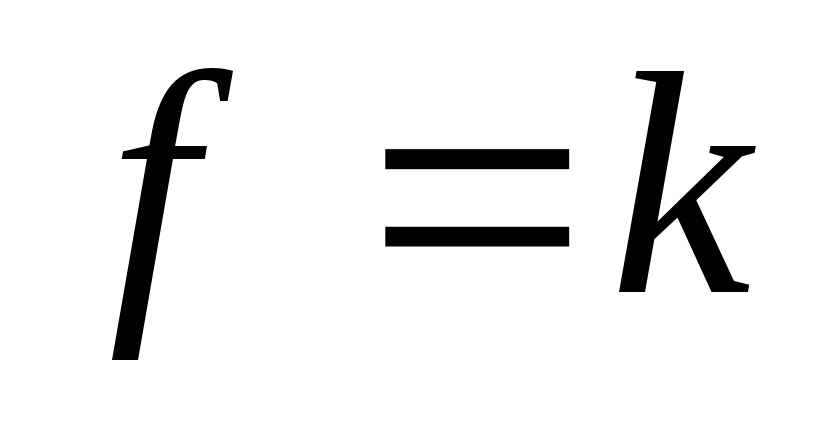 движется вверх (вправо). Следовательно,
уровень функции
движется вверх (вправо). Следовательно,
уровень функции может уменьшаться сколько угодно иmin
может уменьшаться сколько угодно иmin .
Это означает, что ЗЛП не имеет оптимального
решения. Задача не будет иметь решения
и в случае
.
Это означает, что ЗЛП не имеет оптимального
решения. Задача не будет иметь решения
и в случае .
.
Пример 1. Дать геометрическое истолкование и решить упражнение 2 к §1.
Решение. Область ограничений в упражнении может быть задана в стандартной форме:

Среди
неотрицательных решений этой системы
неравенств нужно найти такое, которое
минимизирует функцию
![]() .
.
Выбрав
систему координат
![]() ,
построим область ограничений (Рис. 3.7).
Возьмем линию уровня
,
построим область ограничений (Рис. 3.7).
Возьмем линию уровня![]() ,
тогда
,
тогда![]() .
Вектор
.
Вектор![]() показывает, что при увеличении
показывает, что при увеличении![]() линия уровня
линия уровня![]() движется влево и вниз, и первое
прикосновение, как видно из рис.3. 7,
движется влево и вниз, и первое
прикосновение, как видно из рис.3. 7,

Рис. 3. 7
с
областью М произойдет в точке пересечения
прямых ![]() и
и ![]() .Это точка
.Это точка
![]() .
Значит оптимальным решением является
решение
.
Значит оптимальным решением является
решение![]() иmin
иmin![]() .
.
В
исходной задаче требовалось найти max![]() .
Как было отмечено ранее, оптимальное
решение будет таким же, поэтомуmax
.
Как было отмечено ранее, оптимальное
решение будет таким же, поэтомуmax![]() =
=![]() .
.
2. Рассмотрим ЗЛП с той же системой ограничений:

но
с другой целевой функцией
![]() .
Требуется найти допустимое решение
системы неравенств, которое минимизирует
эту функцию.
.
Требуется найти допустимое решение
системы неравенств, которое минимизирует
эту функцию.
Линии
уровня функции
![]() параллельны
прямой
параллельны
прямой![]() .
Поэтому опорная прямая
.
Поэтому опорная прямая![]() пройдет по границе области ограничений
М (по отрезку прямой
пройдет по границе области ограничений
М (по отрезку прямой![]() ),
т.е. оптимальных решений у этой задачи
бесконечное множество. Одно из них
),
т.е. оптимальных решений у этой задачи
бесконечное множество. Одно из них![]() ,
иmin
,
иmin![]() .
.
Пример 3. Найти неотрицательное решение системы неравенств:

и
минимизирующее линейную функцию
![]() .
.
Область
допустимых решений ограничена тремя
прямыми L![]() ,
L
,
L![]() и L
и L![]() ,
определяющими полуплоскости решений
первых трех неравенств и является
неограниченной сверху и справа. Линия
уровня
,
определяющими полуплоскости решений
первых трех неравенств и является
неограниченной сверху и справа. Линия
уровня
![]() при уменьшенииk
будет перемещаться вправо, а, значит,
min
при уменьшенииk
будет перемещаться вправо, а, значит,
min![]() и данная задача оптимального решения
не имеет.
и данная задача оптимального решения
не имеет.

Рис. 3. 8
Мы видим, что геометрическое истолкование ЗЛП приводит к ее решению. Из рассмотренных примеров видно, что если ЗЛП имеет оптимальное решение при n=2, то одним из ее оптимальных решений являются координаты вершины (угловой точки) многоугольника допустимых решений системы ограничений задачи, в которой целевая функция имеет экстремум.
Таким же образом можно решить ЗЛП в канонической форме, в которой число переменных n больше количества уравнений m на 2. Тогда можно выбрать две переменные, остальные переменные и целевую функцию выразить из уравнений (как в примере с задачей 1 из §1) через них, затем решить графически ЗЛП с двумя переменными.
Аналогично можно истолковывать решение ЗЛП при большем числе переменных. При количестве переменных n=3 множество допустимых решений системы ограничений задачи геометрически представляет многогранную неограниченную выпуклую область или выпуклый многогранник, и одним из оптимальных решений задачи, если они существуют, будут координаты вершины (угловой точки) этого выпуклого многогранника (или многогранной области), в которой достигается экстремум целевой функции. При n>3 может быть сохранена геометрическая терминология, но решать ЗЛП графически уже невозможно.
