ГОС математика / Геометрия / 10,11,12

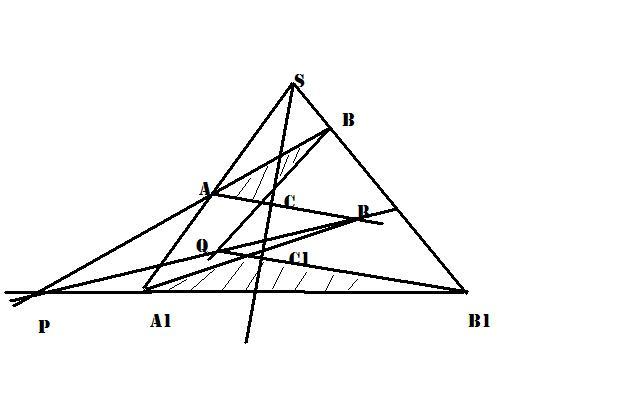
Вопрос 10. Проективная плоскость. Теорема Дезарга. Опр. Проективной пл-ю Р^2 наз. некот-е множ-во точек, определенные подмнож-ва кот-х наз. прямыми и кот-е удовл. след-м аксиомам: Любым двум различ. точкам одна и только одна прямая. Любым различным прямым одна и только одна точка. ∃4 точки никакие три из которых не лежат на одной прямой. Опр. Два трехверш-ка АВС и А^1В^1С^1имеют центр персп-вы,если AA^1∩BB^1∩CC^1=S Опр. Два трехверш-ка имеют ось персп,если их соотв стор пересек в 3 точках,леж на одной прям. Теор Дезарга. Если два тр-ка имеют центр перспективы, то они имеют ось перспективы. Дано: Δ АВС,ΔА^1В^1С^1 AA^1∩BB^1∩CC^1=S – центр перспективы, AB∩A^1B^1=P , AC∩A^1C^1=R , CB∩C^1B^1=Q P,R,Q инц-ны одной прямой Данная конфигурация сод-т 10 точек и 10 прямых и наз-ся конфигурацией Дезарта. Каждые 3 точки инцид-ны одной прямой. По малому принц двойств имеем:10 прям инц-ны одной точке. Ч/з каждую точку проходит 3 прямые. Любая из 10 точек м/т выступать в качестве центра перспективы. Док-во: 1)Расс-м Δ АВС, ΔА^1В^1С^1 в аффинном пр-ве и не лежащие в одной пл-ти. Имеем: (АВС), (А^1В^1С^1) Эти две пл-ти имеют общ точку Р= AB∩A^1B^1.Если две пл-ти имеют общ точку, то они ⋂ -ся по прямой,проходящей ч/з эту точку. Точки Р,Q,R∈(АВС) ∩(А^1В^1С^1) ⇒∈одной прямой⇒для простр-но расп-х Δ эта теор док-на. 2)Теперь рас-м теор в случае, когда треуг лежат в одной пл-ти. Рас -м точку S^1,не леж в пл-ти œ, и проведем прямые S^1A,S^1B,S^1C На прямой SS^1 возьмем точку S^2 и соед. её прямыми с точками А^1,В^1,С^1. Прямые S^1A и S^2A леж в одной пл-ти,кот-я м/б опр-на прямыми SS^1 и SA^1⇒S^1А ⋂S^2A^1=А^0 Аналогично получ,что S^1В ⋂S^2В^1=В^0, S^1С ⋂S^2С^1=С^0,Пл-ть треуг А^0В^0С^0 обозначим ч/з œ^0. Пусть œ ⋂œ^0=m Δ АВС и ΔА^1В^1С^1лежат в разных пл-х и имеют центр перспективы-точку S^1.Их осью персп явл m. AB∩A^0B^0=P , AC∩A^0C^0=R , CB∩C^0B^0=Q. Точки Р,Q,R∈m. Δ АВС и ΔА^0В^0С^0также лежат в разных пл-х и имеют ось перспективы-точку m. AB∩A^1B^1 в некот пл-ти œ. Но A^1B^1 имеет с пл-ю œ^0 ед-ю общ точку P , ⇒A^1B^1∩A^0B^0=Р. Аналогично AC∩A^1C^1=R , CB∩C^1B^1=Q. Точки Р,Q,R∈m.Теор док-на. Теор обратная теор Дезарга. Если два тр-ка имеют ось перспективы, то они имеют и центр перспективы. Д-во следует непосредственно из малого принципа двойственности (всякое верное утверждение об инцидентности точек и прямых проективной пл-ти останется верным, если в нем слово «точка» заменить словом «прямая» или наоборот). Модели проект пл-ти 1. Афинно-проек пл-ть(А^2 ∪a ∞) 2.Связка прямых и плоскостей 3. 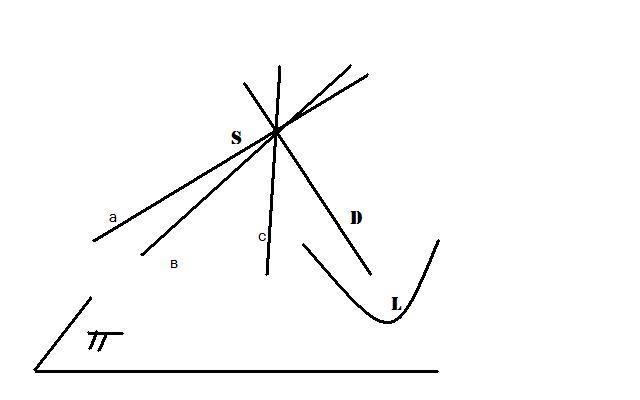Ариф-я проект-я пл-ть В А^3выберем произв точку S и все возможные прямые – это и есть связка прямых и пл-й. Точками – наз прямые связки Прямыми – пл-ти связки. Чтобы утв-ть,что это есть модель проект пл-ти, надо пок-ть,что вып акс.(1.двум точк инц одна и только одна прям. 2.двум прям инц-на одна и только одна точка. 3. сущ-ет 4 точки общ полож-я) Установим соотв м/у эл-ми первых двух моделей А^2 ∪a ∞=π аА= a ⋂ π SBВ œ l=œ⋂ π (S,c)c Опр.Две модели наз изоморф, если м/у их соотв эл-ми уст-но взаим однознач соотв и сохр инц-ть точек и прям.

Вопрос 11. Аксиоматический метод построения геометрии. «Начала» Евклида. Система аксиом Гильберта. В основе построения аксиоматического метода лежат: 1) вводят неопределяемые (основные) понятия; 2) основные отношения (лежать на, между, равенства); 3) формулируют аксиомы (постулаты)-утверждения, принятые без доказательств, об указанных понятиях, связанных некоторыми отношениями. Все остальные факты получаются из них путем логических рассуждений и называются следствиями из аксиом (теоремами, леммами, предложениями). Аксиоматический метод построения геометрии впервые был выделен Евклидом. Заслуги Евкл: 1.Школьн учеб были основ по начала Евкл. 2.Все извест-е матем и ученые придерж схемы Евкл(акс метод) 3. Книга Евкл была 1-м дошедш до наш врем изд-ем,в кот обоснов-ся геом. Требования к системе аксиом: 1.Независимость.(ни одна из аксиом не является следствием остальных, в противном случае эту аксиому можно перенести в список теорем, т.е. доказать) 2.Непротиворечивость (в системе аксиом не должно быть аксиомы и ее отрицания, это требование является обязательным, в противном случае для любой теоремы можно доказать ее отрицание, а такая теория не может иметь применения) 3.Полнота (если к аксиомам нельзя добавить независимую от них аксиому, то система аксиом считается полной). Постулаты 1.От всякой точки до всякой точки можно провести прямую. 2.Огр-ю прямую можно непрерывно продолжить 3.Из всякого центра и всяким раствором может быть описан круг. 4.Все прямые углы равны. 5.Если при пересечении 2-х прямых 3-ей, сумма внутре одностор углов меньше двух прямых, то эти прямые пересекаются. Аксиомы 1.Равные одному и тому же равны между собой. 2.Если к равным прибавляются равные, то и целые будут равны. 3.Если от равных отнимаются равные, то и остатки равны. 4.Если к неравным прибавляются равные, то и целые неравны. 5.Удвоенное одного и того же равны между собой. 6.Половину одного и того же равны между собой. 7.Совмещающиеся друг с другом равны между собой. 8.Целое больше части. 9.И две прямые не содержат пространства(через 2 точки проходит не более одной прямой). Предложение 1.На данной ограниченной прямой можно построить равносторонний треугольник 2.От данной точки отложить прямую, равную данной прямой 3.Из 2-х данных нервных прямых от большей отнять прямую, равную меньшей. 4. 1-й признак равенства треугольников (по 2м сторонам и углу между ними) 5. В равнобедренном треугольнике углы при основании равны. Доказательство 5. 1. Продолжим АС до прямой АD. 2. Отложим от В прямую, равную CD (BM=CD). 3. ώ(B,BM)∩AB=F => CD=BF 4. ΔDBA=ΔFCA (1 признак: угол А-общий, по А2 AF=AD, AB=AC). => угол BDC=CFB. 5. ΔBCD=ΔBCF (F=D,BF=CD,BD=FC)=> угол BCF=CBD. => угол ABC=ACB (A3) 5 постулат Особый интерес вызвал 5 постулат. Известны многочисленные попытки доказательства 5 постулата. Все они не увенчались успехом, в док-х явно или неявно исп-сь утв-я, эквив ему, кот-е сами док-ся с его исп-ем. В школьн учеб вместо 5 постулата исп-ся акс пар-ти: через точку вне прямой в пл-ти, задаваемой точкой и этой прямой можно провести не более одной прямой, пар-й данной. То, что через точку можно провести прям, пар-ю данной, док-ся без 5 постулата. Ед-ть такой прямой принимают в кач-ве акс или исп-т эквив-е утв-е. Гильберт опубликовал книгу «Основания геометрии» , в которой изложил 5 групп аксиом, все 3 требования к аксиомам выполняются. Акс. соед-я(принадлежности). 1.Для любых 2-х точек А и В существует прямая а, принадлежащая каждой из этих точек. 2.Для любых 2-х точек существует не более одной прямой, принадлежащей этим точкам.(единственность). 3.На прямой существует по крайней мере 2 точки. Существуют 3 точки, не лежащие на одной прямой. 4.Для любых 3-х точек, не лежащих на одной прямой, существует плоскость, принадлежащая каждой из этих точек. В плоскости существует, по крайней мере, одна точка. 5.Для любых 3х точек , не лежащих на одной прямой , существует не более одной плоскости, принадлежащей этим точкам. 6.Если 2 точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. 7.Если 2 плоскости имеют общую точку, то они имеют по крайней мере еще одну общую точку. 8.Существует по крайней мере 4 точки, не лежащие в одной плоскости. Следств. В любой плоскости существует, по крайней мере, 3 точки. Док-во: Пусть есть плоскость ά. 1).∃ А∈ ά.(по акс 1.4) 2).∃В не принадлежащая ά.(1.8) АВ(1.1) 3)∃С ∉ АВ (1.1) 4)∃бэтта=(АВС) (1.4.) 5)∃D∈альфа ⋂ бэтта.(1.7) 6)∃Е∉ бэтта (1.8.) , ∃ гамма =(АВЕ) (1.5) 7)∃F∈ альфа ⋂ гамма (1.7) A,D,E.- искомые Акс. порядка (отнош-е м/у) 1. Если А лежит между В и С, то А лежит также между С и В и А, В, С-различные точки одной прямой. 2.Для любых точек А и В существует точка С, что В лежит между А и С. 3.Из 3-х точек прямой не более одной лежит между двумя другими. 4.Аксиома Паша. Если прямая а лежит в (АВС), не проходит через его вершины и пересекает одну из его сторон во внутренней точке, то она пересечет покрайней мере одну из его сторон. Теор4. Для любых 2х точек А и С существует точка D, лежащая между ними. Теор5. Из 3х точек прямой одна и только одна лежит между двумя другими. Акс конгруэнт-ти, (равенства) 1.Для любого отрезка АВ и любого луча h с вершиной А1 на h существует В1: АВ=А1В1 2.Если 2 отрезка равны 3-му, то 1-ый равен третьему. 3.Аксиома сложения отрезка. Если В лежит между А и С, В1 между А1 и С1, АВ=А1В1, ВС=В1С1, то АС=А1С1. 4.Пусть даны угол h,k и луч h1 в некоторой плоскости, тогда в данной полуплоскости относительно прямой, содержащей луч h1 существует луч k1 , такой, что угол h1k= h1 k1 5.Даны 2 треугольника ΔАВС=ΔА1В1С1. Если АВ=А1В1, АС=А1С1, угол ВАС= В1 А1С1, то угол АВС= А1В1С1. Акс непрерывности 1(Архимеда)Каковы бы ни были отрезки CD и АВ найдется такое натуральное число n, что n*СD>AB 2(Кантора) Если есть система вложенных отрезков, причем для любого отрезка эпсилонт существует такое число n, принадлежащее N такое, что АnBn<эпсилонт

Вопрос 12. Геометрия Лобаческого, основные факты, непротиворечивость. В основе геом. Лобачевского лежат 4 группы аксиом абс-ой геом-ии {принад-ти, порядка, рав-ва, непрерывности) и аксиома Лобачевского. Теория построена Аксиоматиче-м методом если: перечисляются основные понятия: основные объекты и осн-е отнош-я. формулируются аксиомы в кот-х сообщаются некот. св-ва основ-х понятий, достаточных для построения геометр. теории. все понятия, кот-е не являются основными д/б опр-ны ч/з основные понятия и понятия ранее определённые. все предложения (утв-я) кот-е не явл-ся акс. д/б доказаны ч/з аксиомы или ранее док-е предложения. Акс. Лобачевского: ∃прямая а и точка А, не принадл-я а, что в пл-ти, опред-й точкой и прямой ч/з точку А проходит более одной прямой, не пересек-х прямую а. 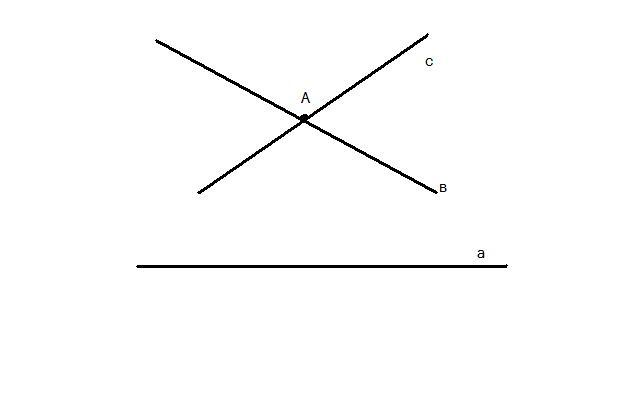∑ЛОБ= ∑ АБС∪() Все утв-я абсолют. геом. справедливы и в геом. Лобач. Не сложно показать, что утв-е сформ-е в аксиоме выполняется и для любой другой пары точки и прямой. => пятый постулат => аксиома парал-ти => противоречие, т.е. верно для любой пары. Теор1. Через точку не принадлежащую данной прямой в плоскости, определяемой этой точкой и прямой проходит бесконечно много прямых, не пересекающих данную прямую. 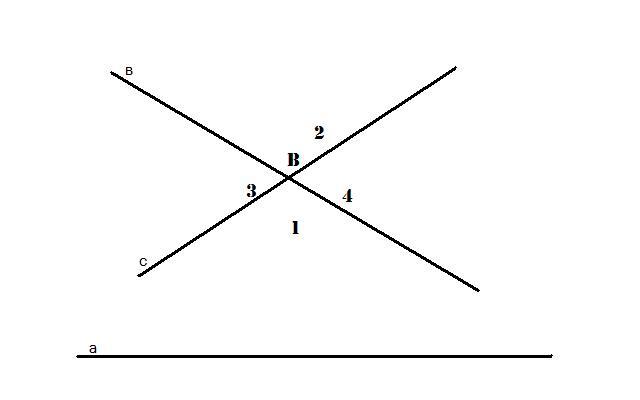Док-во: Из акс Лобач⇒ч/з В проходит по крайней мере две прям в и с: а ⋂ в=а ⋂ с= Прямые в и сразбив пл-ть на две пары вертик углов1,2 и 3,4 Т.к прямые в и с не пересек а,то а∈одному из углов1,2,3,4.Пусть а∈верт углу 1. В этом случае любая прям про-т ч/з В и леж в паре 3,4 не пересек прям а. Таких прямых бесконечно много. Ч.т.д. Теор2. Если прям ВВ^1 пар-на прям АА^1в некот точке С,то она пар-на прямАА^1 и в др своей точке. Теор3.Ч/з точку ∉прям АА^1,в пл-ти опр-й этими точками и прямой в напр АА^1 про-т точно одна прям пар-ая прям АА^1 Теор4.Если прямая АА^1 пар-на ВВ^1в некот напр,то и ВВ^1 пар-на АА^1в этом же напр. Св-ва пар-х прям: 1. Если 1-я прямая пар-на 2-й,а 2-я пар-на 3-й в одном и том же направлении,то 1-я пар-на 3-й в том же направлении. 2. Расс-е м/у паралл-ми прям стрем-ся к 0 в стор пар-ти и в бесконеч в противополож стор. Опр. Две прямые не явл-ся паралл-ми и пересек-ся назыв-ся сверхпараллельными. Теор Л1. Сумма внутр углов любого Δ <2-х прямых углов Теор Л2. сумма внутр углов любого Δ непостоянна Теор Л3. Сумма внутр угл прост 4-х уг-ка<4d Теор.(4 признак рав-ва треуг-ов, по 3 углам)Если 3 угла одного треуг. соответственно равны 3 углам другого треуг., то такие треуг равны. 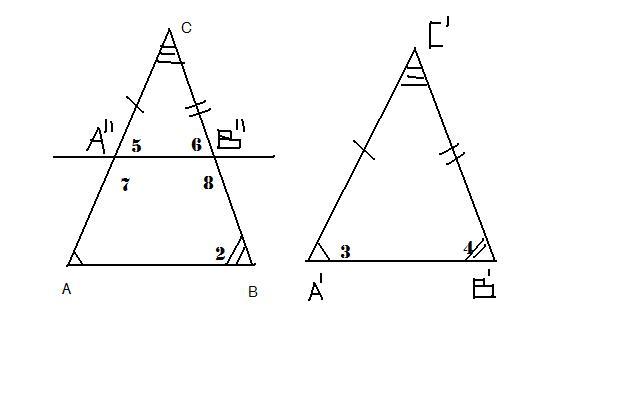Док-во: Угол А=А^1;угол В=В^1;угол С=С^1 Если АС=А^1С^1,то треуг = по 2-му призн (стор и 2-м прилеж. углам) АС не =А^1С^1,например АС>А^1С^1 1)А^11 ∈[СА):СА^11=С^1А^1 2)В^11 ∈[СВ), СВ=С^1В^1 3)А^11В^11 4) ΔА^11В^11С= ΔА^1В^1С^1(по 1-му призн) ⇒угол 3=5, угол 4=6 5)угол 1=5,угол 2=6 6) ΔАВС и А^11В^11 А^11В^11 ⋂АВ=,т.к. 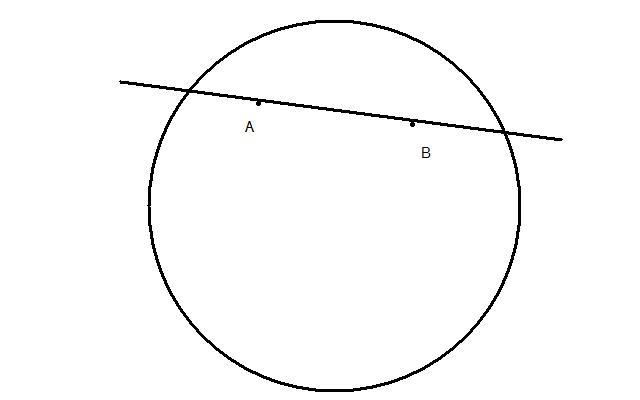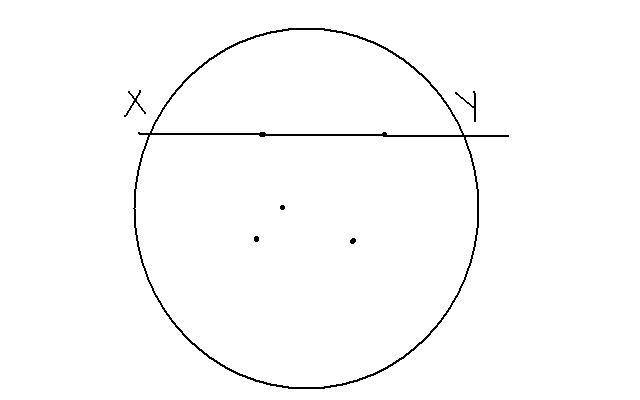1=5 А^11В^11 не ⋂АВ, по акс Паша(Если прямая а лежит в (АВС), не проходит через его вершины и пересекает одну из его сторон во внутренней точке, то она пересечет покрайней мере одну из его сторон) В11 лежит м/у В и С 7)S(АВВ^11А^11)=угол 1+2+8+7=угол 5+6+8+7=(5+7)+(6+8)=2d+2d=4d Получили противоречие с Л3(сумма внутр угл прост 4-х уг-ка<4d ) ⇒наше предпол-е, что АС не =А^1С^1не верно ⇒треуг равны. Непр-ть Опр. Сист акс наз-ся непротиворечивой, если из этой сист нельзя вывести некот-е непротив-е друг другу утвержд. Теория наз. непрот-й, если она построена на базе непрот-х акс. 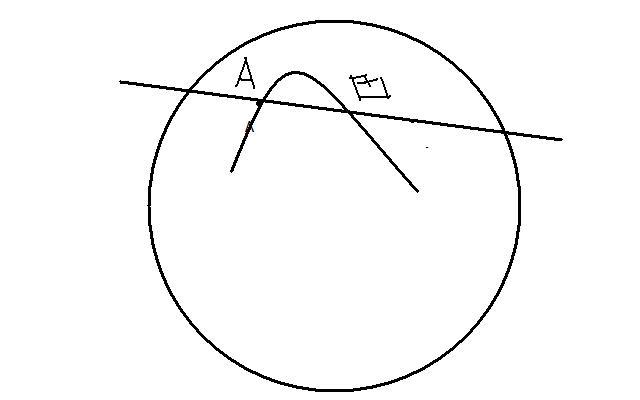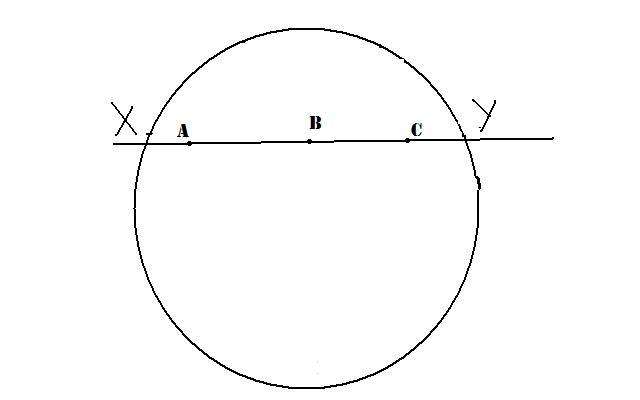Модель Кэли-Клейна Расс-м обычную Евклидову пл-ть, в пл-ти расс-м окр-ть На мн-ве L определим осн понят и отнош,исп-е в акс. Так б/т постр модель пл-ти Лобач Е2:А-абсолют,L-внутр точки(обл-ть) Точка модели – любая точка ∈L Прямая модели – любая хорда окр. без гранич точек. Принад-ть - обыч евкл отнош принадл. Отнош-е лежать м/у: точка Р лежит м/у А и В,если Р леж м/у А и В в обыч евкл смысле. Два отрезка(угла) конгруэнтны, если существу движение отображающее один отрезок(угол). Выполнимость акс 1,2,5 группы 11.Для люб 2-х точек∃ прям и только одна 12.Ч/з люб 2 различ точки проходит прямая и притом только одна. 13.На люб прям ∃ 2 точки, 3 точки общ полож. 21.Если В лежит м/у А и С ⇒ А,В,С-леж на одной прям,и В леж м/у С и А. 22.Для люб А,В∈L, ∃С:В лежит м/у А и С. 23. Для люб 3-х одной прям,не >1 точки леж м/у двумя другими. 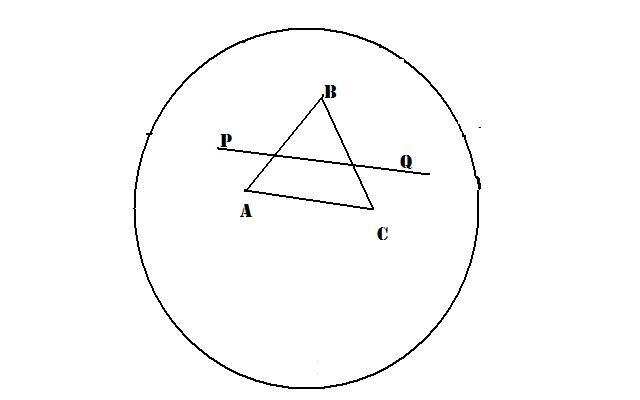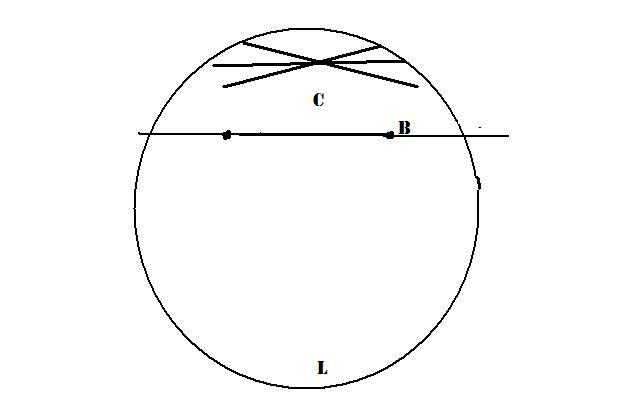24.Акс Паша 5.Акс Лобачевского