ГОС математика / Геометрия / 1,2,3
.doc|
Вопрос 1. Построения на плоскости циркулем и линейкой. а) Решить задачу на построение - описать способы построений, проводимые некоторыми абстрактными инструментами по определенным правилам. I.Анализ – поиск решения задачи. Делают чертеж (набросок) от руки, проводят доп построения, устанавливают связи м/у элементами искомой фигуры и данными фигурами, выявляют цепочку основных построений, выполнение которых приводит к искомой фигуре. (считаем, что задача решена, анализируем её, ищем необ-мые элементы). II.Построение – выполняем основные построения, порядок которых определен анализом (опираясь на аксиомы и базовые задачи). III.Доказательство. Доказываем, что построенная фигура искомая, т.е. удовлетворяет всем требованиям задачи. IV.Исследование – выясняет, всегда ли задача имеет решение и сколько ещё решений она имеет при различном выборе данных фигур. б) Аксиомы абстрактной линейки (с помощью нее можно проводить бесконечные прямые) и абстрактного циркуля (им можно проводить окружности любого радиуса). А1. Через две данные точки можно провести прямую и притом только одну. А2. Любым данным радиусом можно провести окружность с центром в данной точке. А3. Можно выбирать точки, принадлежащие или не принадлежащие данным или построенным фигурам. Базовые задачи:
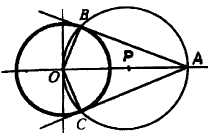
в) Методы решения задач: Метод пересечения множеств Строятся точки, удов-щие опр-ным усл-ям. ! положение некоторой точки М опр-ся усл-ми a и b, тогда рассмотрим фигуру Фа, Состоящую из всех точек, обладающих св-вом а, и фигуру Фb, состоящую из всех точек с условием b. Тогда точка М должна принадлежать обеим фигурам. Т.е. она принадлежит пересечению этих фигур. Пример 1(метод пересечения) Построить кас-ную к данной окр-ти через данную точку, находящуюся вне круга, ограниченного данной окр-тью. И Анализ.
! прямая, проходящая через точку А,
касается окр-ти в точке В. Радиус ОВ
перпен-рен прямой АВ. В этом случае
отрезок ОА виден из точки В под прямым
углом Построение. 1) Разделим ОА пополам (известное построение), Р - середина ОА. 2) Проведем окр-ть с центром Р и радиусом РА (А2). 3) Отметим точки В и С пересечения окр-тей (А3). 4) Проведем прямые АВ и АС (А1). Построения закончены. Теперь покажем, что проведенные прямые удовлетворяют усл-ю задачи. Док-во.
Прямая АВ (АС) перпен-рна радиусу окр-ти
ОВ (ОС), т.к. АВО
(АСО)
опирается на диаметр ОА окр-ти Иссл-е. Так как построенная окр-ть проходит через внутреннюю точку О данной окр-ти и внешнюю точку А, то окр-ти перес-ся в двух точках. Задача имеет два решения. Одно решение, если точка А лежит на окружности. Решений нет, когда А внутри окружности. Алгебраический метод Если даны какая-то фигура или отрезки (их длины), то удобно искомый отрезок обозначить x и, используя св-ва данных фигур или которые надо построить, составить алг-е ур-ние или сист. ур-ний. Пример 2. (алгебраический метод) П Анализ. ! задача решена и MN – искомая прямая. MN||AC,
тогда
S∆MBN=
S∆AMNC
или
S∆MBN=1/2
ABC; ∆MBN~∆ABC (по
1му
признаку)
=>
Вывод: отношение S – ей подобных треугольников равно квадрату коэффициента подобия.
Пусть ВМ=х, АВ=с k=x/c; ½=k2; ½ = x2/c2 => x2 = c2/2; x = c/√2; x = c√2/2. Построение. 1 2.
M,
M 3. MN, MN||AC MN – искомая Док-во: ∆MBN~∆ABC (по 1му признаку)
г) Задачи неразрешимые циркулем и линейкой. Тh
Гаусса-Ванцеля: прав-ный
n-угольник
возможно построить циркулем и линейкой
1 Пусть
а
- ребро данного куба, х
– ребро куба с удвоенным объёмом,
тогда По
критерию разрешимости
Решение задачи Платоном (4в.до н.э.) с помощью двух прямых подвижных углов. Архимед с помощью циркуля и линейки со вставкой. 2. Трисекция угла. Разделить данный угол на 3 равные части. В частных вариантах эта задача разрешима циркулем и линейкой. Невозможно разделить цирк-м и лин-ой угол 600. Эта задача равносильна построению прав-го 18-угольника, впис-го в окр-ть. На основании Тh Гаусса построить такой 18-уг-к невозможно. 3. Квадратура круга. Построить квадрат, S которого = S данного круга. r-радиус
круга, х
– сторона квадрата. Тогда Задача
свелась к новой задаче на построение
отрезка |
Вопрос 2. Многоугольник. Площадь мн-ка. Равновеликость, равносоставленность многоугольников. Теорема Бояи-Гервина. а) Опр. Ломанной линией наз.сов-ть отрезков А1А2,А2А3,…Аn-1 Аn, Аi – вершины ломаной, А1А2,…-звенья. Опр. Ломаная прямая наз. простой, если любые два смежных звена не лежат на одной прямой. Опр. простая ломаная линия наз.замкнутой, если ее начало совпадает с концом. Опр: Многоугольник — это геом. фигура, определяемая как замкнутая ломаная (без самопересечения). Вершины ломаной называются вершинами многоуг-ка, а отрезки — сторонами многоуг-ка. Площадь многоуг-ка: !М:=некоторый многоуг-к
Расс-м
Q
– мн-во всех мног-ков,
то S(M)=S(M1)+S(M2);
Эти условия явл-ся аксиомами площади многоуг-ка. б) Площадь треугольника
Док-во:
Д Расс-м ср.линию DE, DE∩AH=F, AF = FH = n/2 Опустим перпен-ры из точек C и B на прямую DE, получим прямоуг-к CMNB, кот. состоит из трапеции CDEB, ∆CMD и ∆BNE.
С
др.стороны:
н
По
акс.1, из этих равенств получаем:
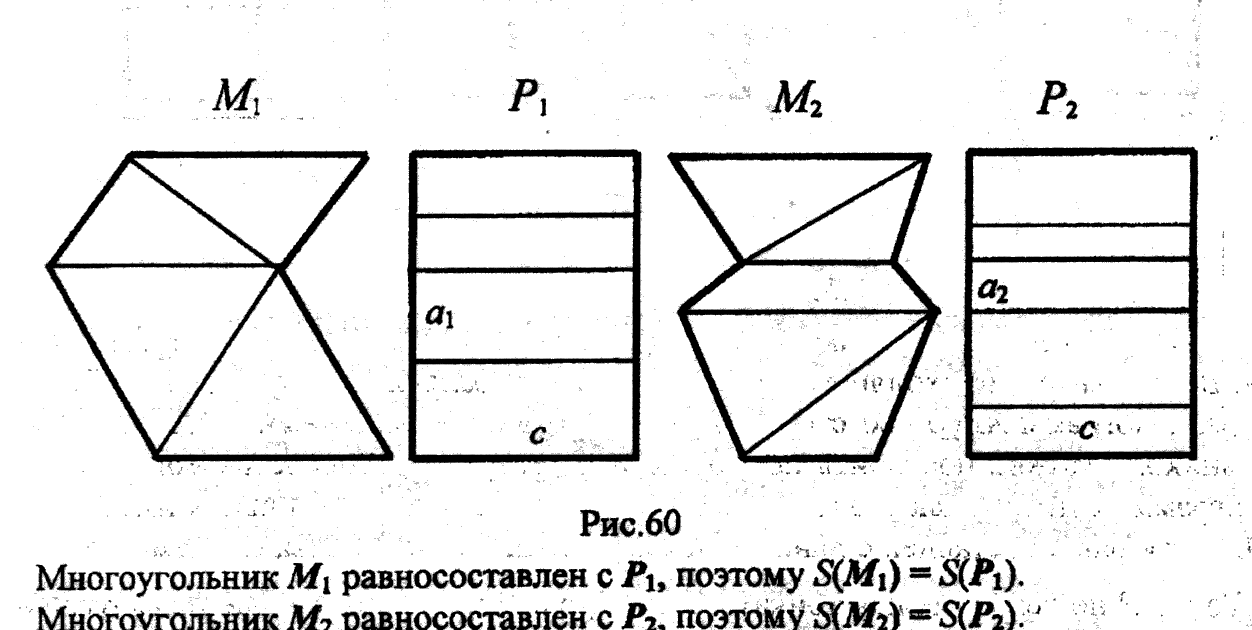
в) Опр: Мног-ки наз. равновеликими (р/в), если они имеют одинак-е площади. Опр: Если мног-к М1 можно разбить на мног-ки A1,…,An а мног-к M2 на мног-ки B1,…,Bn и A1=B1,…,Bn=An, то мног-ки M1 и М2 наз-ся равносоставленными (р/с). По акс.2: равносост-е мног-ки явл-ся равнов-ми. Справедливо и обратное утв-е. ЛЕММА 1: Если мног-к М равносоставлен с мног-ми М1 и М2, то М1 и М2, - равносост-е. ЛЕММА 2: Дан прямоуг-к с измерениями a и b. Можно построить равносост-й с ним прямоуг-к с данной стороной c, большей a и b. ТЕОРЕМА Бояи-Гервина: Всякие равнов-е мног-ки равносост-е. Док-во: Даны два равнов-х мног-ка М1 и М2, S(М1)= S(М2). Разобьем мног-ки М1 и М2 на треуг-ки. Для каждого треуг-ка построим равносост-й с ним прямоуг-к. Выбираем отрезок c, равный наиб-й из сторон всех прямоуг-ков, и для каждого прямоуг-ка построим равносост-й с ним прямоуг-к со стороной c (см.рис). Тогда все прямоуг-ки, полученные из многоуг-ка М1 можно сложить в прямоуг-к P1 со сторонами c и a1, а из всех прямоуг-ков, относящихся к М2, можно составить прямоуг-к P2 со сторонами c и a2.
М1 равносост-н с P1=>S(M1)=S(P1) М2, равносост-н с P2=>S(M2)=S(P2)
Т.к.
S(M1)=S(M2),
S(P1)=
c * a1,
S(P2)=
c * a 2
,
то
Значит,
прямоуг-ки Т.о.
По
лемме 1: |
Вопрос 3. Линии второго порядка. Линии на пл-ти задаются урав-ми F(x,y)=0. Линия состоит из всех точек, коорд-ты которых (x,y) удовл-ют этому ур-нию. Опр: Линия G наз-ся алгебраической 2го порядка если она имеет вид:
Совершая || -ный перенос, поворот, осевую и цент-ную симметрии, линия 2го порядка примет вид невырожденной линии (эллипс, гипербола, парабола) или вырожденной (мнимый эллипс, точка, пара прямых), вырож-е интереса не вызывают, поэтому рассм-м только невырожденные и исследуем их каноническое урав-е: Опр: Эллипс – мн-во точек пл-ти, сумма расстояний от которых до двух фикс-ных точек(фокусов) - величина постоянная, большая чем расстояние м/у фокусами.
Каноническое ур-ние:
Опр: Парабола – мн-во точек пл-ти, равноуд-х от фикс-ной точки (фокуса), и фикс-ной прямой (директрисы), не прох-щей ч/з фокус. Каноническое ур-ние:
Oпр:
Гипербола
– мн-во точек пл-ти, разность расстояний
от кот. по абсол. вел-не до двух данных
точек Каноническое ур-ние:
Док-во ур-ния гиперболы: G - кривая гиперболы Строим в системе коор-т. Расстояние м/у фокусами обозначим через 2c, c>a. О – середина F1F2, F1F2 принад.ОХ.
Т
Возводим обе части в квадрат:
Возводим обе части в квадрат:
Так как с > a, то c2 – a2 >0. Пусть
c2
– a2
= b2,
тогда
Разность расстояний от любой точки, квадраты кот. удовл-ют этому ур-нию, до фокусов, по модулю равна 2a. Иссл-е ур-ния гиперболы: A1, A2 - вершины гиперболы. A1A2 =2a – действ-я ось гиперболы A1O=OA2 – действ-е полуоси
2)
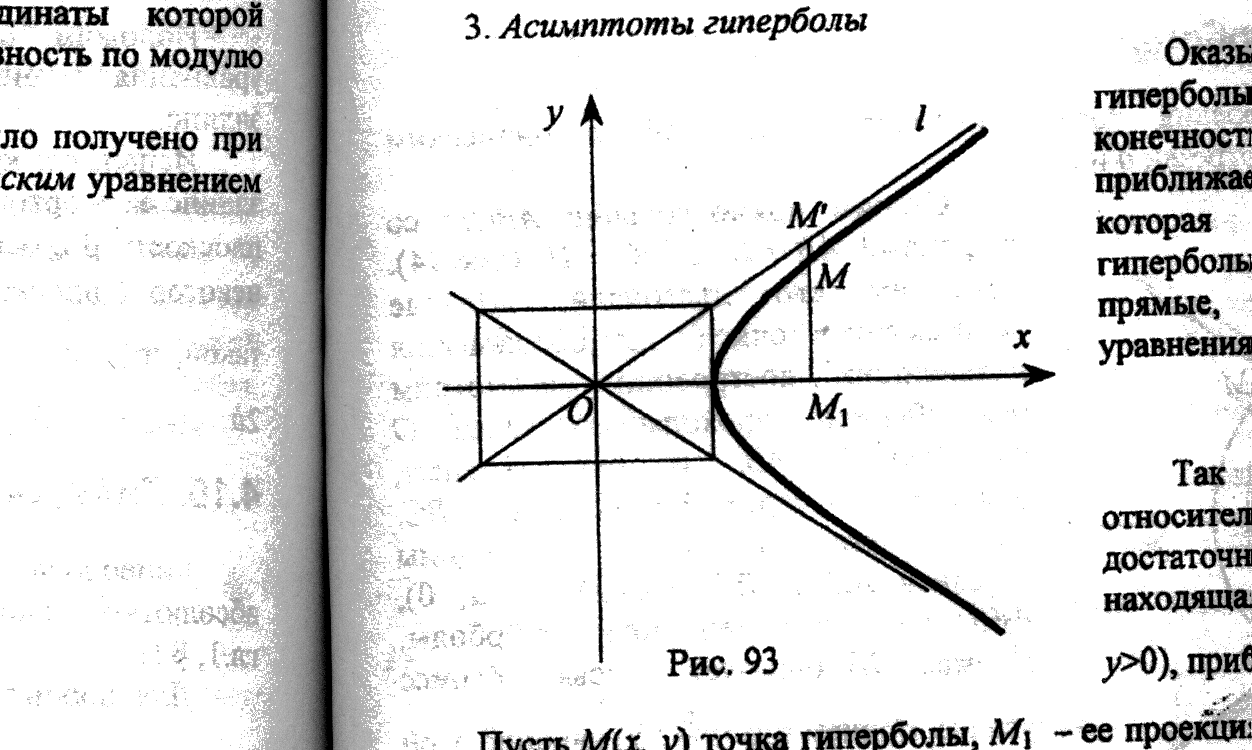
3) Коэф-ты текущ. точки входят в ур-ние G в чёт степенях x2 и y2 => G расположена сим-чно отн-но осей и (0;0). 4) Асимптоты гиперболы: рассмотрим I четв. (x>0, y > 0)
Докажем
для
В
силу симметричности
5)
т.к.
с
> a, то
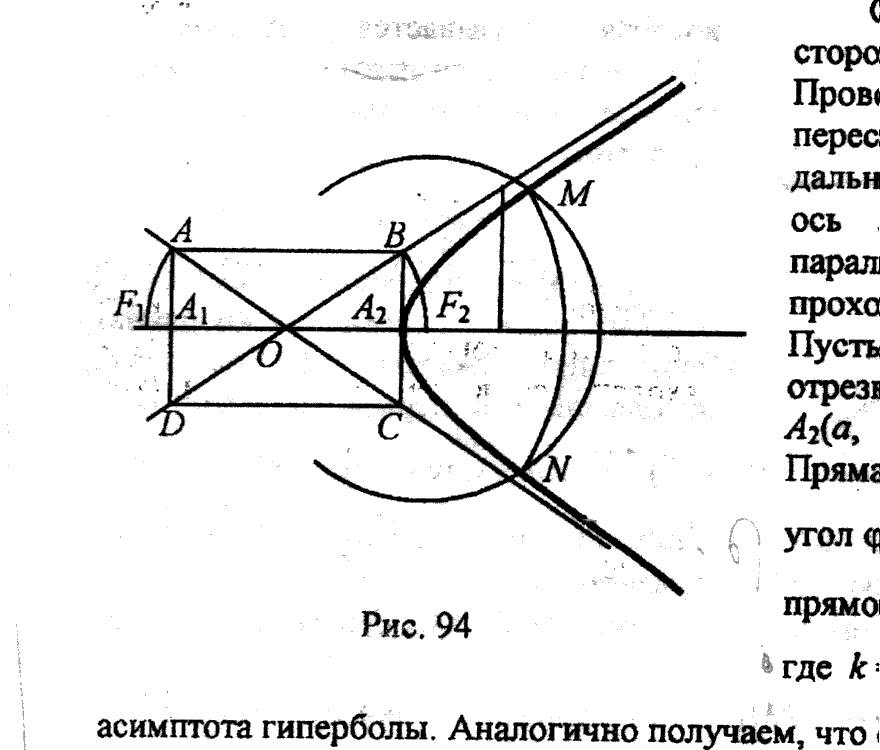
Построение гиперболы Отрезки a и b заданы.
Строим прямоуг-к ABCD: AB=2a, BC =2b AC∩BD=O, OX Э O, OX || AB, OY Э O, OY || BC, !A1 – середина AD, A2 – середина BC => A1(-a;0), A2(a;0) – вершины гип-лы
Где
Аналогично OA - асимптота Найдем фокусы: т.к. c2 - a2 = b2 В ∆A2OB: A2O = a, A2B = b => OB = c. Отложим OF1 = c, OF2 = c => F1 и F2 - фокусы.
(r - произвольный радиус), Т.к. FM1 – FM2 = r – r + 2a = 2a Также FN1 – FN2 = 2a.
пересек-ся в двух точках, если r > c-a |

 зобразим
данные элементы: окр-ть с центром О и
некоторым радиусом r
и точку А. Для проведения кас-ной
построим точку касания на данной
окр-ти. Чтобы найти способ ее построения,
проведём анализ.
зобразим
данные элементы: окр-ть с центром О и
некоторым радиусом r
и точку А. Для проведения кас-ной
построим точку касания на данной
окр-ти. Чтобы найти способ ее построения,
проведём анализ. остроить
прямую, || стороне данного ∆-ка так,
чтобы она разбивала данный ∆ на две
равновеликие части.
остроить
прямую, || стороне данного ∆-ка так,
чтобы она разбивала данный ∆ на две
равновеликие части. .
∆AFB (A=90o,
AF=AB=c)
.
∆AFB (A=90o,
AF=AB=c)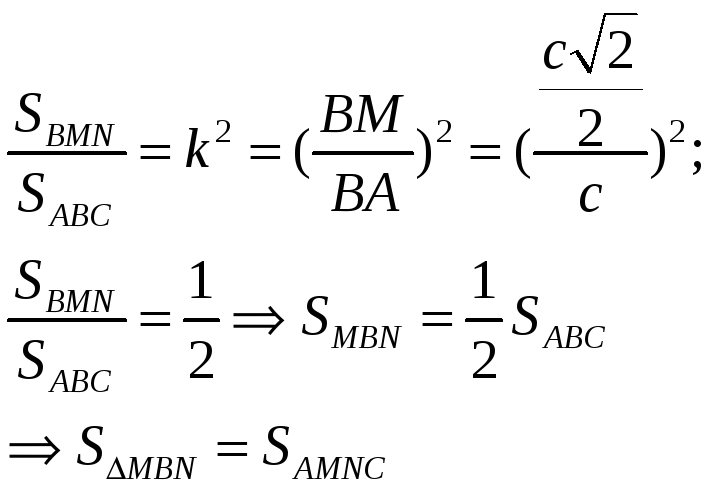
 .
Удвоение куба. Построить
ребро куба, V
которого в 2 раза больше V
данного куба.
.
Удвоение куба. Построить
ребро куба, V
которого в 2 раза больше V
данного куба.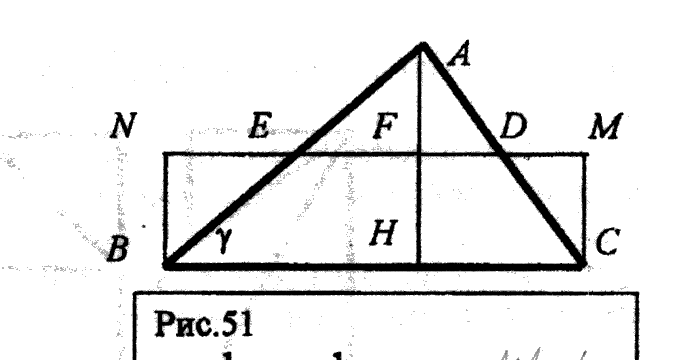 ано:
∆ABC,
BC
= a,
высота
AH
= h,
углы B
и C
- острые.
ано:
∆ABC,
BC
= a,
высота
AH
= h,
углы B
и C
- острые.
 .к.
F1F2=2с,
то
F1(-c;0),
F2(c;0),
.к.
F1F2=2с,
то
F1(-c;0),
F2(c;0),