ГОС математика / Алгебра / GOSy_Algebra_1

3. Алгебраическая операция. Алгебры. Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Изоморфизм групп. Сложение и умножение натур. чисел, сложение арифмет и геометр векторов, сложение и умножение квадратных матриц явл. примерами так .назыв-ых. бинарных операций. Опр. Бинарной операцией на непустом мн-ве А наз. сопоставление всякой упорядоченной паре элементов (а,b), взятых из множества А, некот-ого. однозначно опред-го этой парой элемента с А. при этом пишутДругими словами, бинарная операция • на мн-ве А - это отоб-е. Пр-р: Бин. операция слож-я натур. чисел + явл. отобр-м, при кот., например, упорядоченной паре натур. чисел (2,3) ставится в соответствие однозначно определенное этой паре число 5, то есть. при этом пишут 2+3=5. На мн-ве нату-х чисел вычитание не явл. бинарной операцией, т.к. например для (2,3), при вычитании ставится в соот-вие -1N. В этом случае говорят, что мн-во N не замкнуто относительно вычитания, в то время как, напр-р мн-во четных целых чисел 2Z={2n|n Z} замкнуто отн-но вычитания: для любых а,b 2Z, а-b 2Z. Опр. Бинарная операция, определеная на мн-ве А, наз. ассоциативной, если для люб. а,b,сA , и наз коммутативной, если для любых а,b А . Алгебра-множество, с заданными на нем бинарными операциями.G={А,f1,f2,…}, где А-мн-во, f1,f2,…-алгебраич операции Пр-р агл:{N,+,*}, {Z,+,*} 1 Группы. Рассмотрим операцию сложения на мн-ве Z. Св-ва(+): 1.ассоциативна и коммутативна, 2 сущ-ет особый эл-т 0 такой, что а+0=а для любого а Z, и для всякого целого числа а из Z сущ-ет противоположное число -а Z такое, что а+(-а)=0. (Те же свойства можно отметить и для сложения матриц. Роль нуля выполняет нулевая матрица, а для получения противоположной матрицы достаточно заменить элементы матрицы на противоположные). Св-ва(*): Рассмотрим умножение на мн-ве Q* рациональных чисел, отличных от нуля. Эта операция также ассоциативна и коммутативна, суш-ет особый элемент 1 (аналог нуля) такой, что а*1=а для любого а Q*, и для всякого а Q* сущ-ет обратный элемент а^-1 Q* (аналог противоположного) такой, что а*а^-1=1. (умножение на множестве обратимых матриц также ассоциативно, но не коммутативно, роль единицы играет единичная матрица Те же свойства можно отметить и для умножения подстановок). Опр. Группой называется непустое множество G, на котором определена бинарная операция °, обладающая след. св-ми: 1) операция ° ассоциативна, т.е. для любых а,b,с G 2) существует нейтральный элемент е G такой, что для любого а G 3) Для всякого элемента а G существует симметричный элемент а' из G такой, что . Группа G наз. коммутативной, если групповая операция коммутативна°, т.е. для любых а, b. G . Опр: Порядком группы G назыв исло элементов основеого мн-ва. Обычно групповая операция обозначается либо + и назыв.сложением, либо * и назыв умножением. Пр-ры: 1. бесконечные числовые группы. <Z.+>; <Q,+>; <R,+>; <Q\{0},*>; <R\{0},*>. 2. Конечные группы.<1,*>;<(1,-1),*>; <^nl,*>. 3. Группа обратимых матриц. Основные свойства групп. 1) Eдиница е группы G единственна. Док-во:Пусть el - также единица группы G. Тогда, с одной стороны, e*el=el. так же как е - единица группы, а с другой- e*el=e, так как el -единица в G. Следовательно el=e. 2) Для всякого элемента а группы G обратный элемента^-1 единственный. Док-во: Пусть b также явл. обр. для а, т.е. a*b=b*a=e. Тогда пользуясь ассоциативностью, получаем b=b*e=b*(a*a^-1)= (b*a)*a^-1,=e*a^-1=а^-1. 3) Для любых элементов а и b группы G уравнения а*х=b и у*а=b однозначно разрешимы. 4) Для любого элемента а группы G,(a^-1)^-1=a. 5) Для любых а,b G (a*b)^-1=b^-1* a^-1. 2. Подгруппа. Опр. Подмножество Н группы G наз. подгруппой, если это подмножество само является группой относительно той же операции, рассматриваемой на множестве Н. Из этого определения следует, что для проверки, явл. подгруппой группы G, нужно убедиться в след.: 1) Н замкнуто относительно групповой операции, т.е. если а,b G, то a*b H; 2) Единица е Н; 3) а Н следов, а^-1 Н. Теорема: Непустое подмножество Н группы G яв-ся подгруппой1. а,b G=> a*b H , 2. а Н=> симметр. а^*Н. #1.(=> по определению группы и подгруппы. 2.(<=) А) ассоц-ть на Н выпол-ся в виду того,что операция * ассоц-на для всех эл-тов из G в частности для эл-тов из НG. Б) нейтр.эл.еН. ! а Н, тогда по 2 усл.признака а^*Н, тогда по 1 усл.признака а^**а Н и а* а^*Н , значит еН. Н-группа=> # Теорема: пересечение двух подгрупп является подгруппой. 3. Изоморфизм(Лат. «одинаковость») Опр. Группы G и G' наз. изоморфными, если м/у ними можно установить взаимно однозначное соответствие, при кот. для любых эл-тов а,b G и соответствующих им эл-тов а',b' G' произведению а*b соответствует произведение а'*b' Более подробно:1.Образы различных элем. различны.2.гр. изоморфны, если существ изоморфизм одной из них на другую. IIP-P: 1. Аддитивные группы целых чисел и четных чисел изоморфны между собой.(в соответствие всякому целому числу к четное 2к) 2. Все бесконечные циклические группы изоморфны между собой; изоморфны между собой также все конечные циклические группы данного порядка n. (Группа G называется циклической гр, если она состоит из степеней одного из своих элементов а, т.е. совпадает с одной из своих циклических подгрупп {а}; элемент а называется в этом случае образующим элементом гр G) (Для всякого простого числа р существует единственная, с точностью до изоморфизма, конечная группа порядка р.) ОПР: Отображ-е φ: G на G’наз-ся гомоморфизмом, если оно сохран-т операцию м\у соотв-щими при φ эл-ми, т.е.выпол-ся рав-во: φ(ху)=φ(х)φ(у). Гомоморфизм опред-ся ч\з понятие отображения (отобр-е: кажд.эл-т из Х имеет едиств.образ в У), а изоморфизм-взаимнооднозн.отображение.	4.Кольца, поля. Примеры. Простейшие свойства. Подкольцо, подполе. Кольцом наз.мн-во элементов К, на кот-ом определены операции сложении и умножения, причем выполнены след условия: 1) «+» коммут (а+b)+с=а+(b+c) и ассоц а+в=в+а для любых а,b,с К. 2)Суш-ет эл-т 0 К такой, что 0+а=а+0=а. 3)для люб. а К сущ-ет эл-т -а К такой, что а+(-а)=0 . 4) «*» ассоц:(а*b)*с=а*(b*с) для любых а,b,c К. 5) «*» дистриб относительно сложен а*(b+с)= а*b+а*с для любых а,b,c К. Если «*»в кольце коммун, то кольцо- коммун-ое. Кольцо К-кольцо с единицей,если сущ элемент е К такой, что для любого а К Пример: Z,Q,R-ассоц кольца(К-числовое множ-во явл-cя кольцом a,bK =>) Св-ва: 1)(св-во нуля)Для эл-та а К: а*0=0*а Док-во: а*0=а(0+0)=а*0+а*0 => а*0=а*0+а*0 прибавим к обеим частям -(а*0), получ 0=а*0 Так же док-ся, что 0*а=0 2)(правила знаков)Для эл-ов а и b К (-а)b=а(-b)=-(аb), (-а)(-b)=(аb) Док-во: Имеем ab+(-a)b=(a+(-a))b=0b=j=0 (-a)b=-(ab); аналог-но док-ся, что a(-b)=-(ab). Используя доказ-ое, получ.:(-a)(-b)=-(a(-b))=-(-(ab))=ab. Вычитанием в кольце К наз бин. операция- : а-b+а+(-b) для любых а,b К 3)Умнож в кольце дистриб относ-но вычитания :(а-b)с=ас-bс. Док-во: используя опр «-», дистриб «*»относ «+» и св-ом 2:(а-b)с=(а+(-b))с=ас+(-b)с=ас+(-(b))=ас-bс. Опр:! К=<К, +,*>-Кольцо Н=<Н, +,*>.Н- подкольцо кольца К, если 1)НК, а-bH, a, bH(подгруппа аддитивной группы кольца К)2) люб. a,b из Н: a*b из Н Признак подкольца: Подмн-во Н кольца К явл подкольцом 1. Н замкнуто относ слож-я и умн-я . 2.0 Опр. Поле-это коммут кольцо с единицей и для каждого ненулевого эл-та сущ-ет обратный эл-т. Пример: поле комплексных чисел (или Полем назыв множ-во элем-ов Р, на котором определена операция «+» и «*», причем выполняются следущие условия(аск. поля: 1. «+» коммут и ассоц: (а+b)+с=а+(b+c) , а+в=в+а для любых а,b,с Р.2)Суш-ет эл-т 0 Р, назыв нулем, такой, что 0+а=а+0=а. 3)для любого а Р сущ-ет эл-т -а Р такой, что а+(-а)=0 .4) «*» коммут и ассоц: a*b=b*a и (а*b)*с=а*(b*с) для любых а,b,c К. 5)существ элем 1 Р, назыв единицей:1 не 0 и 1*a=a , a Р 6)Люб. а Р, а не 0, сущ элем а^-1 Р, назыв обратным к а:а*а^-1=1 7) «*» дистриб относительно сложен а*(b+с)= а*b+а*с для любых а,b,c К.Примеры:R-поле действ чисел, Q- поле рацион чис. Опр: Подполем F поля Р назыв подкольцо поля Р, в котор каждый ненулевой элем обратим.(Элем а кольца К обратим, если сущ b из К:a*b=b*a=1k, где элем а, b взаимно обратны) Признак подполя:F Р является подполем поля Р выполняются условия:1)Люб.a,b из F a+b из F, a*b из F;2) Люб.a из F сущ (-а)из F :a+(-a)=0=(-a)+a;3) ) Люб.a из F а не 0 сущ а^-1 F: а+ а^-1=1= а^-1*а Пример:Q- подполе поля R)) Свойства(специф св-ва полей). 1)Для эл-ов а и в поля Р, если аb=0, то а=0 или b=0. Док-во: если а=0, то док-ть нечего. Пусть a не 0, тогда сущ а^-1 Р. Умножим аb=0 на а^-1, получим а^-1(ав)= а^-10=0=> ( а^-1 а)b=1*b=0=>b=0. Cлед-е:В поле нет делителей нуля, т.е.если а не 0 и b не 0 , то аb не 0. 2)(св-во сократимости)Если ас=bс и с0, то а=b. Док-во: ас=bс => ас-bс=0=> (а-b)с=0, а т.к. по условию с0 и в поле нет делителей нуля, а-b=0 => а=b. Опр:Для любых ял-ов а и b0 поля Р произведение аb^-1 наз отношением этих эл-ов(дробью)и записывается в виде(а-числитель, b-знаменатель,b не 0). Сопост-ние всякой упоряд-ой паре элементов(a,b)элем ab^-1 назыв делением и пишут:a:b=ab^-1 3)Для любых отношений и поля Р 1) = =>ad=cb;2)+\- =;3) *=; 4)если не 0, то ()^-1=5)(осн св-во дроби) =.#1) = <=> ab^-1= сd^-1 ab^-1*bd= сd^-1*bdad=cb;2)+\- = ab^-1+\-сd^-1=(ad+\-bc)b^-1d^-1=(ad+\-bc)( bd)^–1=; Поля из одного элемента не существует	5. СЛУ. Равносильные СЛУ и элем-ые преобр-ния сис-м. Различные способы реш-ия сис-м. Опр. Линейным ур-ем с n неизвестными наз ур-ние вида , где - неизв-ые, - коэф-ты,b своб.член. Опр: СЛУ наз-ся всякая упорядоченная совокупность m линейных ур-ний с n переменными: Такую систему удобнее записывать в матричной форме. Опр. решением СЛУ с n неиз-ыми наз такой набор из n чисел, что каждое ур-ние системы обращается в верное числовое рав-во при подстановке этого набора чисел соотв-но вместо неизвестных . Опр. СЛУ наз-ся совместной, если она имеет решения и несовместной, если решений нет. Пример несовместной СЛУ: Опр. Совместная СЛУ наз-ся определённой, если она имеет единственное решение и неопределённой, если она имеет более одного решения, при этом каждое ее решение наз частным реш сист-мы, совокупность всех част реш сис-мы наз общее решение сис-мы. Опр. Решить с-му это значит выяс-ть, совместна она или несовместна. Если совм найти ее общ реш. Опр. две сис-мы эквивалентны (равнос-ны), если они имеют одно и тоже общее реш, т.е. если каждое реш одной сис-мы яв-ся реш другой,и наоборот. Эквив-ные сис-мы получаются, в частности, при элем преобр-ниях сис-мы при условии, что преобразование выполняется лишь над строками матрицы. Опр. СЛУ наз однородной, если все свобные чл=0. Замеч: Однородная система всегда совместна, т.к. х1=х2=…=хn=0 явл реш сис-мы, его наз нулевым (тривиальным )реш-м. Опр. Матрицей наз-ся любая прямоугольная таблица чисел. Опр. Матрицей СЛУ наз-ся матрица из коэф-ов при переменных. Опр. Расширен. матрицей системы наз-ся матрица А, если к ней приписать столбец свободных членов. Элементарные преобразования СЛУ: 1.Перемена мест ур-ий системы. 2.Умножение уравнения на число отличное от 0. 3.(главное)Умножение ур-я на число и прибав-е к др. ур-ю. 4. Добавление или отбрасывание нулевого ур-я. Элементарные преобразования матриц: 1.Перемена мест строк матрицы. 2.Умножение строк на число отличное от 0. 3.(главное)Умн-ние строк на число и прибав-е к др. строке 4.Добавление или отбрасывание нулевой строки.Лемма: При элементар. преобр-х СЛУ получается система эквивал. первоначальной. Опр. Рангом матрицы наз-ся её строчный ранг. (Матрицу А, с помощью эл-ых преобр-й, приводят к ступенчатому виду без нулев. строк, тогда ранг матрицы А =числу оставшихся строк) Тh: Для того чтобы сис-ма од ур-ний имела не нулевые реш необх и дост, чтобы ранг ее осн матрицы был меньше числа неизв. Критерий совместности СЛУ: Th(Кронейкера-Копелли): (эта th дает ответ на ? о совместимости системы)! Дана СЛУ с m уравнениями и с n неиз-ми.СЛУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Решение СЛУ 3 методами: 1.Метод Гауса: 1) Запишем расшир.матрицу системы. Путём элемен-ых преобр-й строк матрицы приводим её к ступенчатому виду. Если в рез-те элемент-ых преобр-й появится строка вида 0 0 … 0 | , то этой строке будет соответствовать ур-е: , кот-е не имеет реш., а значит не имеет решение и вся система (*), т.е (*)-несовместна. 2.1) Если в рез-те элем-ых преобр. матрица А будет преобразована в треугол. матрицу, то проводя элем. преобр. снизу вверх мы получим единичную матрицу: , кот-й соотв-т следующая СЛУ:, а значит (*) имеет единств. решение (), т.е система совместна и определена. 2.2) Если в рез-те элем-ых преобр-й мы получили ступенчатую матрицу, то меняя столбцы местами(вместе с переменными) приведём к следующему виду(), где Т – треугольная матрица, Р –прямоугольная , - столбец свободных членов, мы получим следующую систему: Преобразуем матрицу Т с помощью элемен-ых преобр-й к единичной матрице (единичному виду), тогда получим следующую систему: Выразим x1из первого ур-я, x2- из второго и т.д и получим систему: Перемен. наз-ся глаными, а … - свободными. Придадим различ. знач. свободн. перем. и будем находить значения главных пер-ых, т.е система (*) будет иметь бесконечное мн-во решений, т.е будет совместной и неопределённой. Пример: 1)Ответ: Система определена (единственное решение), т.к все уравнения различны. 2) -данная система имеет бесконечно много решений, т.к имеет одинаковые строчки. 3) - данная система не имеет решения т.к 46. 4) (на метод Гауса) получимГлавные переменные: Свободные: 2.Формулы Крамера Опр. Пусть дана квадратная матрица А порядка n. Минором элемента aij наз-ся определитель матрицы полученной из данной путём вычёркивания i-ой строки и j-того столбца. Опр. Алгебраическим дополнением элемента aij наз-ся минор этого элемента, умноженный на (-1)^i^+^j. Запишем СЛУ в виде матричного ур-я, где А–матрица системы, Х–столбец переменных, а В-столбец свободных членов:A . Домножим обе части ур-я слева на А^*: А^*A . По теореме(Если А- квадратная матрица, а А^* - присоеденённая к ней матрица, то ) получим: (|А1|– это определитель матрица А, если в А первый столбец заменить столбцом свободных членов. |А2|– это определитель матрицы А, если второй её столбец заменить столбцом свободных членов,…, |Аn|– это определитель матрицы А, если её n-ый столбец заменить на столбец свободных членов.). Умножим А*В и получим следовательно Х = . Упростив получим …………….. Тогда, 1)если |А|, то решение системы находится по формулам Крамера: 2), но хотя бы один из определителей не равен нулю, то СЛУ не совместна. 3) и , то СЛУ либо совместна и неопределенна, либо несовместна. 3.Матричный способ решения СЛУ: Опр. Транспонированием матрица А наз-ся такое её преобразование, когда каждая строка матрицы А становится столбцом того же номера. Обозначение А^-1. Опр. Пусть дана квадратная матрица А порядка n, матрица В наз-ся обратной для матрицы А, если . Обозначается:В=А^-1. О матрице А говорят что она обратима. Правило нахождения обратной матрицы: Запишем квад-ую матрицу А, а справа к ней припишем единичную(А|Е). С помощью элемен. преобр. приведём матрицу к ступенч. виду Если слева от черты окажется нулевая строка, то матрица А не имеет обратной. если Нулевой строки нет, то поднимаясь снизу вверх получим слева единичную матрицу, а справа матрицу обратную А. Матричный способ решения СЛУ: Запишем матрицу коэффициентов Получим ур-е: . Если матрица А- обратима, т.е её ранг =n, то существует обратная матрица А^-1 и умножим слева на обратную матрицу, тогда получится, по ассоциативному закону, а , следовательно .
6. Функция Эйлера. Классы срав-ых чисел, взаимно простых с модулем. Приведенная сис-ма вычетов. Тh Эйлера и Ферма. Опр. 2 целых числа а и b наз-ся сравнимыми по модулю m, если они дают одинаковые остатки при делении на m. Опр. 2 целых числа а и b наз-ся сравнимыми по модулю m, если существует t принадлежащий Z, что a=b+mt. Опр. пусть m из N,m>1.a,b из Z наз-ся сравнимыми по модулю m если их разность делится на m. Обоз-ся a≡b(mod m). Опр. Если (a,m)=d, то и все числа класса имеет с m тот же самый НОД.Класс чисел наз-ся взаимно простым с mod m, если (a,m)=1. Опр. Полной системой вычетов по mod m наз совокупность чисел, взятых по одному из каждого класса вычетов по mod m. Опр. модулем, наз классы, у к-ых НОД=1. Опр. Приведенной сис-ой вычетов по модулю m наз-ся совокупность вычетов, взятых по одному из каждого класса, взаимно простого с mod. Пример: 1,29,-5,71-привед сис-ма вычетов по mod 12, т.к. из 12 классов по этому mod имеется 4 класса чисел,взаимно простых с mod, то оставшиеся числа образуют привед сис-му вычетов. Th: если в полной системе вычетов отбросить представителей всех классов, не взаимно простых с mod, то оставшиеся числа образуют привед сис-му вычетов. Д-во: в полной сис-ме вычетов имеются представители всех классов,в том числе по одному представителю классов,взаимно простых с mod. Все остальные числа полной сис-мы вычетов по усл отбрасываются, т.е. остается привед сис-ма вычетов. Опр. ! . Обозначим,ч/з -кол-во натур чисел, не превосходящих n и взаимно простых с n. задает ф-ию на множестве нат чисел, ее наз ф-ей Эйлера. Опр. ф-ей Эйлера наз число классов по mod n взаимно простых с этим mod. Def: ф-ей Эйлера наз число нат чисел, не превосходящих n и взаимно простых с n. Пример: по mod 1 имеется один класс чисел, взаимно простых с mod, поэтому . По mod 12 имеется 4 класса чисел, взаимно простых с mod 12, т.е. . Th: (признак пр сис-мы вычетов) Всякая совокупность чисел, попарно не сравнимых по mod m и взаимно простых с модулем, есть Привед сис-ма вычетов. Док-во: т.к. числа попарно не сравнимы, то они взяты из разных классов, т.к. они взаимно просты с mod, то они взяты из классов взаимно простых с mod, т.к. их , т.е. каждого класса взаимно простого с mod, взятого по одному представителю. Th: если (a,m)=1 и х пробегает привед сиc-му вычетов, то ax тоже пробегает прив сис-му вычетов по mod m. Док-во: 1)пусть – прив сис-ма вычетов по mod m, тогда – Тоже штук. 2)эти числа попарно не сравнимы по mod m , Т.к. (a,m)=1, то – противоречие. 3)т.к. (a,m)=1 , , то .Все три пункта теоремы выполнены. Чтд. Опр. Функция , определенная на мн-ве нат чисел, наз-ся мультипликативной, если для . Функция , определенная на мн-ве нат чисел наз-ся вполне мультипликативной, если рав-во (1) выпол-ся для любых нат чисел a и b Св-ва ф-ции Эйлера: 1)ф-ия Эйлера мультипликативная, т.е. , при (a,b)=1 Док-во: 1 2 3 4 … b b+1 b+2 b+3 b+4 … 2b 2b+1 2b+2 2b+3 2b+4 … 3b (a-1)b+1 (a-1)b+2 ….. (a-1)b+b=ab 1-ая строка-Пол сис-ма вычетов по mod b, чисел взаимно постых с b. ! (r,b)=1, тогда r-ый столбец состоит из чисел xb+r по Лемме: (xb+r,b)=(b,r)=1, т.е. весть r-тый столбец состоит из чисел взаимно простых с b. Мы имеем столбцов чисел взаимно простых с b. Числа вида xb+r, где x=0,1, …, a-1 составляют полную систему вычетов по mod a по теореме о ПСВ (любая совокупность m чисел, попарно не сравнимых по модулю m есть полная сис-ма вычетов). Среди них чисел взаимно простых с a. столбцов чисел взаимно простых с b. чисел взаимно простых и с a, и с b, т.е. . 2), p-простое число. Это свойство следует из определения функции Эйлера. 3) 4)Если - каноническое разложение числа , то док-во:1), 2) числа не взаимно простые с . Среди чисел кратных p будет . Взаимно простых с p и следовательно с . Из мультипликативности следует утверждение теоремы, т.к. . Чтд. Пример: Th Эйлера: если (a,m)=1,, то . Док-во: ! -некоторая привед сис-ма вычетов по mod m. По теореме о привед сис-ме вычетов: также образуют привед сис-му вычетов. Установим взаимно однозначное соответствие м/у 2 сис-ми, сопоставив каждому из чисел сравнимое с ним число из сис-мы так что , перемножим эти сравнения: разделим на получаем: чтд Th Ферма: если p-простое, и a не кратно p,то . Доказательство этой теоремы следует из теоремы Эйлера, так как . Пример: Найти 2 последние цифры от числа 1997^1963.r т.е остаток будет 73.	7.Век-ное пр-во, подпр-во.прим и прост.св-ва в.прос-в линейная зависимость и независимость (ЛЗ/ЛНЗ) с-мы в-ов. Начнем с опр геом.в-ра. Геом.век-р-напр.от-ок(от-ок с упорядоч концами).лин.опер над ними: сложение, вычитание,умножение на число. ОПР ариф.n-мерным вектор-это сов-сть n чисел, в общем случае, под век-ом понимают упоряд. св-сть любых эл-тов какого-либо поля., опер-ии те же самые. Опр. Пусть дано поле Р, элементы которого будем называть скалярами, и дано непустое мн-во V, эл-ты которого будем называть векторами и обозначать Мн-во V наз-ся векторным пр-ом над полем Р, если на V определена бинарная операция сложения векторов, и операция умножения вектора на скаляр, (т.е. ) и выполнены следующие аксиомы (аксиомы вект.пр-ва): 1) коммутативная группа, то есть: а) сложение векторов коммутативно и ассоциативно ; б)эл-т, наз. нулевым вектором:; в)вектор,наз.пр-ым для:. 2) Умножение вектора на скаляр ассоц-но: дляи скаляровимеет место рав-во. 3) Выполняются два дистр. закона: для и 4) Св-во умножения на единицу 1 поля Р:для. Обратим внимание на то, что нулевой вектор обозначается, а нулевой и единичный элементы поля Р- через 0 и 1. Пр-ры: П1: V=R^n над P=R;П2: V=C над P=R(обратно нет);П3: V=R над P=Q(обратно нет);П4: V- мн-во всех непр.ф-ций действ. переменного, заданного на фиксир. отрезке над P=R;П5: V-все мн-ны P[x] над P=R;П6: V-матрицы одинарного размера над P=R и т.д..2) 1)Арифметическое n-мерное векторное пр-во.2) Пространство мн-ов P[x] над полем P;3) Мн-во мн-ов, степень к-ых ,т.е. 4) Мн-во матриц одного размера с действительными коэффициентами над R.5) Мн-во R чисел над полем Q чисел.6) Мн-во R чисел над полем R чисел.7) Q не является векторным пр-ом над полем R. Сущ.и ед-ость: 1.,для:.Существование нулевого эл-та очевидно из опр. вект.пр-ва. Док-м единственность: если и-два нулевых эл-та, то += и +=+=,откуда =. 2.вектор, называемый противоположным для, такой, что . Существование против. эл-та очевидно из опр. вект.пр-ва. Док-м единственность: если и-два противоположных эл-та для , то +[a+]= += и [+a]+ = += , откуда =. Св-ва: 1. Для любого вектора а и любого натурального n имеем . #из акс-ом 4 и 3 и опр.: # 2. Для иимеем:. # # 3.Дляиимеем:. #аналогично предыдущему # 4. или. #Если ,то док-ть нечего. Пусть ,тогда в поле Р обратный эл-т,и мы получаем: достаточность очевидна, т.к. следует из 2 и 3 св-тв.# 5.Дляиимеем: #; # 6.Определим вычитание векторов формулой для.Тогда умножение на скаляр дистрибутивно относительно вычитания векторов:. ## (по другому: из выше изложенного выводится сущест-е и един-ть разности a-b, т.е. такого эл-та, который удовлетворяет уравнению. Действительно, можно положить a-b=a+(-b), т.к.b+[a+(-b)]= =[b+(b)]+a=0+a=a.Если же сущ-ет еще такой эл-т с, который удов-ет урав-ю,т.е. b+c=a, то прибавляя к обеим частям этого рав-ва эл-т –b, получаем, что c=a+(-b)) Опр. Пусть даны (геом или арифмет n-мерные)и даны действ числа . Тогда в-р на-ся лин.комбин дан.в-ов.Так же лин выраж-ся ч/з . Опр.Пусть дано векторное пространство V над полем Р.Непуст подмн-во HV называется подпространством над полем Р, если оно само является пр-ом относительно тех же операций над векторами. Пример: в 3-мерном ариф.век-ом прост-ве подпр-ми будут: -мн-во всех век-в, у кот 2-я и 3-я компоненты=0;-мн-во всех век-ов, у кот 3-я компонента=0;-мн-во, сост-щее из одного нул.в-ра =(0,0,0) Опр.Система векторов называется ЛЗ, если сущ-ют числа , среди которых есть отличные от нуля, такие, что . При этом рав-во наз-ся линейной зависимостью данных векторов. Пр-ры: =(1,2,3),=(2,3,4),=(3,4,5): = + + - =0. . Св-ва: 1. Конечная сис-ма век-ов, содер-ая нул. вектор, ЛЗ. 2. Если конечная сис-ма векторов содержит ЛЗ подсис-му, то она сама ЛЗ. 3. Конечная сис-ма век-ов, сод-щая более одного век-ра, ЛЗ, когда она сод-ит век-р, явл-ся лин комб-ей остальных век-в сис-мы. Опр. Система векторов называется ЛНЗ, если она не яв-ся ЛЗ, т.е все коэфф-ты линейной комбинации равны нулю. Бесконечная система векторов ЛНЗ, если любая ее конечная подсистема ЛНЗ. Пр-ры: e1=(1,0,0),e2=(0,1,0) , e3=(0,0,1): (1,2,3)=(0,0,0) Т-ма(осн т-ма о ЛЗ)если сис-ма век-ов лин выр-ся ч/з с-му в-ов и , то с-ма в-ов ЛЗ. (образно говоря, если «длинная» с-ма в-ов лин выр-ся ч/з «короткую», то «дл-ая»с-ма в-ов ЛЗ) Док-во:нужно док-ть чисел ,среди к-рых есть отличные от нуля,таких,что = Др сл-ми, нужно док-ть ненул.реш-ия вект-го ур-ния = По усл-ю,с-ма в-ов лин выр-ся ч/з с-му := =,..,=, для нек-рых чисел ,i=1,..,k, j=1,..,m. След-но, +..+.Раск-ем скобки и сгруппир-ем по в-ам :++… +=.Это рав-во будет вып-но,если каж-ый из коэф-нтов окажется равным нулю. Приравняв кад-ый коэф-нт к нулю,получим однородную с-му лин.ур-ий(т.е.в кот-ой все ее своб члены=0) По усл-ю, k > m, число ур-ний < числа переме-ных(сис-ма лин ур-ий вытянута по гориз-ли).По теор-ме(если в однор с-ме лин ур-ий число ур-ий < числа перем-ых,то она имеет ненулевое реш-е),эта с-ма имеет ненул р-ние . Но тогда =Это док-ет ЛЗ с-мы в-ов След-е 1: Если с-ма в-ов ЛНЗ и лин выр-ся ч/з с-му {,то. След-е 2:В n-мерном в-ом прост-ве конеч с-ма в-ов,сод-щая более n в-ов, ЛЗ. След-е 3: В n-мерном в-ом прост-ве ЛНЗ с-ма в-ов,сод-щая более,чем n в-ов. Теорема: если с-ма в-ов ЛНЗ и выр-ся ч/з др сис-му, то первая сис-ма короче второй.	9. Простые числа. Беск-сть мно-ва простых чисел. Каноническое разл-ние сост-го числа и его единс-ть. Опр. Нат-ое число р наз-ся простым, если p>1 и оно имеет ровно два делителя 1 и р. Опр. Нат-ое число n>1 наз-ся составным, если n имеет более двух делителей. Множество Свойства простых чисел: 1. Для любого натурального числа n>1 наименьший делитель, отличный от единицы, есть число простое. Д-во: Пусть p – наименьший натуральный делитель n, отличный от 1 (n имеет натуральный делитель, отличный от от 1, например, n). Очевидно, что p – простое число. Иначе оно имело бы такой делитель a, что 1<a<p, но а, будучи делителем p, было бы и делителем n, что противоречит выбору числа p. 2. Если p, q – простые числа и pq, то p=q. 3. Для простого, либо , либо (a, p)=1. Д-во. Так как число p имеет только 2 натуральных делителя: p и 1, то (a, p) =p или (a, p)=1. В первом случае , во втором – a и p – взаимно простые числа. 4.Если . Д-во. Пусть . Если a не делится на p, то (a, p)=1. Тогда по св-ву взаимно простых чисел . Теорема (Евклида). Мн-во простых чисел бес-но. Док-во: допустим противное, что мн-во простых чисел конечно и выпишем их все: . Составим новое число . Это число не может быть простым, т.к. оно > простого числа, значит оно составное, а значит, у него есть делитель q, т.е. . Значит q совпадает с одним из p. Пусть Пришли к противоречию, значит наше предположение не верно. Основная теорема арифметики. Всякое нат-ое число >1, яв-ся либо простым, либо разлагается в произв-ие простых множ-ей, причем однозначно с точностью до порядка их следования. Док-во: докажем возм-сть методом полной индукции n=2, где 2 – простое. Предп-им, что любое число < n, представимо в виде произв-я простых чисел, либо простое. Рассм-им число n. Если n – простое, то теорема док-на. Если n – составное, то значит, у него есть делитель a, n=ab, причем 1<a<n, 1<b<n. Значит для a и для b выполняется индуктивное предпол-е, т.е. они разлагаются в произведение простых чисел: Но тогда и n разлагается в произведение простых чисел: . Док-ем ед-сть методом мат.индукции. Пусть n=2. Предп-им, что все числа <n однозначно представимы в виде произ-ия простых чисел. И док-ем, что n тоже представимо однозначно. Д-ть будем методом от противного. Пусть неоднозначно. Тогда .Произ-ие стоящее в правой части и произв-е стоящее в левой части . Тогда по 4-ому св-ву простых чисел, один из мн-лей , пусть . Тогда по 2-ому св-ву простых чисел . Тогд . Для имеет место индуктивное предположение, т.е. Теорема доказана. Разлагая натур.число на простые мн-ли мы видим, что простое число может встречаться не один раз, а раз. 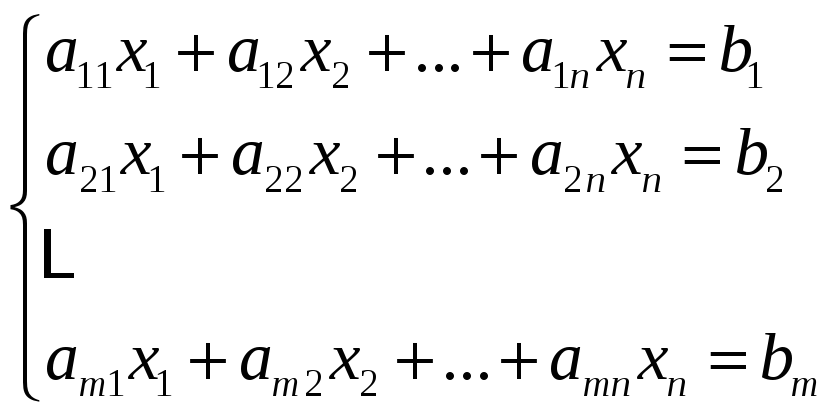Тогда число n записывается в виде Опр.Каноническим разложением нат-го числа n наз-тся представление n в виде ,где-попарно-различные простые числа, -натуральные числа. С помощью канон-го разложения можно находить НОД и НОК чисел. Дополним каждое из них со множителями которые имеются в одном, но отсутствуют в другом. и , где - м.б. и нулями.