
- •Вспомогательные сведения
- •Формулировка принципа наименьшего принуждения
- •Доказательство принципа наименьшего принуждения
- •Энергетическая трактовка принципа гаусса
- •Экстремальное свойство реакций связей
- •О геометрической интерпретации принципа гаусса
- •Дифференциальные уравнения движения и принцип гаусса
- •Заключение
- •Литература
Учреждение образования
Брестский госуд. Университет
Имени А. С. Пушкина
Физический факультет
Принцип наименьшего принуждения
(Реферат по курсу «Специализация»)
Выполнил студент 3 курса
Герман Владимир Владимирович
Брест, 2011
Содержание
-
Введение 3
-
Вспомогательные сведения 3
-
Формулировка принципа наименьшего принуждения 5
-
Доказательство принципа наименьшего принуждения 11
-
Энергетическая трактовка принципа Гаусса 12
-
Экстремальное свойство реакций связей 12
-
О геометрической интерпретации принципа Гаусса 12
-
Дифференциальные уравнения движения и принцип Гаусса 14
-
Заключение 15
-
Литература 17
В 1829 году в журнале «Крелле» (Crelle Journal fur die reine Mathematik) был опубликован мемуар Гаусса под названием «Об одном новом общем принципе механики» (Ube rein allgemeines Grundgesetz der Mechanik).
Карл Фридрих Гаусс (1777–1855) – крупнейший математик Германии первой половины XIX века. В его научной работе сочетались исключительно глубокие исследования в области чистой математики (алгебра, теория чисел, теория эллиптических функций, дифференциальная геометрия поверхностей, неевклидова геометрия и т.д.) с не менее глубокими исследованиями в области приложений математики к задачам астрономии, высшей геодезии, теории магнетизма и др. Высокие научные заслуги Гаусса получили всеобщее признание в ученом мире Европы. В частности, Гаусс был член-корреспондентом Петербургской академии наук с 1802 по 1824 год и её иностранным почетным членом с 1824 года.
Упомянутый мемуар Гаусса состоял всего из четырех страниц текста. Это была его единственная работа по общей механике. В ней сформулирован новый принцип механики, который впоследствии стали называть принципом наименьшего принуждения или принципом Гаусса. Гаусс отмечал, что существенно новый принцип механики уже не может быть найден, но всегда интересно и поучительно исследовать законы природы с новой точки зрения, придём ли мы при этом к более простой трактовке того или иного частного вопроса или достигнем большей точности формулировок. Вот такая новая точка зрения и предложена в принципе наименьшего принуждения.
Этот принцип является наиболее общим принципом механики. Вместе с тем он наиболее прост при использовании. Область приложений принципа Гаусса весьма широка. Он применим в задачах механики, динамике сложных управляемых систем, динамике живых организмов, квантовой физике, теории гравитации и т.д.
Из-за общности, красоты, простоты и наглядности принципа наименьшего принуждения его без преувеличения можно назвать жемчужиной теоретической механики. «Насколько я знаю, – писал выдающийся французский математик Ж. Бертран, – не существует ни одной общей теоремы динамики, которая казалась бы более способной вызвать восхищение тонкого ума, но еще мало искушённого в аналитических преобразованиях и породить у него желание изучить науку, которая позволила бы ему ясно воспринять её доказательство».
Вспомогательные сведения
Для формулировки принципа Гаусса следует предварительно дать необходимые определения и понятия из теоретической механики.
Рассмотрим систему материальных точек Pv, v = 1, 2, ..., N, с массами mv, радиусы-векторы и прямоугольные декартовы координаты которых в неподвижной системе координат обозначим через rv и xv, yv, zv, через vv и wv обозначим скорость и ускорение точки Pv. Очень часто при движении системы положения и скорости ее точек не могут быть произвольными. Ограничения, налагаемые на rv и vv, , которые должны выполняться при любых действующих на систему силах, называются связями. Если на систему не наложены связи, то она называется свободной. Системы со связями называют несвободными.
В общем случае связь задается соотношением f(ru ..., rn, Vj, ..., vn, t) > 0. Если в нем реализуется только знак равенства, то связь называется удерживающей. Например, при движении точки P по сфере постоянного или переменного радиуса R с центром в начале координат имеем удерживающую связь x2 + y2 + z2 - R2 = 0.
Если же в соотношении f > 0 реализуются как знак равенства, так и знак строгого неравенства, то связь называется неудерживающей. Пусть, например, две точки Р1 и Р2 связаны нерастяжимой нитью длины l. Здесь имеем неудерживающую связь, задаваемую соотношением l2 – (xJ – x2)2 – (yx – y2)2 – (z1 – z2)2 ≥ 0, которое означает, что точки не могут находиться одна от другой на расстоянии, большем l.
Если соотношение, задающее связь, не содержит проекции скоростей точек системы, то эта связь называется геометрической (или голономной), в противном случае связь называется дифференциальной. Иногда дифференциальную связь можно представить в виде зависимости между координатами точек системы и временем (как в случае геометрической связи). Тогда ее называют интегрируемой. Неинтегрируемую дифференциальную связь называют еще неголономной.
Точки несвободной системы не могут двигаться в пространстве совершенно произвольно. Их кинематически возможные (то есть допускаемые связями) координаты, скорости, ускорения и перемещения должны удовлетворять некоторым соотношениям, вытекающим из уравнений связей.
Помимо
перемещений, соответствующих
действительному
(истинному, реальному) движению, в
механике важны еще так называемые
виртуальные (воображаемые) перемещения.
Виртуальным
перемещением
точки Р, называют такое ее малое
перемещение
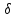 rv
= (
rv
= (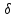 xv,
xv,
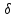 yv,
yv,
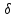 zv),
мысленно осуществляемое из данного
положения при фиксированном времени
t,
которое с точностью до членов первого
порядка малости включительно относительно
zv),
мысленно осуществляемое из данного
положения при фиксированном времени
t,
которое с точностью до членов первого
порядка малости включительно относительно
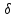 xv,
xv,
 yv,
yv,
 zv
не нарушает связей.
zv
не нарушает связей.
Поясним
это на примере. Рассмотрим систему,
состоящую из одной материальной точки,
которая должна оставаться на поверхности
f(x,
y,
z,
t)
= 0. Пусть в момент времени t
точка занимает положение P0
с координатами x0,
y0,
z0.
Мысленно дадим точке бесконечно малое
перемещение
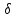 r
= (
r
= ( x,
x,
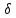 y,
y,
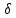 z).
Тогда ее координаты примут значения x0
+
z).
Тогда ее координаты примут значения x0
+
 x,
y0
+
x,
y0
+
 y,
z0
+
y,
z0
+
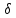 z.
Но не всякое
z.
Но не всякое
 r
не нарушает связи. Если смещенная точка
остается на поверхности, то
r
не нарушает связи. Если смещенная точка
остается на поверхности, то
 x,
x,
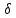 y,
y,
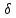 z
должны удовлетворять уравнению f(x0
+
z
должны удовлетворять уравнению f(x0
+
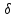 x,
y0
+
x,
y0
+
 y,
z0
+
y,
z0
+
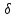 z,
t)
= 0. Разлагая его левую часть в ряд Тейлора,
получаем соотношение
z,
t)
= 0. Разлагая его левую часть в ряд Тейлора,
получаем соотношение
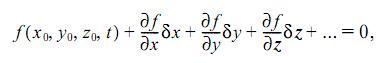
где
частные производные вычисляются в точке
P0,
а многоточие обозначает члены выше
первого порядка малости относительно
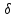 x,
x,
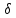 y,
y,
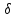 z.
Если этими членами пренебречь и
учесть, что f(x0,
y0,
z0,
t)
= 0, то придем к уравнению
z.
Если этими членами пренебречь и
учесть, что f(x0,
y0,
z0,
t)
= 0, то придем к уравнению

определяющему
виртуальные перемещения. Уравнение
(1), в частности, показывает, что в отличие
от действительного перемещения, которое
единственно, число виртуальных
перемещений бесконечно: мы имеем одно
линейное уравнение (1) относительно
трех неизвестных
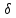 x,
x,
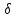 y,
y,
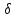 z.
Любой бесконечно малый вектор, имеющий
начало в точке P0
и лежащий в плоскости, касательной
к поверхности f
= 0, будет задавать виртуальное перемещение.
z.
Любой бесконечно малый вектор, имеющий
начало в точке P0
и лежащий в плоскости, касательной
к поверхности f
= 0, будет задавать виртуальное перемещение.
Бесконечно
малые приращения
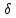 xv,
xv,
 yv,
yv,
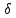 zv,
называются еще вариациями
величин xv,
yv,
zv.
Переход при фиксированном времени
t
из положения системы, определяемого
радиусами-векторами rv,
в бесконечно близкое положение,
определяемое радиусами-векторами
rv
+
zv,
называются еще вариациями
величин xv,
yv,
zv.
Переход при фиксированном времени
t
из положения системы, определяемого
радиусами-векторами rv,
в бесконечно близкое положение,
определяемое радиусами-векторами
rv
+
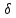 rv,
называют синхронным
варьированием.
rv,
называют синхронным
варьированием.
Если система свободная, то ускорения av ее точек определяются из второго закона Ньютона: mv av = Fv, где Fv — равнодействующая сил, приложенных к точке Pv. Если же система несвободная, то на ускорения ее точек наложены вполне определенные ограничения. Величины av не будут, вообще говоря, удовлетворять этим ограничениям, то есть ускорения wv точек Pv несвободной системы будут отличаться от их ускорений av в случае свободной системы, у точки Pv появляется дополнительное ускорение wv - av. Это ускорение возникает за счет неизвестных сил, обусловленных наличием связей. Их называют реакциями связей. Силы Fv называют активными силами. Они являются известными функциями координат и скоростей точек системы, а также, возможно, и времени t.
Обозначив через Rv равнодействующую реакций связей, приложенных к точке Pv, согласно второму закону Ньютона получим mv (wv - a) = Rv. Отсюда и из равенств mv av = Fv следуют уравнения движения точек системы
mvwv = R + Fv, v = 1, 2, …, N.
Связи называются идеальными, если работа реакций этих связей на любых виртуальных перемещениях равна нулю, то есть
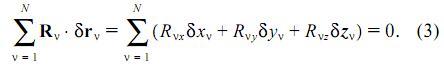
Примерами систем с идеальными связями могут служить следующие системы: материальная точка на абсолютно гладкой поверхности; свободное твердое тело; тело, вращающееся вокруг неподвижной оси; два тела, соединенные точечным шарниром; два соприкасающихся тела при отсутствии проскальзывания; две точки, соединенные невесомой нерастяжимой нитью, не оказывающей сопротивления изменению ее формы (идеальная нить). Многие материальные объекты в природе и технике с приемлемой для практики точностью можно моделировать системой с идеальными связями. Далее рассматриваются только такие системы.
