ВОПРОС 19-28 динамика

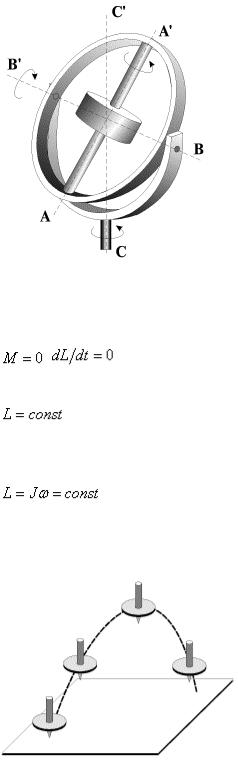
ВОПРОС 19

Тяжелый гироскоп — это волчок, т.е. симметричное твердое тело, вращающееся вокруг своей оси. Замечательным его свойством является то, что ось волчка сохраняет свою ориентацию в окружающем пространстве независимо от того, как перемещается аппарат, внутри которого помещен гироскоп (например, ракета). Это важный прибор, применяемый в навигационной технике, в системе ориентации летательных аппаратов в окружающем пространстве. Уравнения движения тяжелого твердого тела изучаются сегодня методами теории дифференциальных уравнений, симплектической геометрии, алгебры и топологии. Если твердое тело имеет «произвольную» форму, т.е. не обладает никакими симметриями, его движение будет хаотичным, тело будет беспорядочно кувыркаться в пространстве.

Гироскоп - это массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

В этом случае моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю. Это можно реализовать, например, поместив гироскоп в карданов подвес, изображенный на рис.89.

Рис.89
При этом
,	,	(1)

и момент импульса сохраняется:

(2)

Гироскоп ведет себя так же, как и свободнее тело вращения. В зависимости от начальных условий возможны два варианта поведения гироскопа:

1. Если гироскоп раскручен вокруг оси симметрии, то направления момента импульса и угловой скорости совпадают:

(3)

и направление оси симметрии гироскопа остается неизменным. В этом можно убедиться, поворачивая подставку, на которой расположен карданов подвес - при произвольных поворотах подставки ось гироскопа сохраняет неизменное направление в пространстве. По этой же причине волчок, "запущенный" на листе картона и подброшенный вверх (рис.90), сохраняет направление своей оси во время полета, и, падая острием на картон, продолжает устойчиво вращаться, пока не израсходуется запас его кинетической энергии.

Рис.90

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

(4)

Если интервал времени 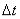мал, то и 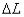мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется "затвердевшим".

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 91). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.

Рис.91

2. Если свободный гироскоп раскручен так, что вектор мгновенной угловой скорости и ось симметрии гироскопа не совпадают (как правило, это несовпадение при быстром вращении бывает незначительным), то наблюдается движение, описанное как "свободная регулярная прецессия".

Применительно же к гироскопу его называют нутацией. При этом ось симметрии гироскопа, векторы 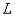и лежат в одной плоскости, которая

вращается вокруг направления с угловой скоростью, равной 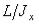где 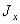- момент инерции гироскопа относительно главной центральной оси, перпендикулярной оси симметрии. Эта угловая скорость (назовем ее скоростью нутации) при быстром собственном вращении гироскопа оказывается достаточно большой, и нутация воспринимается глазом как мелкое дрожание оси симметрии гироскопа.

Нутационное движение легко продемонстрировать с помощью гироскопа, показанного на рис. 91 - оно возникает при ударах молотком по стержню

вращающегося вокруг своей оси гироскопа. При этом чем сильнее раскручен гироскоп, тем больше его момент импульса 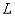- тем больше скорость нутации и тем "мельче" дрожания оси фигуры. Этот опыт демонстрирует еще одну характерную особенность нутации - с течением времени она постепенно уменьшается и исчезает. Это - следствие неизбежного трения в опоре гироскопа.

Наша Земля - своего рода гироскоп, и ей тоже свойственно нутационное движение. Это связано с тем, что Земля несколько приплюснута с полюсов, в силу

чего моменты инерции относительно оси симметрии 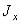и относительно оси, лежащей в экваториальной плоскости различаются. При

этом 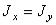а . В системе отсчета, связанной с Землей, ось вращения движется по поверхности конуса вокруг оси

симметрии Земли с угловой скоростью , то есть она совершает один оборот примерно за 300 дней. На самом деле в силу, как предполагается, неабсолютной жесткости Земли, это время оказывается больше - оно составляет около 440 суток. При этом расстояние точки земной поверхности, через которую проходит ось вращении, от точки, через которую проходит ось симметрии (Северный полюс), равно всего нескольким метрам. Нутационное движение Земли не затухает - по-видимому, его поддерживают сезонные изменения, происходящие на поверхности

ВОПРОС 20

При воздействии момента внешней силы вокруг оси, перпендикулярной оси вращения ротора, гироскоп начинает поворачиваться вокруг оси прецессии, которая перпендикулярна моменту внешних сил.

Поведение гироскопа в инерциальной системе отсчёта описывается, согласно следствию второго закона Ньютона, уравнением

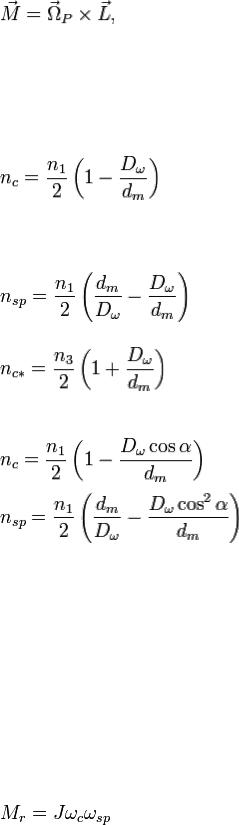
где векторы 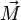и 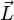являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса.

Изменение вектора момента импульса 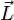под действием момента силы возможно не только по величине, но и по направлению. В частности, момент силы 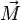, приложенный перпендикулярно оси вращения гироскопа, то есть перпендикулярный , приводит к движению, перпендикулярному

как 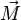, так и , то есть к явлению прецессии. Угловая скорость прецессии 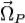гироскопа определяется его моментом импульса и моментом приложенной силы[9]:

то есть 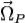обратно пропорциональна скорости вращения гироскопа. Одновременно с возникновением прецессии, согласно следствию третьего закона Ньютона, гироскоп начнёт действовать на окружающие его тела моментом реакции, равным по величине и противоположным по направлению

моменту 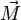, приложенному к гироскопу. Этот момент реакции называется гироскопическим моментом.

Подшипник представляет собой по существу планетарный механизм, в котором водилом является сепаратор, функции центральных колес выполняют внутреннее и наружное кольца, а тела качения заменяют сателлиты.

Частота вращения сепаратора или частота вращения шариков вокруг оси подшипника

где n1 — частота вращения внутреннего кольца радиального шарикоподшипника, Dω — диаметр шарика,

dm = 0,5(D+d) — диаметр окружности осей шариков.

Частота вращения шарика относительно сепаратора

Частота вращения сепаратора при вращении наружного кольца

где n3 — частота вращения внешнего кольца радиального шарикоподшипника.

Для радиально-упорного подшипника

Из приведенных выше соотношений следует, что при вращении внутреннего кольца сепаратор вращается в ту же сторону. Частота вращения сепаратора зависит от диаметра Dω шариков при неизменном dm: она возрастает при уменьшении Dω и уменьшается при увеличении Dω.

В связи с этим разноразмерность шариков в комплекте подшипника является причиной повышенного износа и выхода из строя сепаратора и подшипника в целом.

При вращении тел качения вокруг оси подшипника на каждое из них действует нагружающая дополнительно дорожку качения наружного кольца центробежная сила

,

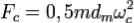где m — масса тела качения,

ωс — угловая скорость сепаратора.

Центробежные силы вызывают перегрузку подшипника при работе на повышенной частоте вращения, повышенное тепловыделение (перегрев подшипника) и ускоренное изнашивание сепаратора. Всё это сокращает срок службы подшипника.

В упорном подшипнике, кроме центробежных сил, на шарики действует обусловленный изменением направления оси вращения шариков в пространстве гироскопический момент

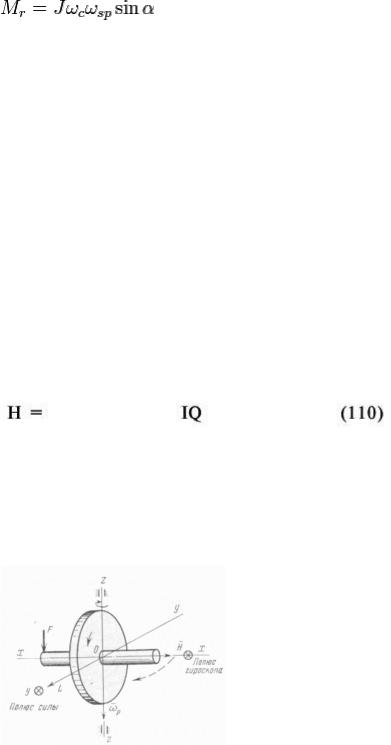
Гироскопический момент будет действовать на шарики и во вращающемся радиально-упорном шарикоподшипнике при действии осевой нагрузки

где — полярный момент инерции массы шарика; ρ — плотность материала шарика;

ωsp и ωс — соответственно, угловая скорость шарика при вращении вокруг своей оси и вокруг оси вала (угловая скорость сепаратора).

Под действием гироскопического момента каждый шарик получает дополнительное вращение вокруг оси, перпендикулярной плоскости, образованной векторами угловых скоростей шарика и сепаратора. Такое вращение сопровождается изнашиванием поверхностей качения, и для предотвращения

вращения подшипник следует нагружать такой осевой силой, чтобы соблюдать условие 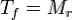, где Tf - момент сил трения от осевой нагрузки на площадках контакта шариков с кольцами.

ВОПРОС 21

Гироскоп, у которого возможны вращения вокруг трех указанных осей, называется гироскопом с тремя степенями свободы. Точка пересечения этих осей называется точкой подвеса гироскопа. Гироскоп с тремя степенями свободы, у которого центр тяжести всей системы, состоящей из ротора и карданных колец, совпадает с точкой подвеса, называется уравновешенным, или астатическим, гироскопом.

Уравновешенный гироскоп, к которому не прикладываются внешние вращающие моменты, называется свободным гироскопом.

Свободный гироскоп благодаря быстрому вращению приобретает свойства, широко используемые во всех гироскопических приборах. Основными свойствами свободного гироскопа являются свойства устойчивости и прецессии.

Первое состоит в том, что главная ось свободного гироскопа стремится сохранить первоначально заданное ей направление относительно мирового пространства. Устойчивость главной оси тем больше, чем точнее центр тяжести системы совпадает с точкой подвеса, чем меньше силы трения в осях карданова подвеса и чем больше вес гироскопа, его диаметр и скорость вращения. Величина, которая характеризует гироскоп с этой качественной стороны, называется кинетическим моментом гироскопа и определяется произведением момента инерции гироскопа на его угловую скорость вращения, т. е.

где I—момент инерции ротора гироскопа;

Q — угловая скорость вращения.

При конструировании гироскопических приборов стремятся достигнуть значительной величины кинетического момента Н путем придания ротору гироскопа особого профиля, а также путем увеличения угловой скорости его вращения. Так, в современных гирокомпасах роторы гиромоторов имеют скорость вращения от 6000 до 30 000 об/мин.

Рис. 121.

Устойчивость оси свободного гироскопа дает возможность использовать его в качестве прибора для обнаружения суточного вращения Земли, так как по отношению к земным предметам ось гироскопа будет совершать кажущееся или видимое движение.

Впервые это свойство гироскопа демонстрировалось известным французским физиком Леоном Фуко в 1852 г. Ему же принадлежит идея использования гироскопа в качестве прибора для определения направления движения и для определения широты судна в море.

Свойство прецессии состоит в том, что под действием силы, приложенной к кардановым кольцам, главная ось гироскопа перемещается в плоскости, перпендикулярной к направлению действия силы (рис. 121).

Такое движение гироскопа называется прецессионным. Прецессионное движение будет происходить в течение всего времени действия внешней силы и прекращается с прекращением ее действия. Направление прецессионного движения определяется с помощью правила полюсов, которое формулируется следующим образом: при приложении к гироскопу момента внешней силы полюс гироскопа кратчайшим путем стремится к полюсу силы. Полюсом гироскопа называется тот конец его главной оси, со стороны которого вращение гироскопа наблюдается происходящим против часовой стрелки. Полюсом

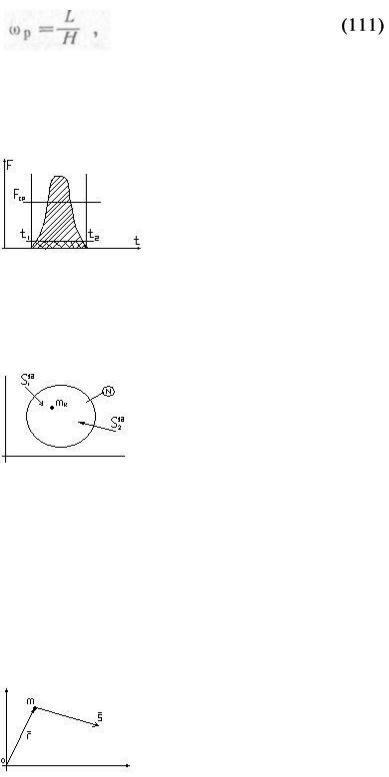
силы называется тот конец оси гироскопа, относительно которой приложенная внешняя сила стремится повернуть гироскоп против часовой стрелки.

На рис. 121 прецессионное движение гироскопа указано стрелкой.

Угловая скорость прецессии может быть подсчитана по формуле

ВОПРОС 22

Удар - механическое явление, при котором за малый промежуток времени скорости части точек системы изменяются на конечные величины.

1. ∆τ - время удара (очень мало - тысячные доли секунды) ∆V/∆τ = aср - велик

Fсруд = maср => Fсруд - очень велика

2.< S > = t1∫t2< F >dt

S/∆τ = Fсруд

3.Пренебрежем Sнеуд mU - mV = ∆τ∫ Fудdt = Sуд m (U-V) = Sуд

S // (U-V)

Изменение количества движения точки за время удара равно импульсу, приложенному к точке.

mkUk - mkVk = Sk(e) - Sk(i), k=1...N

Изменение количества движения механической системы за время удара равно векторной сумме внешних ударных импульсов.

∑mkUk - ∑mkVk = ∑Sk(e) + ∑Sk(i)

Q - Q0 = ∑Sk(e)

Qx - Q0x = ∑Skx(e)

Q = MUc, Q0 = MVc

M(Uc - Vc) = ∑Sk(e)

a) ∑Sa(e) = 0

Q - Q0 = const.

б) ∑Skx(e) = 0; ∑ Sky(e) = 0; ∑ Skz(e)

= 0

Qx = Q0

r(mU - mV) = rS rmU - rmV = rS

rkx(mkUk) = rk(Sk(e) + Sk(i))

∑rkmkUk - ∑rkmkVk = ∑M0(Sk(e)) + ∑M0(Sk(i))

K0 - K0(0) = ∑M0(Sk(e))

Kz - Kz(0) = ∑Mz(Sk(e))

Твердое тело

Iz (w - w0) = ∑Mz(Sk(e)) если ∑M0(Sk(e))=0 => K0 = K0(0) = const.

Kz = Kz0 => тв.т w=w0

Теорема об изменении кинетической энергии при ударе (Теорема Кельвина)

mU - mV = S

mU2 - mV2 = S(U+ V)

(mU2)/2 - (mV2/2 = S(U + V)/2

T - T0 = S(U + V)/2

Работа силы, приложенной к материальной точке за какой-либо промежуток времени равна скалярному произведению импульса силы на полусуммы начальной и конечной скоростей точек.

Sk = Sk(e) + Sk(i)

T - T0 = 1/2*∑[(Sk(e) + Sk(i))(Uk + Vk)]

ВОПРОС 23

При неабсолютно упругом (или просто неупругом) ударе для нахождения решения используют понятие коэффициента восстановления при ударе.

Коэффициент восстановления в теории удара — величина, зависящая от упругих свойств соударяющихся тел и определяющая, какая доля начальной относительной скорости этих тел восстанавливается к концу удара. Коэффициент восстановления. характеризует потери механической энергии соударяющихся тел вследствие появления в них остаточных деформаций и их нагревания[7]. Обычно коэффициент восстановления определяется по отскоку тела от массивной плиты. При этом коэффициент, в частности, равен[8]

дерево о дерево ½;

сталь о сталь 5/9;

слоновая кость о слоновую кость 8/9;

стекло о стекло 15/16.

При неупругом центральном ударе двух тел, учитывая, что удар зависит от разности скоростей, коэффициент восстановления определяется соотношением[5]

Потеря энергии при неупругом ударе определяется выражением[9]:

При нецентральном ударе в пренебрежении трением коэффициент восстановления определяется только для проекций скоростей, перпендикулярных поверхности касания тел[

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом:

1.Есть в наличии два абсолютно твердых тела, которые сталкиваются

2.В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.

3.В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.

4.Контакт тел прекращается и они продолжают движение.

Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.

Здесь m1, m2 - массы первого и второго тел. u1, v1 - скорость первого тела до, и после взаимодействия. u2, v2 - скорость второго тела до, и после взаимодействия.

Важно - импульсы складываются векторно, а энергии скалярно.

Абсолю́тно неупругий́ удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Где v это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения. mb - масса второго тела, ub - скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно.

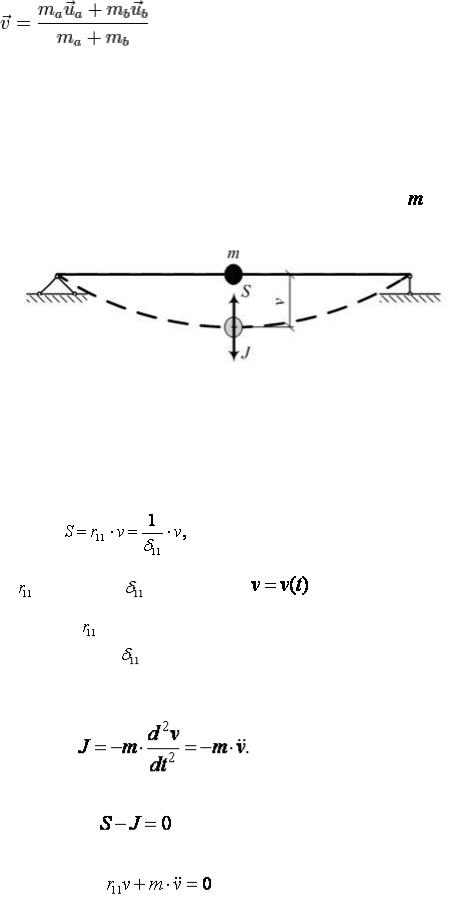
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит втепловую.

Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

ВОПРОС 24

Свободные колебания консервативных систем с одной степенью свободы

Рассмотрим систему с одной степенью свободы в виде невесомой балки с сосредоточенной массой	(рис. 2.1). Если систему вывести из состояния
равновесия, то она будет совершать свободные колебания.

Рис. 2.1. Система с одной степенью свободы

Для составления уравнения движения массы используем принцип Даламбера. В любой момент времени на массу действует сила упругости системы и силы инерции. Силы сопротивления среды, которые приводят к затуханию свободных колебаний, в данном случае не учитываются.

Сила упругости системы 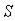, которая пропорциональна отклонению массы от положения равновесия, определяется выражением

				(2.1)
где	– жесткость системы;		– податливость системы;	– отклонение массы от положения статического равновесия.
Жесткость системы		представляет силу, которую необходимо приложить в точке прикрепления массы, чтобы вызвать единичное перемещение этой

точки. Податливость системы – величина обратная жесткости и представляет перемещение точки, вызванное единичной силой.

Сила инерции 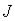направлена в сторону, противоположную ускорению, и определяется выражением:

(2.2)

Масса в процессе свободных колебаний будет находиться в равновесии под действием силы упругости и силы инерции

(2.3)

Сделав подстановку величин, получим

,

или

,

,

(2.4)

где

. (2.5)

Интегралом дифференциального уравнения свободных колебаний является функция (2.4)

		(2.6)
Постоянные	и	, входящие в уравнение (2.6), определяются при начальных условиях	,	,	и равны

;.

Теперь уравнение (2.6) запишется в виде

. (2.7)

Если в начальный момент времени	, то уравнение (2.7) принимает вид		.
(2.8)
Уравнение (2.6) можно представить в другом виде. Для этого выразим		и	через новые постоянные следующим образом:

;

Тогда уравнение свободных гармонических колебаний системы с одной степенью свободы запишется в виде

(2.9)

где	амплитуда колебаний,

начальная фаза колебаний.

График свободных колебаний приведен на рис. 2.2.

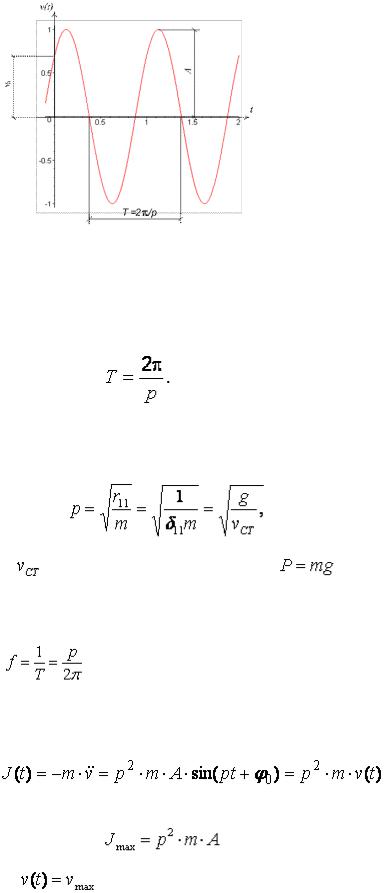
Рис. 2.2. График свободных колебаний

Из графика видно, что величина 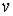меняет знак и в определенные моменты достигает наибольших отклонений (амплитуд). Время 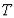, за которое масса совершает один полный цикл, называется периодом и определяется выражением:

(2.10)

Величина, обратная периоду колебаний, определяет число циклов колебаний в единицу времени и называется частотой. Частоту 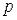, равную числу циклов колебаний в 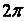секунд, называют круговой частотой колебаний и определяют по формуле:

(2.11)

где

– перемещение точки при статическом приложении силы

.

Единицей измерения круговой частоты 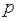служит 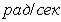, которую часто записывают . Число циклов колебаний за одну секунду называют технической частотой и определяют по формуле

(2.12)

За единицу измерения технической частоты колебаний принимается – одно колебание за секунду.

Сила инерции в произвольный момент времени определяется выражением

. (2.13)

При гармонических колебаниях сила инерции пропорциональна отклонению массы и достигает своего максимального (амплитудного) значения

(2.14)

при

.

Свободные колебания характеризуются непрерывным переходом кинетической энергии движения массы в потенциальную энергию деформации системы и наоборот.

ВОПРОС 25

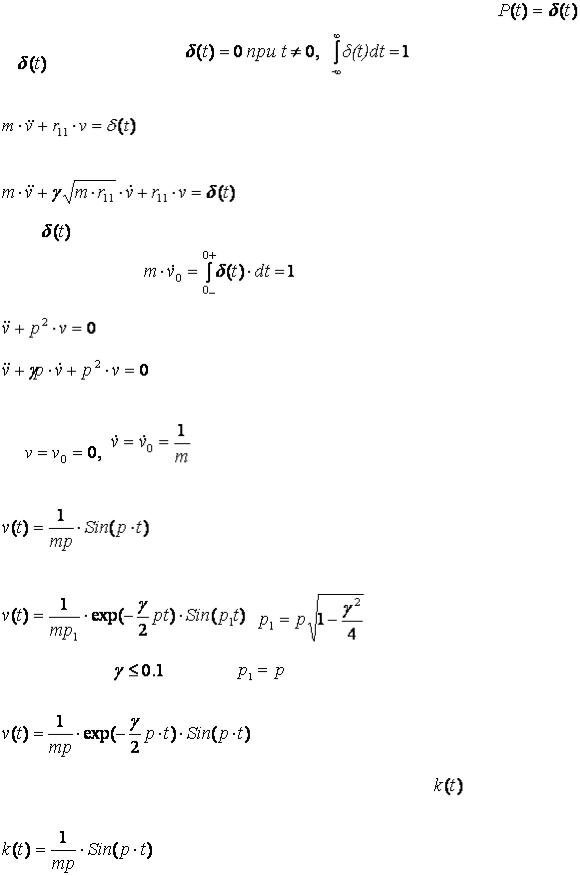
Вынужденные колебания системы с одной степенью свободы

2.3.1. Импульсная переходная функция

Рассмотрим вынужденные колебания упругой системы с одной степенью свободы на действие возмущающей нагрузки				,
где	– обобщенная функция Дирака:		.
Теперь уравнение движения консервативной системы представляется так
	.	(2.23)
Уравнение движения диссипативной системы, подчиняющейся скорректированной модели Фохта, имеет вид
		.	(2.24)
Нагрузка	есть математическая запись воздействия единичного импульса на систему в момент времени t = 0. Запишем закон сохранения
импульса в момент времени t = 0:			. При t > 0 уравнения (2.23), (2.24) имеют вид (2.4) и (2.17):
	,

с начальными условиями:

t = 0, . (2.25)

Решение уравнения (2.4) с начальными условиями (2.25) получим из (2.8)

.

(2.26)

Решение уравнения (2.17) с теми же начальными условиями получим из (2.18) с учетом (2.19), (2.20) и (2.25):

	,	.	(2.27)
Для реальных материалов	(см. табл. 2.1) и	, так что
с большой точностью можно считать

.	(2.28)
Формулы (2.26) – (2.28) называются импульсной переходной функцией (ИПФ) и обозначаются символом		. Таким образом, для консервативной
системы с одной степенью свободы

,(2.29)