ВОПРОС 10-18 динамика

ВОПРОС 10

Принцип Даламбера применяется для решения задач динамики несвободных механических систем.

Формулировка принципа: если к каждой точке несвободной механической системы помимо действующих активных сил и сил реакций приложить условную силу инерции, то образованная система сил будет уравновешенной.

Принцип Даламбера позволяет уравнениям динамики придать форму уравнений равновесия статики.

Уравнения принципа Даламбера для конкретной системы зависят от того, как расположены приложенные к этой системе силы ( активные, силы реакции и силы инерции ).

Уравнения принципа Даламбера имеют вид:

● если все силы сходятся в одной точке

,

,(5.1)

;

● если силы произвольно расположены в одной плоскости

,

,(5.2)

;

● если силы расположены в произвольной пространственной системе

		,
		,
		,	(5.3)
			,
			,
			,
где	– активная сила, приложенная к	-й точке;	– сила реакции, приложенная к	-й точке;	– сила инерции, приложенная к	-й
точке.

Уравнения принципа Даламбера, как и уравнения статики, могут быть составлены для любых точки и твердого тела, входящих в механическую систему, а также для системы в целом, т. е. как и в статике уравнения принципа Даламбера составляются для выбранного объекта.

17.2. Приведение системы сил инерции твердого тела к простейшему виду

По теореме Пуансо систему сил инерции, приложенных к точкам твердого тела, в общем случае можно заменить силой и парой сил. Сила приложена в центре приведения и равна главному вектору сил инерции, момент пары равен главному моменту сил инерции относительно центра приведения.

Поскольку , , 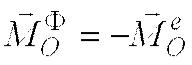применяя теорему о движении центра масс и теорему об

изменении кинетического момента, находим:			,		. Здесь за центр
приведения		принята произвольная неподвижная точка в инерциальной системе отсчета.		Обычно за центр приведения выбирается центр масс
механической системы.

Тогда с учетом теоремы об изменении кинетического момента в поступательно движущейся с центром масс системе

отсчета

,

.

Рассмотрим частные случаи движения твердого тела.

1) При поступательном движении твердого тела выбирая за центр приведения центр масс системы, находим, что главный момент сил инерции относительно центра масс равен нулю

.

То есть система сил инерции приводится к равнодействующей, которая приложена в центре масс и определяется

равенством		.
2) При вращении тела, имеющего плоскость материальной симметрии, вокруг оси, проходящей через центр масс перпендикулярно этой
плоскости выбирая за центр приведения неподвижную точку (рис. 17.3), совпадающую с центром масс, находим, что				. Система сил
приводится к паре сил, лежащей в плоскости материальной симметрии тела. Вектор момента этой пары определяется

равенством		. Алгебраический момент пары сил инерции может быть
вычислен по формулам:

.

3) При плоском движении твердого тела, имеющего плоскость материальной симметрии в качестве центра приведения выбираем центр масс, расположенный в плоскости симметрии тела, которая перемещается в координатной

плоскости (рис. 17.4). Так как плоское движение

может быть представлено как сложение поступательного

движения с центром масс и вращательного вокруг оси

, проходящей через центр масс, то система сил инерции приводится к силе и к паре,

лежащей в плоскости материальной симметрии		,		, где	−
момент инерции относительно оси, проходящей через центр масс, перпендикулярно плоскости материальной симметрии.

4) Аналогично рассматривается приведение системы сил инерции при вращении тела, имеющего плоскость материальной симметрии, вокруг оси, не проходящей через центр масс. При этом за центр приведения может выбираться как центр масс, так и неподвижная точка на оси вращения (рис. 17.5).

Если в качестве центра приведения принимается точка , лежащая на оси вращения в плоскости симметрии, то главный момент сил инерции

равен ,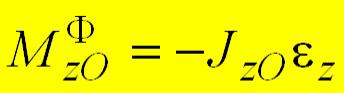

где - момент инерции тела относительно оси вращения .

ВОПРОС 11

А для уравновешенной системы сил уже в соответствии с принципом возможных перемещений сумма виртуальных работ сил на любом возможном перемещении системы должна быть равна нулю.

Сформулировать записанное можно следующим образом.

В любой момент движения механической системы с идеальными связями сумма виртуальных работ активных сил и сил инерции на любом возможном перемещении системы равна нулю.

Это равенство принято называть

общим уравнением динамики или принципом Лагранжа-Даламбера.

ВОПРОС 12

Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.

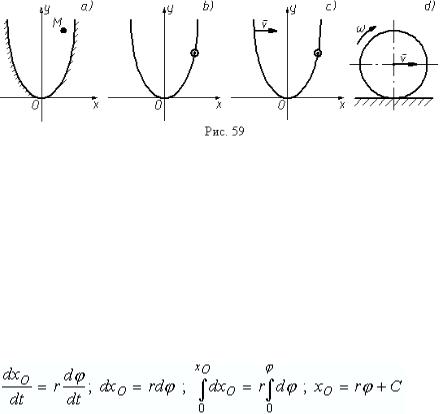
Связи разделяются на удерживающие и неудерживающие. Если связь описывается неравенством, то она называется неудерживающей. На рис. 59,a

показана материальная точка, движение которой ограничивается квадратичной параболой, то есть связь описывается неравенством y ax2. Если связь описывается равенством, например y = ax2 для бусинки надетой на проволоку, изогнутую в виде квадратичной параболы (рис. 59, b), то связь называется удерживающей.

Математическое выражение, описывающее удерживающую связь, является уравнением связи. В общем случае уравнение связи, налагаемой на точку системы, записывается в виде

Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь,

уравнение которой имеет вид 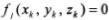, является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким: .

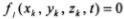Например, жесткий стержень длиной l, прикрепленный к неподвижной опоре, является стационарной связью для материальной точки, находящейся на его свободном конце. Уравнение связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеет

вид .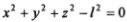

К голономным относятся все геометрические связи, а также те кинематические (дифференциальные) связи, которые путем интегрирования могут быть сведены к геометрическим. Так кинематическая связь, наложенная на колесо, является голономной, так как ее можно проинтегрировать и свести к геометрической:

где C - постоянная интегрирования. Кинематическая или дифференциальная связь, уравнение которой не может быть проинтегрировано,

называется неголономной.

Механическая система называется голономной, если все ее связи голономные, и неголономной, если хотя бы одна из ее связей является неголономной.

В дальнейшем мы будем, как правило, рассматривать материальные системы с удерживающими голономными связями, уравнение которых имеет вид

f(x, y, z, t) = 0

Идеа́льные свя́зи — класс связей, удовлетворяющих следующему условию: суммарная возможная работа всех реакций этих связей на любых возможных перемещениях равна нулю.

Аналитически сформулированное выше условие идеальности для системы материальных точек может быть сформулировано[1] так:

,

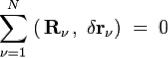где 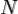— число точек, входящих в систему, 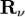— равнодействующая реакций связей, приложенных к 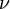-й точке, 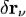— возможное перемещение данной точки (круглыми скобками обозначено скалярное произведение векторов).

Примеры идеальных связей:

1. Наложенная на материальную точку связь в виде гладкой поверхности (неподвижной или деформирующейся с течением времени), по которой должна двигаться точка (здесь возможные перемещения лежат в касательной плоскости к данной поверхности, а реакция связи этой плоскости ортогональна, так что скалярное произведение равно нулю).2. Внутренние связи в абсолютно твёрдом теле, обеспечивающие постоянство расстояний между текущими положениями точек тела.3. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении гладкими поверхностями.4. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении абсолютно шероховатыми поверхностями.

ВОПРОС 13

В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим возможную работу сил, приложенных к точкам системы,

Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.

ВОПРОС 14

Для вывода уравнений запишем принцип Даламбера-Лагранжа в обобщенных координатах в виде -Qju = Qj (j = 1 ÷ s).

Принимая во внимание, что Фi = -miai = -midVi / dt, получаем

(1)

Далее обобщенные силы инерции в левой части нужно выразить через кинетическую энергию. Это впервые сделал Лагранж, который доказал, что для систем с голономными связями обобщенные силы инерции равны

(2)

Подставляя (2) в (1) получаем дифференциальные уравнения движения системы в обобщенных координатах, которые названы уравнениями Лагранжа второго рода:

(3)

то есть, материальная система с голономными связями описывается уравнениями Лагранжа второго рода по всем s обобщенным координатам.

Отметим важные особенности полученных уравнений.

1.Уравнения (3) - это система обыкновенных дифференциальных уравнений второго порядка относительно s неизвестных функций qj(t), полностью определяющих движение системы.

2.Число уравнений равно числу степеней свободы, то есть движение любой голономной системы описывается наименьшим числом уравнений.

3.В уравнения (3) не нужно включать реакции идеальных связей, что позволяет, находя закон движения несвободной системы, выбором обобщенных координат исключить задачу определения неизвестных реакций связей.

4.Уравнения Лагранжа второго рода позволяют указать единую последовательность действий для решения многих задач динамики, которую часто называют формализмом Лагранжа.

Уравнения Лагранжа второго рода в случае потенциальных сил.

Если все силы системы потенциальны, то обобщенные силы системы выражаются через потенциальную энергию системы как Qj = -дП / дqj, а уравнения Лагранжа второго рода запишутся в виде

Так как потенциальная энергия не зависит от обобщенных скоростей, то . Введем в рассмотрение функцию

L = T - П

(4)

которую называют функцией Лагранжа или кинетическим потенциалом. Тогда уравнения Лагранжа в случае потенциальных сил запишутся так:

(5)

Если среди сил системы вместе с потенциальными присутствуют непотенциальные силы, например силы трения, то обобщенные силы системы складываются из обобщенных потенциальных сил Qjn = -дП / дqj и обобщенных непотенциальных сил Qj, а уравнения (3) принимают вид

(6)

При обобщении понятий функции, аналогичные функциям Лагранжа, описывают состояние не только механических систем, но и систем иной физической природы, например, непрерывной среды, гравитационного, электростатического или электромагнитного поля и т.д.

Таким образом, уравнения Лагранжа второго рода (3) и (5) являются наиболее универсальными, наиболее общими уравнениями движения материальных систем. Они используются не только в теоретической механике и в ее приложениях, но и в других науках, в частности в теоретической физике, электротехнике и теории управления.

ВОПРОС 16

Если голономная механическая система описывается лагранжианом 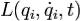( 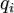— обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы.

Понятие функции Лагранжа было первоначально введено для переформулировки классической механики в виде, известном как лагранжева механика. В этом контексте функция Лагранжа обычно берётся в виде разности кинетической и потенциальной энергии механической системы.

Пусть размерность пространства равна трём и функция Лагранжа записана в виде

где производная по времени обозначается точкой над дифференцируемой величиной, 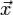— радиус-вектор частицы, m — её масса и V — потенциальная

энергия. Тогда уравнение Эйлера-Лагранжа будет: 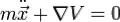, где 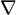— градиент.

Используя этот результат, можно легко показать, что этот подход эквивалентен подходу Ньютона. Запишем силу F в терминах

потенциала 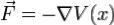, тогда мы получим уравнение 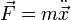, которое аналогично уравнению Ньютона с постоянной массой.

Простые вычисления приведут нас к выражению 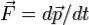, которое является вторым законом Ньютона в его обобщённой форме.

Для трёхмерной системы со сферическими координатами r, θ, φ с лагранжианом

можно получить следующие уравнения Эйлера-Лагранжа:

ВОПРОС 17

Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое

П = А (мо) (19.3.1)

Потенциальная энергия зависит от положения точки М, то есть от ее координат

П = П(х,у,z) (19.3.2)

Поясним здесь, что силовым полем называется часть пространственного объема, в каждой точке которого на частицу действует определенная по модулю и направлению сила, зависящая от положения частицы, то есть от координат х, у, z. Например, поле тяготения Земли.

Функция U от координат, дифференциал которой равен работе, называется силовой функцией. Силовое поле, для которого существует силовая функция,

называется потенциальным силовым полем, а силы действующие в этом поле, - потенциальными силами.

Пусть нулевые точки для двух силовых функций П(х,у,z) и U(x,y,z) совпадают.

По формуле (14.3.5) получаем 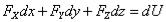, т.е. dA = dU(x,y,z) и

где U - значение силовой функции в точке М. Отсюда

П(x,y,z) = -U(x,y,z) (19.3.5)

Потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком.

То есть, при рассмотрении свойств силового поля вместо силовой функции можно рассматривать потенциальную энергию и, в частности, уравнение (19.3.3) перепишется как

Работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном положении.

В частности работа силы тяжести:

Часть пространства, в которой на помещенную туда материальную точку действует сила, зависящая от места положения точки, называется силовым полем.

Причем, эта сила определяется с помощью силовой функции u = u(x, y, z). Если она не зависит от времени, то такое поле называется стационарным. Если во всех точках она одинакова, то поле – однородное.

Если же проекции силы на декартовы оси есть частные производные от силовой функции по соответствующим координатам

,

,

,

(6)

то такое поле называется потенциальным.

Вычислим работу силы потенциального поля при перемещении точки из положения М1 в положение М2. (рис. 23).

Рис.23

Элементарная работа,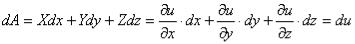

Это есть полный дифференциал силовой функции.

Работа на конечном перемещении

(7)

где u2 и u1 – значения силовой функции в точках М2 и М1.

Следовательно, работа силы потенциального поля не зависит от траектории движения точки, а определяется лишь значениями силовой функции в начальном и конечном положениях точки.

Естественно, если точка вернется в начальное положение, работа силы 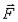будет равна нулю. Работа окажется равной нулю и при переходе в другую точку М3, если там значение силовой функции будет такое же, как и в начальном положении.

Нетрудно догадаться, что точки с одинаковыми значениями силовой функции будут образовывать целую поверхность. И что силовое поле – это слоеное пространство, состоящее из таких поверхностей (рис. 23). Эти поверхности называются поверхностями уровня илиэквипотенциальными поверхностями. Уравнения их: u(x, y, z)=C (C – постоянная, равная значению u в точках этой поверхности). А силовую функцию называют,

соответственно, потенциалом поля.

Конечно, эквипотенциальные поверхности не пересекаются. Иначе существовали бы точки поля с неопределенным потенциалом.

Поскольку, при перемещении точки по эквипотенциальной поверхности работа силы 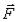равна нулю, то вектор силы перпендикулярен поверхности.

Выберем среди этих поверхностей какую-нибудь одну и назовем ее нулевой поверхностью (положим у нее u=u0).

Работа, которую совершит сила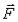при переходе точки из определенного места М на нулевую поверхность, называют потенциальной энергией точки в этом определенном месте М:

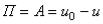. (8)

Заметим, что потенциальная энергия в одной и той же точке поля зависит от выбора нулевой поверхности.

По (8) силовая функция 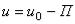. Поэтому проекции силы на декартовы оси, по (6), так как ,

;

;

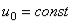(9)

и вектор силы .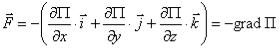

Рассмотрим несколько потенциальных полей.

1) Поле силы тяжести.

Вблизи поверхности Земли сила тяжести во всех точках одинакова , равна весу тела. Значит, это силовое поле однородное. Так как при перемещении точки в горизонтальной плоскости работа силы равна нулю, то эквипотенциальными поверхностями будут горизонтальные плоскости (рис. 24), а уравнения их: u = z = C.

Рис.24

Если нулевой поверхностью назначить плоскость xOy, то потенциальная энергия точки в положении М будет равна работе силы тяжести:

.

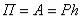2) Поле упругой силы.

При деформации упругого тела, например пружины, появляется сила. То есть около этого тела возникает силовое поле, силы которого пропорциональны деформации тела и направлены в сторону недеформированного состояния. У пружины – в точку М0, где находится конец недеформированной пружины

(рис. 25).

Рис.25

Если перемещать конец пружины так, чтобы длина ее не изменялась, то работа упругой силы 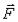будет равна нулю. Значит эквипотенциальными поверхностями являются сферические поверхности с центром в точке О.

Назначим нулевой поверхностью сферу, проходящую через точку М0, через конец недеформированной пружины. Тогда потенциальная энергия пружины в

положении М: .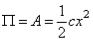

При таком выборе нулевой поверхности потенциальная энергия всегда будет положительной (П>0), и в растянутом, и в сжатом состоянии.

ВОПРОС 18

Согласно принципу возможных перемещений (основному уравнению статики), для того, чтобы механическая система, на которую наложены идеальные, стационарные, удерживающие и голономные связи, находилась в равновесии, необходимо и достаточно, чтобы в этой системе были равны нулю все обобщенные силы:

(1)

где Qj - обобщенная сила, соответствующая j - ой обобщенной координате;

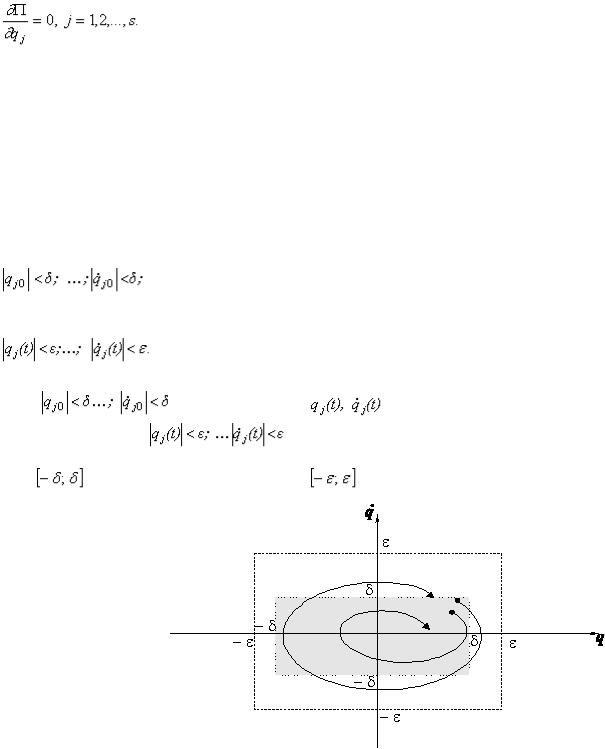
s - число обобщенных координат в механической системе.

Если для исследуемой системы были составлены дифференциальные уравнения движения в форме уравнений Лагранжа II - го рода, то для определения возможных положений равновесия достаточно приравнять обобщенные силы нулю и решить полученные уравнения относительно обобщенных координат.

Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений (1) получаем следующие условия равновесия:

(2)

Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие, определяемое вышеприведенными формулами, может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения.

Определение понятия устойчивости положения равновесия было дано в конце XIX века в работах русского ученого А. М. Ляпунова. Рассмотрим это определение.

Для упрощения выкладок условимся в дальнейшем обобщенные координаты q1, q2,..., qs отсчитывать от положения равновесия системы:

, где

Положение равновесия называется устойчивым, если для любого сколь угодно малого числа 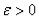можно найти такое другое число ,

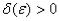что в том случае, когда начальные значения обобщенных координат и скоростей не будут превышать :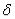

значения обобщенных координат и скоростей при дальнейшем движении системы не превысят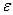

Иными словами, положение равновесия системы q1 = q2 = ...= qs = 0 называется устойчивым, если всегда можно найти такие достаточно малые начальные

значения		, при которых движение системы	не будет выходить из любой заданной сколь угодно малой
окрестности положения равновесия		. Для системы с одной степенью свободы устойчивое движение системы можно
наглядно изобразить в фазовой плоскости (рис.77). Для устойчивого положения равновесия движение изображающей точки, начинающееся в
области	, не будет в дальнейшем выходить за пределы области		.

Рис.77

Положение равновесия называется асимптотически устойчивым, если с течением времени система будет приближаться к положению равновесия, то есть