ВОПРОС 1-9 динамика

ВОПРОС 1

В классической механике полным импульсом системы материальных точек называется векторная величина, равная

сумме произведений масс материальных точек на их скорости:.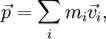

Если имеется материальная точка массой , двигающаяся со скоростью 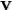и находящаяся в точке, описываемой радиус-вектором 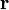, то момент импульса вычисляется по формуле:

где 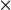— знак векторного произведения.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

Можно переписать это через плотность :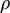

(Если считать, что 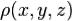— обобщенная функция, включающая, возможно, и дельтообразные члены, то последняя формула применима и к распределенным, и к дискретным системам).

Для систем, совершающих вращение как целое (как абсолютно твёрдое тело) вокруг одной из осей симметрии (или, обобщенно — вокруг так называемых главных осей инерции тела), справедливо соотношение

где 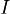— момент инерции относительно оси вращения, — вектор угловой скорости.

В общем случае вектор момента связан с вектором угловой скорости через линейный оператор момента инерции (тензор инерции):

За начало отсчета при вычислении моментов инерции или тензора инерции в принципе может быть взята любая ось или точка, при этом будут получены разные величины, связанные друг с другом через теорему Штейнера. Однако практически по умолчанию обычно выбирается центр масс или закрепленная ось (центр), что является чаще всего и более удобным.

ВОПРОС 2

Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса riсо скоростью vi . Скорость vi и импульс mivi перпендикулярны этому радиусу, т. е. радиус является плечом вектора mivi . Значит, мы можем записать, что момент импульса отдельной частицы равен

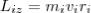(1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу vi = ωri, получим

т. е. 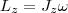2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство

(3)

В замкнутой системе момент внешних сил 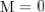и 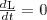откуда

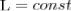(4)

Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Момент импульса относительно точки и оси:

,Рассмотрим механическую систему, состоящую из n материальных точек (в частности, это может быть и твердое тело, но мы пока такое ограничение накладывать не будем). Пусть mi и vi – масса и скорость i-й точки системы. Моментом импульса Li материальной точки относительно неподвижной точки О наз. векторное произведение радиуса-вектора ri материальной точки, проведенного из точки О, на импульс этой материальной точки pi=mivi (рис): Li=[rimivi]=[ripi] Соответственно, моментом импульса механической системы относительно неподвижной точки О наз. вектор L, равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы: L=(n| |i=1)Li=(n| |i=1)(ripi). Вектор, равный геометрической сумме моментов относительно точки О всех внешних сил, действующих на механическую систему, наз. главным моментом внешних сил относительно неподвижной точки О: Mвнеш=(n| |i=1)[riFiвнеш]. Моментом импульса механической системы относительно оси наз. проекция на эту ось вектора момента импульса системы относительно любой точки, выбранной на рассматриваемой оси. => моментом силы относительно оси наз. проекция на эту ось вектора момента силы относительно любой точки, выбранной на данной оси (выбор точки на оси влияет на значения моментов импульса). Производная по времени от момента импульса механич. сист. относит. её центра масс = главному моменту относительно той же точки всех внешних сил, дейсвующ. на сист.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что 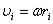, получим

.

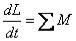
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):

.

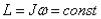Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:

.

ВОПРОС 3

Момент инерции материальной точки:

относительно данной оси – скалярная величина, равная произведению массы точки на квадрат расст. от этой точки до оси (J=mr2, m – масса точки; r – расстояние от точки до оси). Момент инерции сист. (тела) относительно оси – физическая величина, равная сумме масс n материальных точек сист. на квадраты их расст. до рассматриваемой оси (J=(n| |i=1)miri2). Момент энерции в случае непрерывного распределения масс (J=§r2dm, интегрирование производится по всему объёму тела. В данном случае r – функция положения точки с координатами x, y, z).

Тело	Положение оси	Момент
	вращения	инерции
Полн.	Ось симметрии	mR2
тонкостен.
цил. рад. R
Сплошн.	То же	(1/2)mR2
цил. или
диск рад. R
Прям. тонк.	Ось стерж. и проход.	(1/12)m
стерж.	через его серед.	l2
длин. l
То же	Ось стерж. и проход.	(1/3)m l2
	через его конец
Шар рад. R	Ось проход. через	(2/5)mR2
	центр шара

ВОПРОС 4

Кинетической энергией механической системы называется сумма кинетических энергий всех точек этой системы:

T = ∑ mkvk2 / 2 ,

где mk и vk - масса и скорость k-й материальной точки, принадлежащей данной системе.

На основании теоремы Кёнига кинетическая энергия произвольной механической системы определяется по формуле

T = MvC2/2 + ∑ mkvkr2 / 2 ,

где M - масса всей системы;

vC - скорость центра масс системы;

mk - масса k-й точки системы;

vkr - относительная скорость k-й точки при движении её вокруг центра масс

(т.е. vk= vC vkr).

Из этой формулы можно получить следующие частные случаи для твёрдого тела:

- при поступательном движении тела vk= vC , vkr= 0,

T = mvC2 / 2;

- при вращении тела вокруг оси, проходящей через его центр масс, vC=0 , vkr= ω rk,

T = ∑ mkvkr2 / 2 = Jω2/2 ,

где J - момент инерции тела относительно оси, проходящей в данный момент времени через центр масс;

ω - угловая скорость вращения тела;

- в случае произвольного движения тела (например при плоскопараллельном движении)

T = mvC2 / 2 + Jω2/2.

Рассмотрим точку с массой т, перемещающуюся под действием приложенных к ней сил из положения M0 , где она имеет скорость 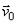, в положение М1 , где ее скорость равна 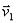.Для получения искомой зависимости обратимся к

уравнению 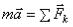выражающему основной закон динамики. Проектируя обе части этого равенства на касательную 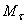к траектории точки М, направленную в сторону движения, получим:

Стоящую слева величину касательного ускорения можно представить в виде

.

В результате будем иметь:

.

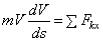Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что 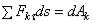где 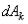- элементарная работа силы Fk получим выражение теоремы об изменении кинетической энергии в дифференциальной форме:

.

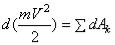Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M0 и M1, найдем окончательно:

.

Уравнение выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Абсолютно твердое тело — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

— масса тела

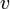— скорость центра масс тела

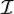— момент инерции тела

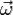— угловая скорость тела.

ВОПРОС 5

Теорема об изменении количества движения системы утверждает[2][3]:

Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.

Пусть система состоит из 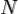материальных точек с массами 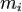и ускорениями 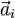. Все силы, действующие на тела системы, разделим на два вида:

Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил,

действующих на материальную точку с номером i обозначим .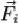

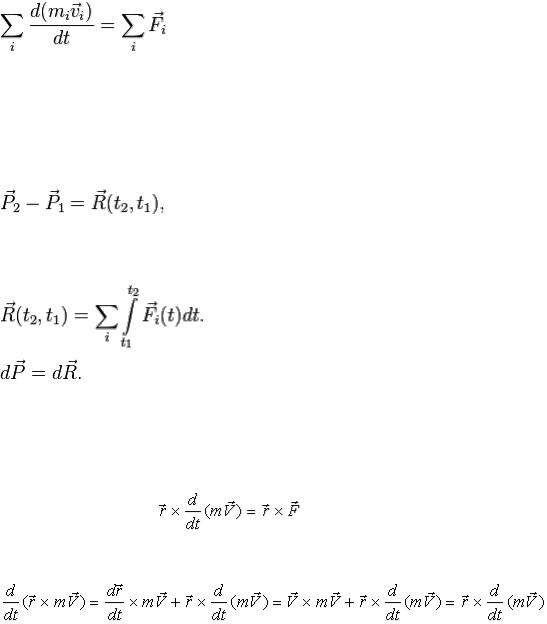
Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать 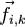, а силу воздействия i-й точки на k-ю точку — 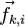. Очевидно, что при ,

то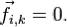

Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде

Учитывая, что 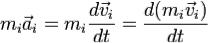и суммируя все уравнения второго закона Ньютона, получаем:

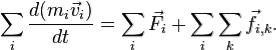Выражение 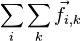представляет собой сумму всех внутренних сил,

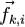действующих в системе. По третьему закону Ньютона в этой сумме каждой силе соответствует сила такая, что 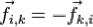и,

значит, выполняется 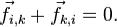Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать

.Используя для количества движения системы 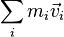обозначение 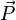, получим

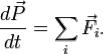Введя в рассмотрение изменение импульса внешних сил 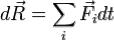, получим выражение теоремы об изменении количества движения системы в дифференциальной форме:

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторым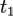и и 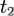, получим выражение теоремы об изменении количества движения системы в интегральной форме:

где 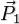и 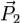— значения количества движения системы в моменты времени и 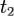соответственно, а 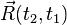— импульс внешних сил за промежуток времени 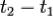. В соответствии со сказанным ранее и введёнными обозначениями выполняется

ВОПРОС 6

Запишем дифференциальное уравнение движения материальной точки в виде d(mV) / dt = F. Векторно умножим слева обе части уравнения на радиусвектор r, определяющий положение точки относительно неподвижного центра O, являющегося началом инерциальной системы координат, которую считаем неподвижной:

(1)

где правая часть r F = mO(F) является моментом силы относительно центра O. Дифференцируя по времени произведение R mV, находим левую часть

(1):

где V mV = 0, так как векторы V и mV параллельны. Подставляя правую и левую части в (1), получаем математическую запись теоремы об изменении момента количества движения материальной точки в дифференциальной форме:

(2)

По аналогии с моментом силы относительно центра векторное произведение в правой части (2) называют вектором моментом или просто моментом количества движения точки относительно центра O и обозначают kO, то есть

(3)

Из (3) следует, что вектор момент количества движения является векторной мерой движения точки вокруг центра O, так как он определяет линию действия количества движения точки. Действительно (рис. 32): вопервых, он перпендикулярен плоскости, где лежат центр и вектор количества движения точки, а его конец показывает верх этой плоскости; во-вторых, зная величину момента количества движения, всегда можно определить кратчайшее расстояние от центра до линии действия силы h = kO / mV.

Таким образом, по математической записи (2) мы можем сформулировать теорему об изменении момента количества движения в дифференциальной форме: производная по времени от момента количества

движения материальной точки относительно неподвижного центра равна моменту всех сил, приложенных к точке, относительно того же центра.

Естественно, что момент количества движения относительно центра обладает всеми свойствами момента силы относительно центра. В частности, он зависит от выбора центра, то есть является связанным вектором. Его проекция на ось, проходящую через центр, равна моменту вектора количества движения точки относительно той же оси. При вычислении момента количества движения можно применять теорему Вариньона.

Используя связь между векторами моментами количества движения и силы и их проекциями на оси координат, спроектируем (2) на оси инерциальной системы координат Oxyz и получим запись теоремы при

движении точки вокруг координатных осей:

(4)

где

моменты количества движения точки относительно координатных осей. Очевидно, что для вычисления моментов количеств движения относительно координатных осей можно использовать все свойства и приемы вычисления моментов сил, приложенных к точке, относительно осей координат - mx(F), my(F), mz(F).

Можно вывести эту теорему и в интегральной форме. Однако при этом нужно интегрировать правые части (2) и (4), это возможно, когда радиус-вектор r и координаты точки x, y, z известны как функции времени (их знание нужно для вычисления моментов сил), но тогда вообще отпадает надобность применения теоремы в интегральной форме.

Теорема имеет закон сохранения при движении вокруг центра, когда mO(F) = 0, а из (2) следует, что kO = r mV = const.

Закон сохранения может иметь место и при движении вокруг одной координатной оси, например оси Oz, когда mz(F) = 0, а из (4) следует, что kz = (r mV)z = const.

ВОПРОС 7

Для доказательства теоремы запишем дифференциальное уравнение движения точки в виде mdV / dt = F. Умножая обе части уравнения скалярно на вектор элементарного действительного перемещения точки dr и учитывая, что dr / dt = V, имеем

(1)

Зная, что F - равнодействующая сил, приложенных к точке, обозначим δA скалярное произведение в правой части и назовем его элементарной работой сил, приложенных к точке:

(2)

Находя дифференциал от mV2 / 2, имеем

Подставляя последнее выражение и выражение (2) в уравнение (1), получаем математическую запись теоремы в дифференциальной форме:

(3)

Половину произведения массы точки на квадрат ее скорости под знаком дифференциала в левой части уравнения (3) называют кинетической энергией точки.

Это замечание позволяет по математической записи сформулировать теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал от кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.

Отметим, что кинетическая энергия - это еще одна, но уже скалярная, мера движения материальной точки, что дает ей определенные преимущества перед векторными мерами движения - количеством движения и моментом количества движения. В системе СИ единицей измерения кинетической энергии является джоуль, 1 Дж = кг·(м2/с2) = (кг·м/c2)·м = 1 Н·м.

Предположим, что при переходе точки из начального положения M0 в конечное (или текущее) положение M ее скорость изменилась от начального значения V0 до текущего (или конечного) значения V, и при этих предположениях проинтегрируем выражение (3). Тогда

Интеграл в правой части этого выражения обозначим A и назовем полной работой или просто работой сил, приложенных к материальной точке:

(4)

Учитывая введенное обозначение, получаем математическую запись теоремы об изменении кинетической энергии материальной точки в интегральной форме:

mV2 / 2 - mV02 / 2 = A

(5)

то есть: изменение кинетической энергии материальной точки при ее переходе из начального положения в текущее (или конечное) положение

равна работе сил, приложенных к точке, совершенной при этом переходе.

ВОПРОС 8

Голономная система — механическая система, все механические связи которой можно свести к геометрическим (то есть, к голономным). Такие связи сводятся к ограничениям

только на положения тел системы. Уравнения связи 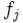записывают в виде:

где — координаты, 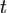— время, 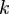— число связей.

Если все кинематические связи системы невозможно свести к геометрическим связям или их уравнения связи не могут быть проинтегрированы, то данная система будет неголономной.

Решение задач механики для голономных систем как правило проще, поскольку при этом можно воспользоваться многими разработанными методами и теоремами, например, уравнением Лагранжа, уравнением Гамильтона, уравнением Гамильтона-Якоби и др.

Пример[править | править исходный текст]

Математический маятник

Рассмотрим математический маятник, состоящий из точечной массы, подвешенной на нити в поле сил тяжести. Если считать, что длина нити не изменяется, то уравнение связи можно записать в виде:

где

— координаты массы

— длина нити.

Уравнение связи можно проинтегрировать, и как видно, оно не зависит от производных и 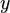, поэтому данная система — голономная.

Об этих новых понятиях уже говорилось в разделе “Кинематика”. Повторим их определение.

Вмеханике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела (а вместе с их производными по времени — соответствующими скоростями - полностью определяющая состояние механической системы или тела - то есть их положение и движение). Это фундаментальное понятие применяется в теоретической механике, теории механизмов и машин,машиностроении, авиации и теории летательных аппаратов, робототехнике и других областях.

Вотличие от обычных декартовых или какого-то другого типа координат, такие координаты в общем случае называются обобщёнными координатами (декартовы, полярные или какие-то другие конкретные координаты являются, таким образом, частным случаем обобщённых). По сути речь идет о минимальном наборе чисел, который полностью определяет текущее положение (конфигурацию) данной системы.

Требование минимальности этого набора или независимости координат означает, что подразумевается набор координат, необходимый для описания положения системы лишь при возможных движениях (например, если рассматривается математический маятник, подразумевается, что его длина не может меняться, и таким образом координата, которая характеризует расстояние от груза до точки подвеса не является его степенью свободы, т.к. не может меняться - то есть количество степеней свободы математического маятника в пространстве 2, а такого же маятника, который может двигаться только в одной плоскости, 1; им соответствуют углы отклонения маятника от вертикали).

В случае, когда рассматривается система со связями (точнее говоря, с удерживающими связями), количество степеней свободы механической системы меньше, чем количество декартовых координат всех материальных точек системы, а именно:

где n - количество степеней свободы, N - количество материальных точек системы, nlink - количество удерживающих связей за исключением избыточных[1].

ВОПРОС 9

“принцип возможных перемещений”.

Этот принцип считается наиболее общим условием равновесия или равномерного движения любой механической системы. Из него можно получить все аналитические условия равновесия тела под действием системы сил, рассматриваемые в разделе “Статика”.

Формулируется принцип следующим образом:

Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы была равна нулю.