Лекция № 2. Математическая модель сигналов

2.1. Математическое описание сигнала

Математическое описание и представление сигналов позволяет создать математическую модель сигнала.

Математическим описанием детерминированного сигнала служит детерминированная функция времени S(t). Это означает, что любому моменту времени ti соответствует определенное значение функции S(ti).

Математическое описание случайных (или нерегулярных) сигналов осуществляется с помощью случайных функций.

Случайными сигналами являются, например, напряжения или токи, соответствующие речи, музыке, последовательности телеграфных знаков и т.п. Для случайной функции ее значение при фиксированном аргументе ti – случайная величина.

В электросвязи находят применение гармонические и импульсные сигналы.

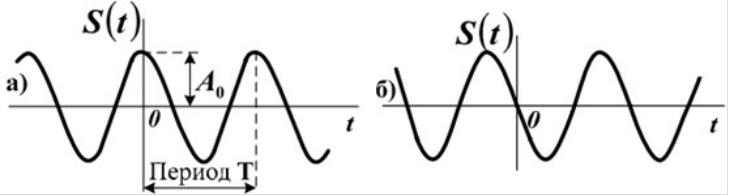
Гармонический сигнал (рис. 2.1), записывается в виде:

S(t) = A0cos(ωt + φ0),

(2.1)

где A0 – максимальное значение (амплитуда);

ω = 2πf – угловая частота;

f = 1/T – циклическая частота; φ0 = 2πτи/T– начальная фаза.

Рис. 2.1. Гармонический сигнал

На рисунке представлены гармонические сигналы с различными значениями начальной фазы (сдвиг 90о).

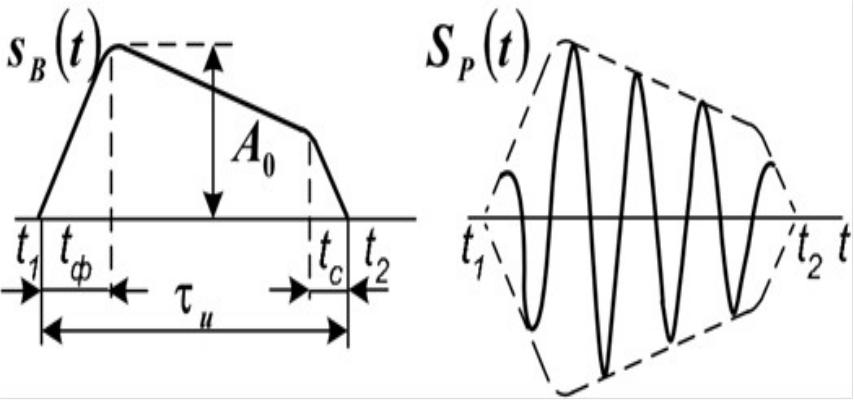
Импульсными являются сигналы, отличные от нуля в течение ограниченного времени. Эти сигналы существуют лишь в пределах конечного отрезка (t1, t2).

При этом различают видеоимпульсы (рис. 2.2, а) и радиоимпульсы (рис. 2.2, б).

Если sB(t) – видеоимпульс, то соответствующий ему радиоимпульс описывается выражением: SP(t) = sB(t) cos(ωt + φ0) (частота ω и начальная фаза φ0 могут быть произвольными).

В радиоимпульсе sB(t) называется огибающей, а функция cos(ωt + φ0) – заполнением.

Параметрами видеоимпульса принято считать его амплитуду A0, длительность τи, длительность фронта tф, длительность спада tc.

Происхождение термина «видеоимпульс» связано с тем, что впервые такие импульсы начали применять для описания сигналов в телевидении.

В электросвязи наибольшее применение находят одиночные импульсы или периодические последовательности импульсов, форма которых приближается к прямоугольной.

Для периодической последовательности импульсов, вводится понятие скважности, определяемой как отношение периода к длительности импульса: Q = T/ τи, T – период (временной интервал), так что S(ti + kT) =

S(ti), k = 0, ±1, ±2, …

Рис. 2.2. Импульсные сигналы: а) видеоимпульс; б) радиоимпульс

2.2. Математическое представление сигналов

Многие задачи теории связи и радиотехники, например вычисление отклика физической системы на известное входное воздействие, требуют специфической формы представления сигналов.

Способ получения таких моделей сигналов состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени.

Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно, в пределе будет получено точное представление исходного сигнала.

В литературе этот способ описания сигнала получил название динамического представления, подчеркивая развивающийся во времени процесс.

Широкое применение нашли два способа динамического представления. Согласно первому из них в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени ∆.

В качестве таких функций используются функции включения (рис. 2.3.) или функции Хевисайда σ(t), которые описываются следующим образом

Рис. 2.3. Функция включения

Другая возможность представления сигнала заключается в использовании стандартных прямоугольных функций длительностью ∆. На рис. 2.4 представлены возможные способы представления сигналов.

Рис. 2.4. Динамическое представление сигналов

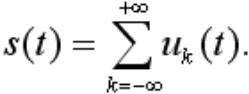
Как видно (рис. 2.4, а), текущее значение сигнала при любом t равно сумме ступенчатых функций

s(t) ≈ s0 σ(t) + (s1 - s0 )σ(t - Δ) + (s2 - s1 ) σ(t - 2Δ) + ···· (2.2)

В случае представления аналогового сигнала суммой примыкающих к друг другу прямоугольных импульсов, элементарный импульс с номером k представляется в виде

uk(t) = sk[σ(t - tk ) - σ(t - tk - Δ)].

(2.3)

Тогда исходный сигнал является суммой элементарных импульсов

(2.4)

Важное значение при динамическом представлении сигнала играет и другая функция, которая называется дельта-функцией δ(t) или функцией Дирака.

Такой функцией называется импульсный сигнал, площадь которого Am·τ равна 1, причем длительность импульса τ стремится к нулю, а

амплитуда импульса Am стремится к бесконечности.

Если в выражении (2.4) устремить к нулю, то получим формулу динамического представления сигнала

(2.5)

Таким образом, если непрерывную функцию умножить на дельта функцию и произведение проинтегрировать по времени, то результат будет равен значению функции в той точке, где существует δ-функция. В этом заключается фильтрующее свойство дельта-функции.

2.3. Геометрическое представление сигналов

Идеи функционального анализа дали возможность создать теорию сигналов, в основе которой лежит представление сигнала как вектора в некотором бесконечномерном пространстве.

Если имеется некая совокупность сигналов s1(t), s2(t) и т. д., имеющих

некоторые общие свойства, то их можно объединить в некоторое множество сигналов М = {s1(t), s2(t), …}.

Задача разложения сигнала сложной формы на простейшие составляющие сходна с разложением обычного вектора х трехмерного пространства на его составляющие по координатному базису единичных ортогональных векторов i, j, k. Такое представление можно записать как

x = х1i + х2 j + x3k

(2.6)

Составляющими вектора х по базису (i, j, k) будут векторы х1·i, х2·j, x3·k. Коэффициенты х1, х2, х3 представляют собой проекции вектора х на

координатные оси i, j, k и называются координатами вектора х. Иначе говоря, вектор х в трехмерном пространстве полностью определяется совокупностью его координат х = (х1, х2, х3).

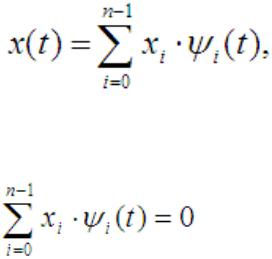
Чтобы перейти к обобщению понятия вектора трехмерного пространства для случая n-мерного пространства, функцию x(t) по аналогии с (2.6) можно представить в виде суммы

	(2.7)
где ψi – элементарные базисные функции.
Множество векторов	{ψ } называется линейно независимым
(базисом), если условие	выполняется лишь тогда, когда

все хi = 0.

Линейно независимые векторы {ψi} можно рассматривать как координатные оси пространства.

Метрическим называется линейное пространство, в котором определено расстояние между элементами (векторами) пространства (метрика), т.е. каждой паре элементов, скажем, х и у может быть поставлено в соответствие некоторое вещественное неотрицательное число d(х, у) и способ, в соответствии с которым находится это число.