Lineinaya_algebra_i_analiticheskaya_geometriya

31

Пример 17. Выяснить, являются ли линейно зависимыми векторы a 1,4, 2,3 и b 2,8, 4,6 .

Решение. Определим, пропорциональны ли координаты векторов:

14 2 3 – верно.

28 4 6

Следовательно, векторы a и b линейно зависимы.

Теорема 9. (Критерий линейной зависимости (независимости) системы из n век-

торов в пространстве Rn ).

Системы векторов a1 , a 2 , , a n – линейно зависима (линейно независима) в

Rn тогда и только тогда, когда определитель, составленный из координат этих векторов, равен нулю (отличен от нуля).

Пример 18. Определить, являются ли линейно зависимыми вектора

a 3, 2,1 ,

b 4,1, 3

и

c 2, 3, 1 ?

Решение. Составим и вычислим определитель из координат векторов:

3	2	1
4	1	3 3 1 9 2 4 6 1 12 2 40
2	3	1
Т.к. 0, то векторы a , b			и c - линейно независимы. 

Теорема 10. Любые n 1 векторов линейно зависимы в пространстве Rn .

Замечание. Остается рассмотреть ситуацию, когда количество векторов в систе-

ме больше двух, но меньше n (например, три вектора в пространстве R4 ). Итак, выясним линейную зависимость (независимость) системы a1 , a2 , , ak в простран-

стве Rn , где 2 k n . Рассмотрим матрицу A, составленную из координат этих векторов, и вычислим ее ранг. С учетом теоремы 5, делаем вывод: если rang A k ,

то система линейно независима, а если rang A k , то система a1 , a2 , , ak - ли-

нейно зависима.

32

1.6.2. Базисы в пространствах Rn .

Система векторов {e1 , e2 , , en } называется базисом пространства Rn , если

любой вектор a Rn может быть единственным образом представлен в виде линейной комбинации векторов этой системы:

a 1e1 2e2 nen .

Числа 1, 2 , , n называют коэффициентами разложения вектора a по базису

{e1 , e2 , , en } .

В пространстве R2 примером базиса может служить система единичных ортов: i , j . Данный базис принято называть естественным, т.к. коэффициентами

разложения любого вектора a по базису i , j являются координаты этого вектора. Например, a 2,5 2i 5 j .

В пространстве R3 естественный базис образует система векторов i , j,k .

Теорема 11. Если система векторов образуют базис в Rn , то она линейно независима.

Теорема 12. Любые n линейно независимых векторов пространства Rn образуют в нем базис.

Пример 19. (Образец решения задачи 3 из контрольной работы). Даны векторы

a 2, 1,2 , b 3,1, 1 ,	c 1, 2, 3 . Определить образуют ли векторы a , b			и
c базис в пространстве	R3 и если да,	то разложить вектор d 17, 15, 7		по
этому базису.
Решение. Составим определитель из векторов a , b и c :
	2	1	2
	3	1	1 10
	1	2	3

Т.к. 0, то система	a,b ,c - линейно независима и по теореме 12 образует
базис в пространстве R3 .	Значит, вектор d может быть единственным образом
представлен в виде:
	d x a y b z c

с пока неизвестными коэффициентами x, y, z. Переходя от равенства векторов к равенству их соответствующих координатприходим к системе линейных уравнений:

17				2			3			1
	15									2
			x	1		y	1		z			,
	7			2			1			3

33

откуда:

2x 3y z 17x y 2z 15.

2x y 3z 7

Решая эту систему, например, методом Крамера (сделайте это самостоятельно), получим: x 3, y 2 , z 5. Следовательно,

d 3a 2b 5c .

1.6.3. Скалярное произведение векторов. Норма вектора

Скалярным произведением вектора a (a1, a2 , , an ) на вектор b (b1,b2 , ,bn )

называется число

a b a1 b1 a2 b2 an bn .

Свойства скалярного произведения

Для любых a , b , c Rn и для любого числа справедливо:

1.a b b a ;

2.a b a b ;

3.a b c a b a c ;

4.a a 0 , причем a a 0 a 0 .

Нормой вектора a Rn называется арифметический корень из скалярного произведения вектора a на себя:

aa a a12 a22 an2 .

С геометрической точки зрения, норма вектора – это его длина.

Свойства нормы

Для любых a , b и для любого числа справедливо:

1.a 0, причем a 0 a 0 ;

2. aa;

3.a bab - неравенство Коши-Буняковского;

4.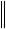a bab - неравенство треугольника;

Углом между векторами a и b называется число 0, , определяемое равенством:

34

cos aabb .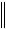

Откуда следует , что:

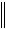a b ab cos ,

т.е. скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними. В этом состоит геометрический смысл скалярного произведения.

Векторы a и b называются ортогональными (перпендикулярными), если угол между ними 2 . Значит,

a b a b 0.

Пример 20. При каком значении x векторы a 2,3, x и b x, 1,5 ортогональны?

Решение.

a b a b 0,

т.е.

2x 3 5x 0 7x 3 x 73.

Ответ: a b при x 73 .

1.6.4. Векторное произведение векторов

Векторным произведением вектора a на вектор b называется вектор c , удовлетворяющий трем условиям (рис. 1):

1)c a , c b ;

2)длина вектора c численно равна площади параллелограмма, построенного

на векторах a и b ;

3) векторы a , b и c образуют правую тройку, т.е. если смотреть из конца вектора c , то кратчайший поворот от вектора a к вектору b должен происходить против часовой стрелки.

Свойства векторного произведения

Для любых векторов для любых a , b , c и для любого числа справедливо:

1.a b b a ;

2.a b a b ;

3.a b c a b a c ;

4.ab a b 0 ;

35

c

				b
				Рис. 1
		a
5. Таблица умножения ортов:
	i j k ,	j k i ,		k i j,
	j i k ,	k j i ,		i k j,
	i i 0,	j j 0,		k k 0.

6. Если a a1,a2 , a3 , b b1,b2 ,b3 , то

i j k

a b a1 a2 a3 . b1 b2 b3

Векторное произведение часто используют для нахождения площадей.

Пример 21. Найти площадь треугольника с вершинами A 5, 1,2 , B 3, 4, 2 , C 2,3,5 .

Решение. Найдем координаты векторов AB и AC (напомним, что для этого нужно из координат конца вектора вычестькоординаты начала):

AB ( 2; 3; 4) , AC ( 7;4;3)

B

A

Рис. 2

C

Учитывая, что норма векторного произведения векторов AB и AC численно равна площади параллелограмма, построенного на этих векторах (рис. 2), для нахождения площади треугольника достаточно будет площадь параллелограмма разделить на два.

36

AB AC S ABC 2 ,

	i	j	k	7i 34 j 29k 7,34, 29 .
AB AC	2	3	4
	7	4	3

AB AC72 342 29 2 2046

Таким образом, S 20462 .

1.6.5. Смешанное произведение векторов

Смешанным произведением векторов a , b и c (в указанном порядке) называется скалярное произведение векторного произведения первых двух векторов на третий:

ab c a b c.

Свойства смешанного произведения векторов

Для любых векторов a , b и c справедливо:

1)При перестановке местами двух множителей смешанное произведение меняет знак:

b ac ab c ,

acb ab c ,

cb a ab c

2) При циклической перестановке множителей смешанное произведение не меняется:

ab c b ca cab .

3) Если a a1,a2 , a3 , b b1,b2 ,b3 , c c1,c2 ,c3 , то

a1	a2	a3
ab c b1	b2	b3 .
c1	c2	c3

4) ab c 0 a , b и c компланарны, т.е. лежат в одной плоскости.

5) Абсолютная величина смешанного произведения векторов равна объему параллелепипеда, построенного на этих векторах

Vпарал. ab c .

Объем пирамиды, построенный на тех же векторах в 6 раз меньше:

37

Vпирам. 16 ab c .

Таким образом, скалярное произведение используют для нахождения длин и углов, векторное произведение – для вычисления площадей, а смешанное – для нахождения объемов.

Пример 22.(Образец выполнения задачи 4 из контрольной работы). Даны вершины пирамиды: A 4,1, 3 , B 2, 5,1 , C 3,4,3 и D 5,2, 4 .

Найти:
			D
a) длину ребра BD ;
b) угол между ребрами AB и AC ;
c) площадь грани BCD ;
d) объем пирамиды.
Решение.		A		B
a) Найдем вектор	BD , а затем его норму. Это
и будет длина	ребра BD . BD (3,7, 5) ,
BD 32 72 5 2 83			C
				Рис. 3

b) Угол между ребрами AB и AC будем находить как угол между векторами AB и AC (рис. 3), используя формулу:

			cos			AB AC .
					AB AC
		AB (6; 6;4),				AC (7;3;6),
		6 7 6 3 4 6					48	4	48	12
	cos	36 36 16			49 9 36		88 94		517	517 .
Следовательно, arccos			12 .
			517
c) S BCD	BC BD	, BC (1,9,2) ,			BD (3,7, 5)
	2
		i	j		k
	BC BD 1		9		2 59i 11j 20k 59,11, 20
		3	7	5
	BC BD 59 2			112 20 2			4002 , S BCD			4002 .
										2

d) Возьмем три вектора, на которых построена пирамида, например, AB (6, 6,4) , AC (7,3,6) и AD (9,1, 1), и найдем их смешанное произведение:

					38
					6	6	4
			AB AC AD 7			3	6	500.
					9	1	1
Значит, V		1	AB AC AD	1	500	250	.
пирам.		6		6		3

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Проверить линейную зависимость (независимость) векторов

1.a 1;3 , b 2; 6

2.a 1;5 , b 0;2

3.a 1;4;3 , b 0;7;2

4.a 5;2; 1;4 , b 10; 4;2; 8

5.a 1; 1;2 , b 0;3;5 , c 1;2;10

6.a 2;3; 1 , b 4; 1;2 , c 7;1;8

7.a 1;2;0; 1 , b 4; 1;3;2 , c 5;1;3;1

8.a 1;3;1;0 , b 2;1;4; 2 , c 3; 1;0;5

Доказать, что векторы a,b образуют базис в R2 и разложить по этому вектор c

9.a 1; 2 ,b 3;1 , c 7; 7

10.a 2; 1 ,b 1;1 , c 4; 1

Доказать, что векторы a,b ,c образуют базис в R3 и разложить по этому базису вектор d

11.a 3;0;2 , b 1; 1; 2 , c 2;1;2 , d 3; 3; 4

12.a 1;1;2 , b 2;0;2 , c 3; 1;1 , d 6;4;4

Найти внутренние углы и длины всех сторон ABC

13.A 1;0;1 , B 4; 1;2 , C 7;4;3

14.A 1;2;0 , B 3;2;1 , C 4;3;5

Определить при каком x векторы a и b ортогональны

15.a 1;2; x , b 2 x;3;7

16.a xi 3 j 2k , b i 2 j xk

17.Найти площадь параллелограмма, построенного на векторах

39

a 4;1;2 и b 5; 1;1 .

18.Дан ABC : A 3;1; 2 , B 1;3;2 , C 4;5;4 . Найти площадь ABC и длину высоты, опущенной из вершины C .

19.Даны векторы a 2;1; 3 и b 1; 2; 1 . Найти 2a b a 3b .

20.Даны вершины пирамиды: A 4; 1;2 , B 1;3;2 , C 2;2;5 , D 3;0;1 . Найти площади всех граней.

21.Упростить i 2 j 3k i 2i j 3k i .

22.Упростить 3i 4 j k 2i j 2i 3 j .

23. Найти объем параллелепипеда, построенного на векторах a 2; 1;0 , b 3;2; 1 , c 2;4;2 .

24. Найти объем пирамиды с вершинами в точках A 2;1;3 ,	B 1; 2;1 ,
C 2;1;2 , D 4;2; 2 и длину высоты, опущенной из точки D .

25.Установить, лежат ли в одной плоскости точки A 1;1;0 , B 4;2;3 , C 1;2;5 ,

D 1;0;2 .

26.Найти вектор x , коллинеарный вектору a 4;2;4 и удовлетворяющий условию x a 180.

27. Даны векторы a 3; 1;5 , b 1;2; 3 . Найти вектор x , перпендикулярный

коси OZ и удовлетворяющий условиям: x a 9, x b 4.

28.Даны точки A 5;1; 2 , B 4; 2;3 , C 0;3;2 . Найти единичный вектор, ортогональный векторам AB и AC .

29.Вычислить длины диагоналей параллелограмма ABCD , если AB 2a b ,

AD a 3b , a 3, b 2 , a,b 3 .

30. Векторы a и b ортогональны. Зная, что a 3,

b 4 , найти

a b a b и 3a b a 2b .

40

1.7. Комплексные числа

Комплексные числа применяются, в частности, для решения квадратных уравнений. Так, оставаясь в области множества действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.

Комплексным числом называется выражение вида z x iy , где x и y - дей-

ствительные числа, i - мнимая единица.

Число x называется действительной частью числа z и обозначается Re z , а число y - мнимой частью числа z и обозначается Im z , т.е. x Re z , y Im z .

Действительное число x является частным случаем комплексного z x iy при y 0. Комплексные числа вида z x iy , не являющиеся действительными (т.е. при y 0), называются мнимыми, а при x 0, y 0, т.е. числа вида z iy - чисто мнимыми.

Числа z x iy и z x iy называются сопряженными. Два комплексных числа z1 z1 iy1 и z2 z2 iy2 называются равными, если равны их действитель-

ные и мнимые части, т.е. z1 z2 , если Re z1 Re z2 ,	Im z1 Im z2 . В частности
z 0 , если Re z 0 и Im z 0 .

Арифметические операции на множестве комплексных чисел определяются следующим образом:

1. Сложение (вычитание) комплексных чисел:

z1 z2 x1 x2 i y1 y2 .

2. Умножение комплексных чисел:

z1 z2 x1x2 y1 y2 i x1 y2 x2 y1 .

В частности, i2 0 i 1 0 i 1 0 1 i 0 0 1

3. Деление двух комплексных чисел:

					z1	x1x2 y1 y2 i x2 y1 x1 y2	, z 0
					z2	x22 y22
Пример 23.					Даны два комплексных числа z1 2 3i и			z2 3 5i . Найти	z1 z2 ,
z z	2	, z z	2	,	z1 .
1		1			z
					2

Решение.

z1 z2 2 3i 3 5i 2 3 3 5 5 2i , z1 z2 2 3i 3 5i 2 3 i 3 5 1 8i , z1 z2 2 3i 3 5i (2 3 3 5) i 2 5 3 3 21 i ,