attachments_04-10-2012_21-18-24 / репетиционные тесты с теорией для ТиП (050502)

.

Если же на , то . Поэтому площадь S соответствующей криволинейной трапеции выразится формулой

, или .

Если линия пересекает ось , то отрезок надо разбить на части, в пределах которых не меняет знака, и к каждой части применить соответствующую формулу.

Выражение вида , где – произвольные действительные числа, – мнимая единица, , т.е. , называется комплексным числом. При этом называется действительной частью (абсциссой), – мнимой частью (ординатой).

()

– это тригонометрическая форма комплексного числа.

– это показательная форма комплексного числа.

Формулы перехода:

Два комплексных числа и , действительные части которых равны, а мнимые противоположны по знаку, называются комплексно сопряжёнными числами.

Суммой (разностью) комплексных чисел и называют комплексное число вида

Произведение комплексных чисел определяется как произведение двучленов с применением обычного правила раскрытия скобок.

.

Чтобы отыскать частное , надо умножить числитель и знаменатель дроби на одно и то же число, сопряжённое знаменателю, т.е. число .

В тригонометрической форме:

,

,

,

Функция называется периодической, если существует такое число (период), что для любого х из области определения выполняется: . График периодической функции периодически повторяется.

1. Если функция имеет период , то она имеет период и , где .

2. Если функция имеет период , то функция имеет период .

Периоды тригонометрических функций: , имеют период , , – период .

Простейшим периодическим движением (процессом) является гармоническое колебание – это движение, характеризующееся определённой повторяемостью во времени, при котором колеблющаяся величина изменяется со временем по закону синуса или косинуса:

или .

Здесь:

– амплитуда колебания (максимальное значение колеблющейся величины);

– круговая (циклическая) частота (или угловая скорость, характеризующая быстроту колебания величины), ,

где – период гармонического колебания (наименьший промежуток времени, по истечению которого колеблющаяся величина снова возвращается в то же состояние, в котором она находилась в начальный произвольно выбранный момент);

– начальная фаза колебаний в момент времени ;

– фаза колебаний в момент времени .

Пусть – периодическая функция с периодом , определённая на отрезке , тогда она разложима в ряд Фурье на :

,

где , , , .

1) если функция на отрезке – чётная, то

, где , , , все .

2) если функция на отрезке – нечётная, то

, где , , все коэффициенты и .

Линейное однородное ДУ второго порядка с постоянными коэффициентами имеет вид: , где – постоянные действительные числа. Общее решение определяется с помощью характеристического уравнения: , которое имеет два корня и . Возможны три случая:

1) – действительные различные корни , тогда общее решение записывается в виде:

.

2) – действительные совпавшие корни , тогда общее решение имеет вид:

.

3) , – комплексно-сопряжённые корни, тогда общее решение имеет вид:

.

Общее решение линейного неоднородного ДУ второго порядка равно сумме общего решения соответствующего линейного однородного ДУ второго порядка и любого частного решения данного неоднородного ДУ:

.

Частное решение в некоторых случаях может быть найдено методом неопределённых коэффициентов.

I. Если правая часть имеет вид: , где – многочлен степени ,

• число не является корнем характеристического уравнения, то частное решение: ;

• число – простой корень характеристического уравнения (однократный), тогда ;

• число – двукратный корень характеристического уравнения, тогда .

Здесь – многочлен степени с неопределёнными коэффициентами.

II. Если правая часть имеет вид: ,

• числа не являются корнями характеристического уравнения, то частное решение ;

• числа являются корнями характеристического уравнения, то частное решение будем искать в виде: .

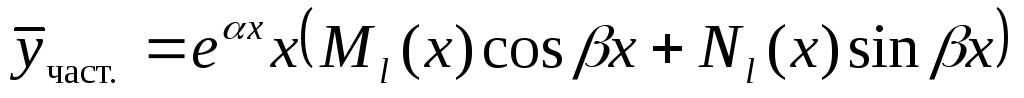Здесь , – многочлены степени с неопределёнными коэффициентами.

Вероятность наступления любого события заключается в пределах: .

Событие – невозможное , событие – достоверное .

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них, т. е. появление хотя бы одного из событий полной группы есть достоверное событие.

События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, иначе – В зависит от события А.

Суммой двух событий A и B называют событие , состоящее в появлении события А, или события В, или обоих этих событий.

В частности, если события А и В – несовместные, то А+В – событие, состоящее в появлении одного их этих событий, безразлично какого.

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий, т.е.

.

Произведением двух событий А и В называют событие , состоящее в совместном появлении (совмещении) этих событий.

Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий, т.е.

.

Условной вероятностью называется вероятность события В, вычисленная в предположении, что событие А уже наступило.

Теорема умножения вероятностей совместных событий. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило, т.е.

.

Теорема сложения вероятностей совместных событий. Вероятность появления одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления, т.е.

.

Пусть дискретная случайная величина (ДСВ) задана законом распределения:

где .

Математическое ожидание ДСВ равно .

Пусть из генеральной совокупности извлечена выборка объектов по некоторому признаку X, причём значения наблюдались соответственно раз и – объём выборки. Наблюдаемые значения называются вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений называются частотами, а их отношения к объёму выборки – относительными частотами. Сумма относительных частот равна единице.

Статистическим распределением выборки называют соответствие между вариантами и их частотами или относительными частотами.

Полигоном частот называется ломаная, отрезки которой соединяют точки , , …, . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты .

Числовые характеристики вариационного ряда:

Выборочной средней называют среднее арифметическое значение признака выборки.

Если все значения признака выборки объёма n различны, то .

Если же значения признака имеют соответственно частоты , причём , то .

Выборочной дисперсией D называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :

.

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии: .

Модой М называется варианта, которая имеет наибольшую частоту.

Медианой m называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечётно, т.е. , то , при чётном медиана равна .

Несмещённой оценкой генеральной средней (математического ожидания) служит выборочная средняя.

Длина вектора в евклидовом пространстве вычисляется по формуле

.

Векторы и , заданные в ортонормированном базисе своими координатами, взаимно перпендикулярны тогда и только тогда, когда

.

Два вектора и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:

.

Пусть дан график функции .

1) при график расположен выше оси ; 2) при график ниже оси .

1) при функция возрастает; 2) при функция убывает.

1) при функция выпуклая (); 2) при функция вогнутая ().

, .

Несобственный интеграл вида сходится при , расходится при .

Мера плоского множества есть площадь фигуры: .

Достаточное условие расходимости ряда

Если или этот предел не существует, то ряд расходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд , составленный из модулей членов данного ряда.

Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд , составленный из модулей его членов, расходится.

Признак Лейбница. Пусть дан знакочередующийся ряд .

Если члены ряда по абсолютной величине монотонно убывают: или