attachments_04-10-2012_21-18-24 / репетиционные тесты с теорией для ТиП (050502)

и , то этот ряд сходится, при этом его сумма удовлетворяет неравенствам .

1) , – геометрический ряд: при – сходится, при – расходится.

2) – гармонический ряд – расходится.

3) – обобщённый гармонический ряд: при сходится, при расходится.

Пусть – радиус сходимости степенного ряда . Множество точек : называется кругом сходимости степенного ряда, т.е. это интервал (концы этого интервала исследуются отдельно).

Выражение вида , где – произвольные действительные числа, – мнимая единица, , т.е. , называется комплексным числом. При этом называется действительной частью (абсциссой), – мнимой частью (ординатой).

– это тригонометрическая форма комплексного числа.

– это показательная форма комплексного числа.

Формулы перехода:

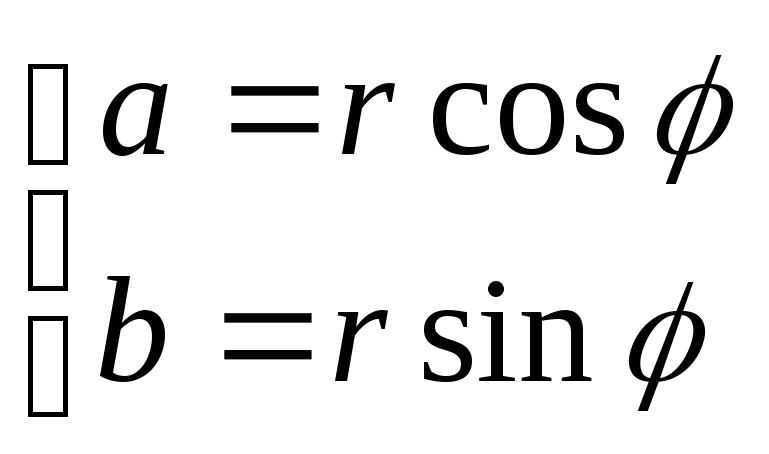
Два комплексных числа и , действительные части которых равны, а мнимые противоположны по знаку, называются комплексно сопряжёнными числами.

Суммой (разностью) комплексных чисел и называют комплексное число вида

Произведение комплексных чисел определяется как произведение двучленов с применением обычного правила раскрытия скобок.

Чтобы отыскать частное , надо умножить числитель и знаменатель дроби на одно и то же число, сопряженное знаменателю, т.е. число .

В тригонометрической форме:

,

,

,

Перевести комплексное число в тригонометрическую форму, т.е.

Функция называется периодической, если существует такое число (период), что для любого х из области определения выполняется: .

Периоды тригонометрических функций: , имеют период , , – период .

1. , , тогда ; 2. , , тогда ;

3. , , ; 4. , , .

График периодической функции периодически повторяется.

Пусть – периодическая функция с периодом , определённая на отрезке , тогда она разложима в ряд Фурье на :

, где

, , , .

1) если функция на отрезке – чётная, то

, где , , , все .

2) если функция на отрезке – нечётная, то

, где , , все .

ДУ второго порядка, допускающие понижение порядка:

1 случай. ДУ не содержит искомую функцию , замена: .

2 случай. ДУ не содержит переменную , замена: .

- это ДУ с разделяющимися переменными. , , , . Найдём значение постоянной из условия : , , . Тогда частное решение имеет вид: , т.е. . Значит, .

ДУ -го порядка вида . Общее решение находится последовательным интегрированием данного ДУ раз.

- это ДУ третьего порядка, интегрируем три раза:

, , .

Линейное однородное ДУ второго порядка с постоянными коэффициентами имеет вид: , где – постоянные действительные числа. Общее решение определяется с помощью характеристического уравнения: , которое имеет два корня и . Возможны три случая:

1) , тогда общее решение записывается в виде: .

2) , тогда общее решение имеет вид: .

3) , – комплексно-сопряжённые корни, тогда .

Общее решение линейного неоднородного ДУ второго порядка равно сумме общего решения соответствующего линейного однородного ДУ второго порядка и любого частного решения данного неоднородного ДУ:

.

Частное решение может быть найдено методом неопределённых коэффициентов.

I. Если правая часть имеет вид: , где – многочлен степени ,

• число не является корнем характеристического уравнения, то ;

• число – простой корень характеристического уравнения (однократный), то ;

• число – двукратный корень характеристического уравнения, то .

Здесь – многочлен степени с неопределёнными коэффициентами.

II. Если правая часть имеет вид: ,

• числа не являются корнями характер. уравнения, то ;

• числа 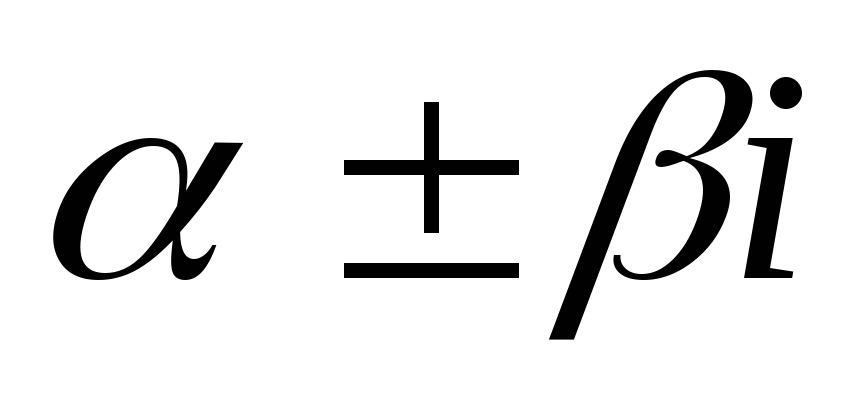являются корнями характер. уравнения, то .

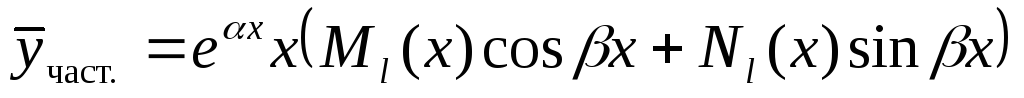Здесь , – многочлены степени с неопределёнными коэффициентами.

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, иначе – В зависит от события А.

Несовместные события , , … образуют полную группу, если в результате испытания появится хотя бы одно из них, т.е. появление хотя бы одного из событий полной группы есть достоверное событие, т.е.

.

Закон распределения непрерывной случайной величины задаётся с помощью так называемой плотности распределения вероятности. Вероятность того, что значение принятое непрерывной случайной величиной , попадает в промежуток , определяется равенством . График функции называется кривой распределения. Геометрическая вероятность попадания случайной величины в промежуток равна площади криволинейной трапеции, ограниченной кривой распределения, осью и прямыми , .

Свойства плотности распределения: 1. ; 2. .

У нас: , .

Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки .

У нас: , шаг , тогда , .

Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Выборочной средней называют среднее арифметическое значение признака выборки.

Если каждый элемент выборки изменить в раз, то выборочная средняя также изменится в раз, выборочная дисперсия – в раз, т.е. .

Размещением из n объектов по k называют любой выбор k объектов, взятых в определенном порядке из n объектов. Число размещений из n объектов по k обозначают: .

Размещения из n элементов по n называются перестановками:

Сочетаниями из n по k называют любой выбор k объектов, взятых из n объектов:

У нас:

Решение ДУ ищем в виде ряда Тейлора (Маклорена, т.к. ):

У нас: , найдём , для этого подставим и в исходное ДУ:

. Для нахождения коэффициента дифференцируем данное ДУ: , тогда

. Итак,

.

Формула нахождения приближённого значения функции по её значению : , где - бесконечно малая функция.

У нас: , тогда , , , , . Значит, .

26