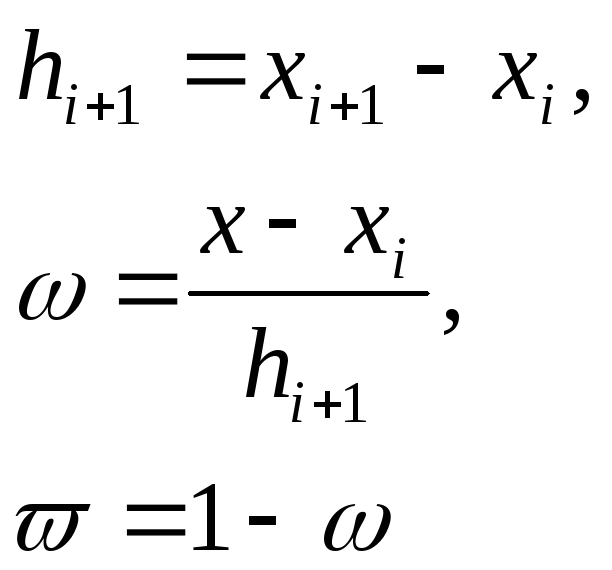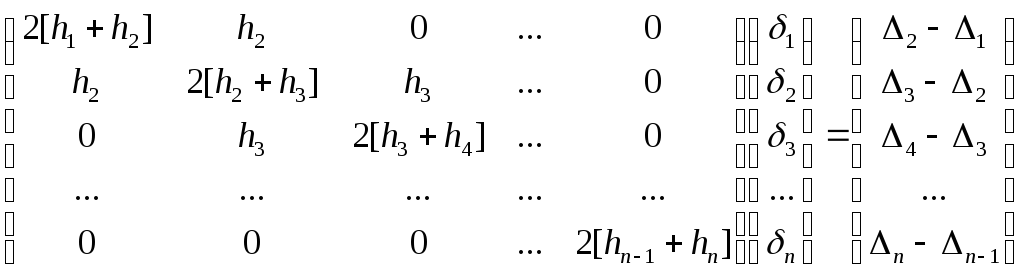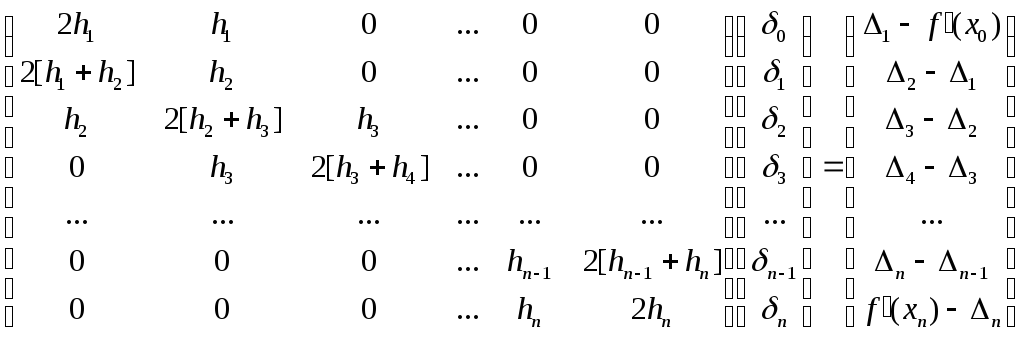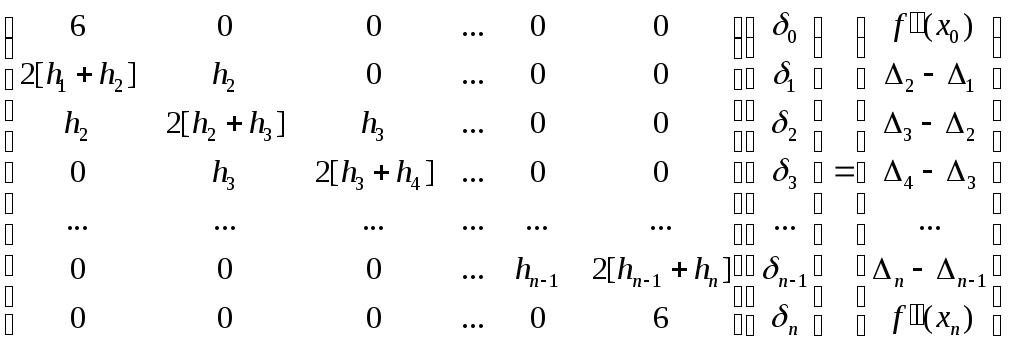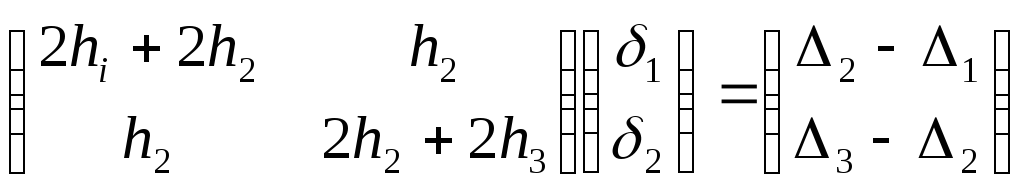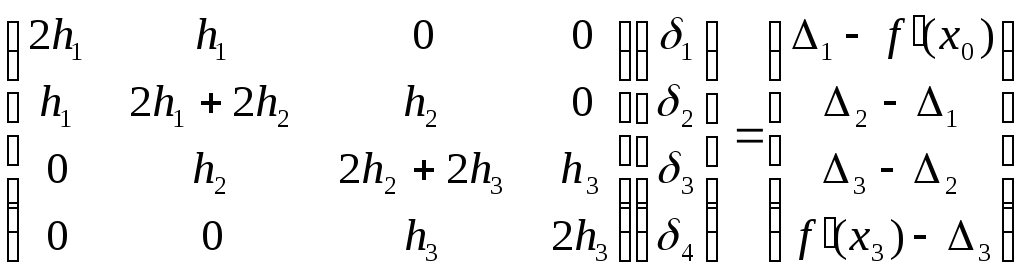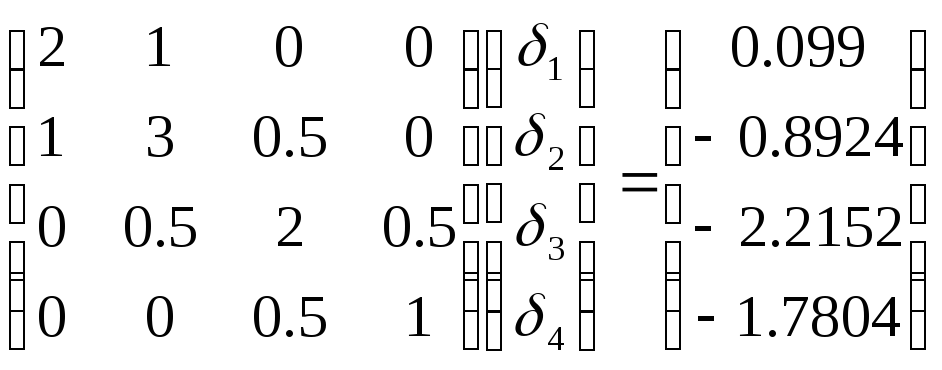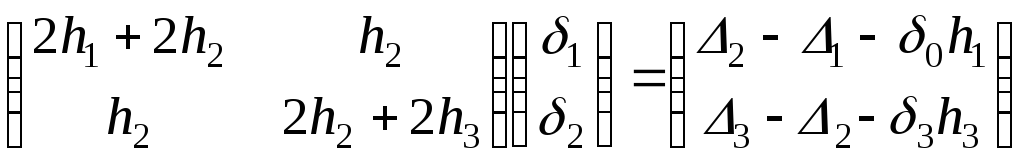МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
Институт радиоэлектроники и информационных технологий - РТФ
Кафедра Автоматика и информационные технологии
Интерполяция сплайнами
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К лабороторной работе ПО ДИСЦИПЛИНЕ «Численные методы»
|
2011 |
Составитель И.А.Селиванова, ст.преподаватель.
ИНТЕРПОЛЯЦИЯ СПЛАЙНАМИ: Методические указания к практическим занятиям по дисциплине «Численные методы»
Указания предназначены для студентов всех форм обучения направления 230100 – «Информатика и вычислительная техника».
Ó ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина», 2011
СОДЕРЖАНИЕ
1. ИНТЕРПОЛЯЦИЯ СПЛАЙНАМИ. 4
1.1. Кубические сплайны. 4
1.2. Специальная форма записи сплайна. 5
1.3. Квадратичные сплайны. 13
1.4. Задание на практику. 18
1.5. Варианты заданий. 19
Список литературы 21
1. Интерполяция сплайнами.
В случаях, когда промежуток [a,b], на котором требуется заменить функцию f(x) велик, можно применить интерполяцию сплайнами.
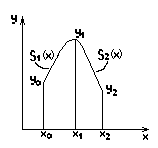
1.1. Кубические сплайны.
Интерполяционные сплайны 3-го порядка - это функции, состоящие из кусков многочленов 3-го порядка. В узлах сопряжения обеспечивается непрерывность функции, ее первой и второй производных. Аппроксимирующая функция составляется из отдельных многочленов, как правило, одинаково небольшой степени, определенных каждый на своей части отрезка [a,b].
Пусть
на отрезке [a,b]
вещественной оси x
задана
сетка
![]() ,
в узлах которой определены значения
,
в узлах которой определены значения![]() функцииf(x).
Требуется
построить на отрезке [a,b]
непрерывную функцию-сплайн S(x),
которая удовлетворяет следующим
условиям:
функцииf(x).
Требуется
построить на отрезке [a,b]
непрерывную функцию-сплайн S(x),
которая удовлетворяет следующим
условиям:
На каждом отрезке
 сплайн является многочленом
сплайн является многочленом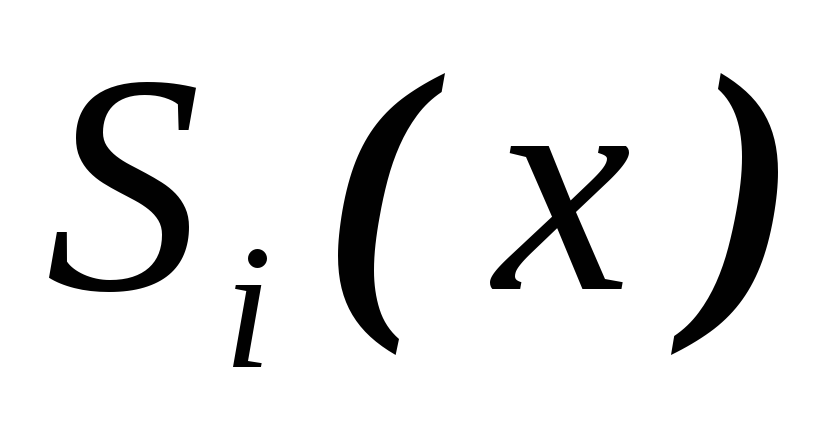 третьей степени:
третьей степени:
|
|
(1) |
В узлах
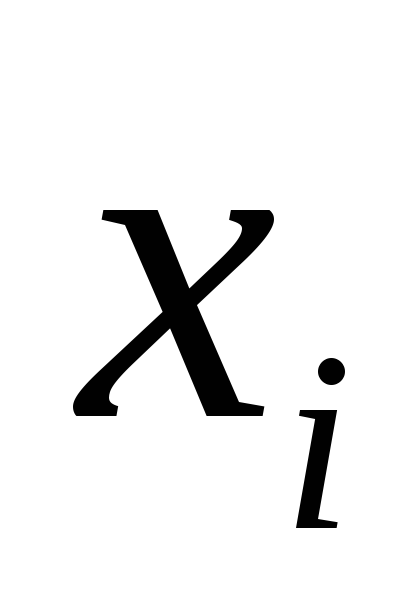 сплайн
сплайн принимает заданные значения
принимает заданные значения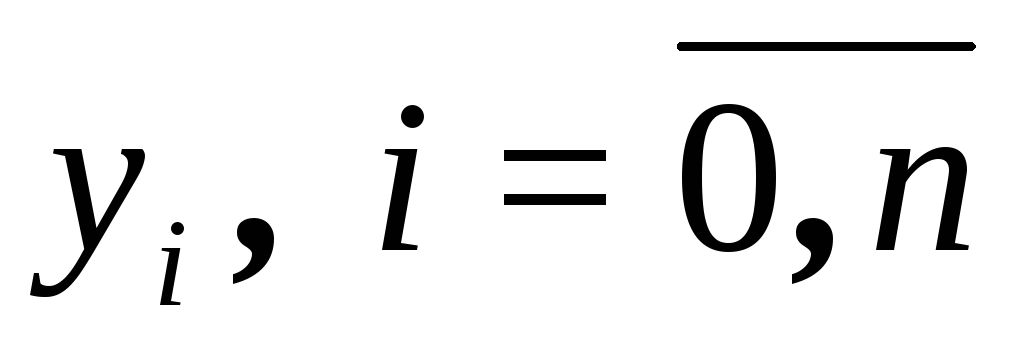 ,
т.е.
,
т.е.
|
|
(2) |
Во внутренних узлах
 сплайн имеет непрерывную первую и
вторую производные, т.е. в узлах сопряжения
сплайнов их первые и вторые производные
должны быть равны:
сплайн имеет непрерывную первую и
вторую производные, т.е. в узлах сопряжения
сплайнов их первые и вторые производные
должны быть равны:
|
|
(3) |
Для
построения искомого сплайна требуется
найти коэффициенты
![]() многочленов
многочленов![]() ,i=1,…n,
т.е. 4n
неизвестных
коэффициента, которые удовлетворяют
4n-2
уравнениям (1), (2), (3). Чтобы система
уравнений имела решение, добавляют еще
два дополнительных (краевых) условия.
Используется три типа краевых условий:
,i=1,…n,
т.е. 4n
неизвестных
коэффициента, которые удовлетворяют
4n-2
уравнениям (1), (2), (3). Чтобы система
уравнений имела решение, добавляют еще
два дополнительных (краевых) условия.
Используется три типа краевых условий:
I)
|
|
(4) |
Сплайн, определяемый (4) называется естественным кубическим сплайном.
II)
|
|
(5) |
III)
|
|
(6) |
Условия (1), (2), (3) и одно из условий (4), (5), (6) образуют СЛАУ порядка 4n. Решение системы можно провести с помощью метода Гаусса. Однако, выбрав специальную форму записи кубического многочлена, можно существенно снизить порядок решаемой системы уравнений.
1.2. Специальная форма записи сплайна.
Рассмотрим
отрезок
![]() .
Введем следующие обозначения переменных:
.
Введем следующие обозначения переменных:
|
|
(7) |
Здесь
![]() - длина отрезка
- длина отрезка
![]() ,
,
![]() ,
,
![]() -
вспомогательные переменные,
-
вспомогательные переменные,
x
– промежуточная точка на отрезке
![]() .
.
Когда
x
пробегает
все значения на интервале
![]() ,
переменная
,
переменная![]() изменяется от 0 до 1, а
изменяется от 0 до 1, а![]() изменяется от 1 до 0.
изменяется от 1 до 0.
Пусть
кубический многочлен
![]() на отрезке
на отрезке![]() имеет вид:
имеет вид:
|
|
(8) |
Номер
сплайна совпадает с индексом конечной
точки отрезка
![]() .
Для записи сплайна на соседнемi-ом
участке достаточно в (8) уменьшить все
индексы на единицу:
.
Для записи сплайна на соседнемi-ом
участке достаточно в (8) уменьшить все
индексы на единицу:
|
|
(3.9) |
Переменные
![]() и
и![]() определяются применительно к конкретному
отрезку интерполяции.
определяются применительно к конкретному
отрезку интерполяции.
Найдем
значение сплайна
![]() на концах отрезка
на концах отрезка![]() .
Точка
.
Точка![]() является начальной для отрезка
является начальной для отрезка![]() ,
поэтому
,
поэтому![]() =0,
=0,![]() =1
и в соответствии с (3.8):
=1
и в соответствии с (3.8):![]() .
.
На
конце отрезка
![]()
![]() =1,
=1,![]() =0
и
=0
и![]() .
.
Для
интервала
![]() точка
точка![]() является конечной, поэтому
является конечной, поэтому![]() =1,
=1,![]() =0
и из формулы (9) получаем:
=0
и из формулы (9) получаем:![]() .
Таким образом, выполняется условие
непрерывности функцииS(x)
в
узлах стыковки кубических многочленов
независимо от выбора чисел i
.
.
Таким образом, выполняется условие
непрерывности функцииS(x)
в
узлах стыковки кубических многочленов
независимо от выбора чисел i
.
Для определения коэффициентов i , i=0,…n продифференцируем (8) дважды как сложную функцию от x. Тогда
|
|
(10) |
где
|
|
(11) |
Уменьшая в (10) индекс i на единицу, получим:
|
|
(12) |
Определим
вторые производные сплайна
![]() и
и![]() :
:
|
|
(13) |
|
|
(14) |
Для
многочлена
![]() точка
точка![]() является началом отрезка интерполяции
и
является началом отрезка интерполяции
и![]() =0,
=0,![]() =1,
поэтому
=1,
поэтому
|
|
(15) |
Для
сплайна
![]() точка
точка![]() является концом отрезка интерполяции
и
является концом отрезка интерполяции
и![]() =1,
=1,![]() =0.
Отсюда
=0.
Отсюда
|
|
(16) |
Из (15) и (16) следует, что на отрезке [a,b]сплайн-функция, «склеенная» из кусков многочленов 3-го порядка, имеет непрерывную производную 2-го порядка.
Чтобы получить непрерывность первой производной функции S(x), потребуем во внутренних узлах интерполяции выполнения условия:
|
|
|
Определим
(10) и (12)
в точке
![]() :
:
![]()
Приравнивая полученные выражения, приходим к системе уравнений:
|
|
(17) |
Для
естественного кубического сплайна
![]() ,
следовательно, система уравнений будет
иметь вид:
,
следовательно, система уравнений будет
иметь вид:
|
|
(18) |
Решаемая
система уравнений является линейной,
а ее матрица трехдиагональной,
симметричной. Такая матрица является
невырожденной, и коэффициенты
![]() определяются из системы (18) однозначно.
определяются из системы (18) однозначно.
Если же требуется найти S(x) с краевыми условиями (3.5), то это приведет к дополнительным условиям:
|
|
|
и система уравнений (17) будет иметь вид:
|
|
(19) |
Для краевых условий (6) получим:
|
|
(20) |
и система уравнений (17) будет иметь вид:
|
|
(21) |
Пример.
Исходные данные:
|
i |
0 |
1 |
2 |
3 |
|
|
1 |
2 |
2.5 |
3 |
Заменить
функцию
![]() интерполяционным кубическим сплайном,
значения которого в заданных узловых
точках (см. табл.) совпадают со значениями
функции в этих же точках. Рассмотреть
разные краевые условия.
интерполяционным кубическим сплайном,
значения которого в заданных узловых
точках (см. табл.) совпадают со значениями
функции в этих же точках. Рассмотреть
разные краевые условия.
Рассчитаем значение функции в узловых точках. Для этого подставим в заданную функцию значения из таблицы.
![]()
![]()
![]()
![]()
![]()
Для разных краевых условий (4), (5), (6) найдем коэффициенты кубических сплайнов.
Рассмотрим первые краевые условия.
|
|
|
В
нашем случае n=3,
![]() ,
,![]() ,
,![]() .
Чтобы найти
.
Чтобы найти![]() используем систему уравнений (3.18):
используем систему уравнений (3.18):
|
|
|
Вычислим
![]() и
и![]() ,
используя формулы (7) и (11):
,
используя формулы (7) и (11):
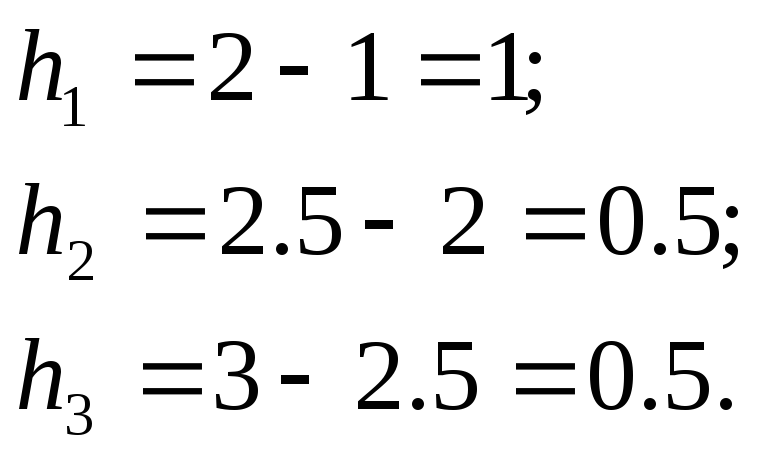
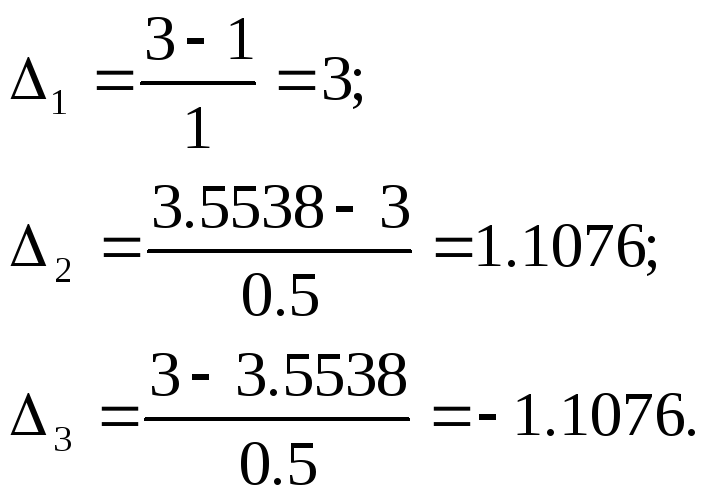
Подставим полученные значения в систему уравнений:
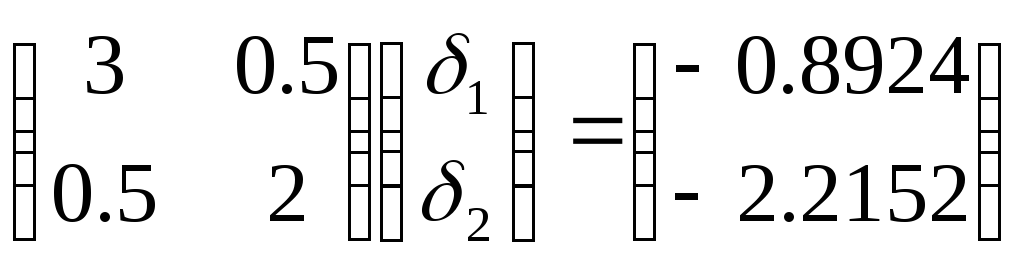 .
.
Решение системы:
![]()
С учетом первых краевых условий коэффициенты сплайна:
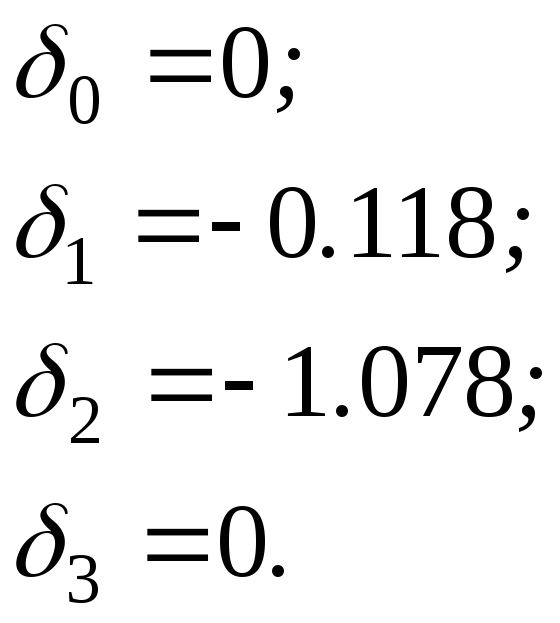
Рассмотрим определение коэффициентов сплайна с учетом краевых условий (3.5):
|
|
|
Для n=3 система уравнений (19) примет вид:
|
|
(21) |
Найдем
производную функции
![]() :
:
![]()
Вычислим
![]() и
и![]() :
:
![]()
Подставим
в систему уравнений (21) значения
![]() и
и![]() :
:
|
|
|
Решение системы уравнений:
|
|
|
Рассмотрим третьи краевые условия (6).
|
|
|
Используя формулу (20) определим 0 и 3:
|
|
|
Найдем
вторую производную функции
![]() :
:
|
|
|
Вычислим
![]() и
и![]() :
:
|
|
|
и
|
|
|
Система
уравнений (21)для определения
![]() ,
,![]() :
:
|
|
|
С учетом конкретных значений:
|
|
|
и вектор коэффициентов:
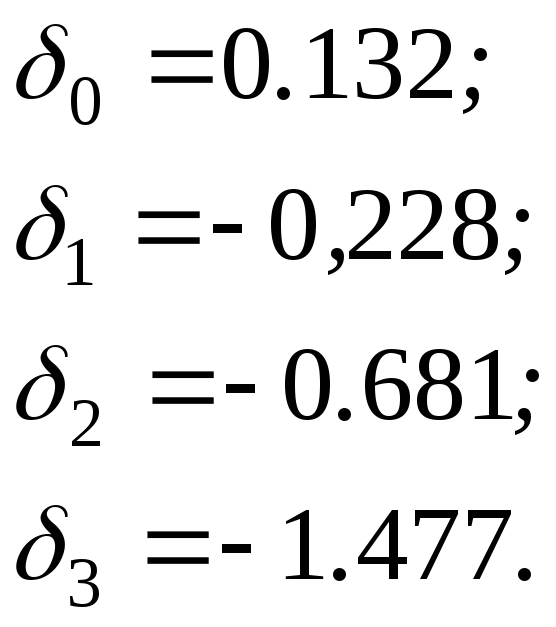
Рассчитаем значения кубического сплайна S(x) в серединах отрезков интерполяции.
Середины отрезков:
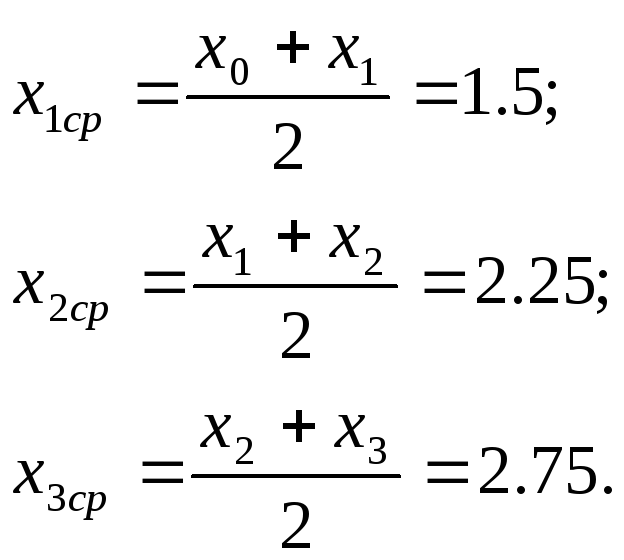
Для вычисления значения кубического сплайна в серединах отрезков интерполяции воспользуемся формулами (7) и (9).
3.1.
![]()
Найдем
![]() и
и![]() :
:
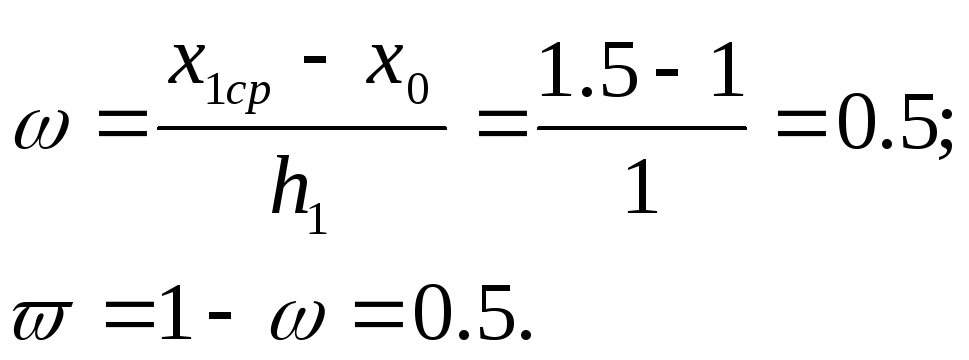
В
формулу (3.9) подставляем коэффициенты
![]() ,
для краевых условий (4), (5), (6):
,
для краевых условий (4), (5), (6):

![]()
3.2.
![]()
Найдем
![]() и
и![]() :
:
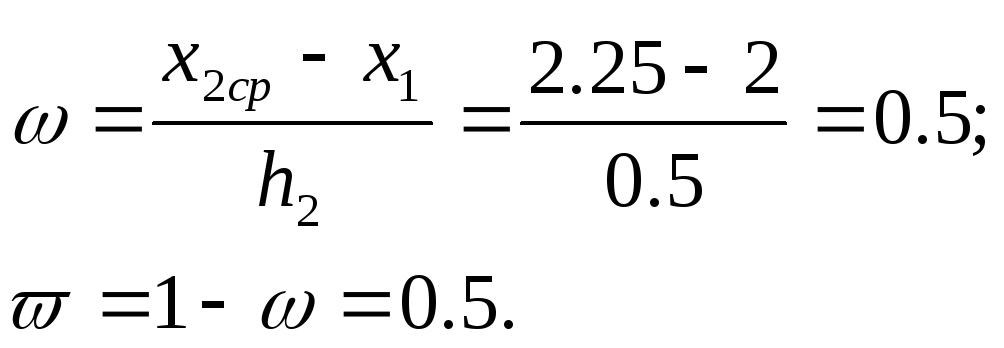
В
формулу (9) подставляем коэффициенты
![]() ,
для краевых условий (4), (5), (6):
,
для краевых условий (4), (5), (6):
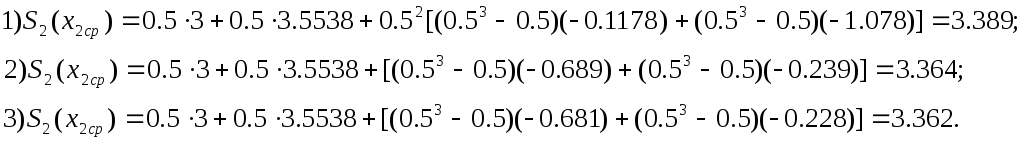
3.3.
![]()
Найдем
![]() и
и![]() :
:

В
формулу (9) подставляем коэффициенты
![]() ,
для краевых условий (4), (5), (6):
,
для краевых условий (4), (5), (6):
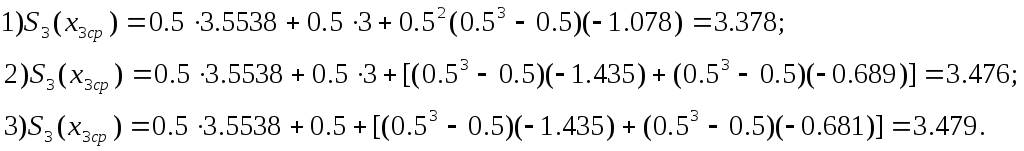
Составим таблицу:
|
|
|
|
|
f(x) |
|
|
2.044 |
2.026 |
2.026 |
|
|
|
3.389 |
3.364 |
3.362 |
|
|
|
3.378 |
3.476 |
3.479 |
|