Фазовые портреты НЛДС

54

При построении фазовых портретов в случае, когда система (5) не имеет положений равновесия, можно использовать следующие рекомендации:

1. Найти первый интеграл уравнения

		dx			dy
						,
		ax by			cx dy
	и таким образом определить семейство всех фазовых траекторий.
2.	Найти главные изоклины:		ax by 0 (ВИ), cx dy 0 (ГИ).
3.	Найти прямые, содержащие фазовые траектории, в виде у = kx + .
	При этом для нахождения коэффициентов k и , учитывая, что
		c : a d : b ,

построить уравнение:

	dy					(ax by)
k						ax by
	dx
				y kx

		.
	(a kb)x b
y kx

Фазовые портреты НЛДС

55

	Так как выражение
		(a kb)x b

не зависит от x, если a + kb = 0, то получим следующие условия для

нахождения k и :	a kb 0,	k .
		b

Уравнение прямой можно искать и в виде x = ky + . Условия для определения k и строятся аналогично.

Если существует только одна прямая, то она является асимптотой для остальных траекторий.

2.Для определения направления движения по фазовым траекториям определить области «знакопостоянства» правых частей системы (5).

3.Для определения характера выпуклости (вогнутости) фазовых траекторий построить производную y”(x) и установить области ее «знакопостоянства».

Различные приемы построения фазовых портретов рассмотрим на примерах.

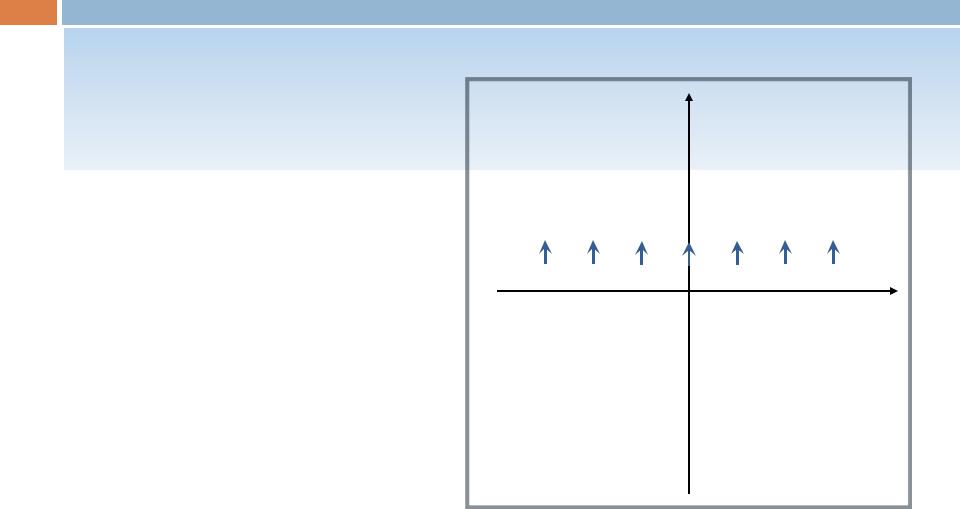
Пример 9.

56

dx

0,

y

dt

dy

1.

dt

Решив уравнение:

dx

0

0,

dy

1

получим, что все фазовые траек-

тории лежат на прямых

x

x C,

C R.

Так как y’(t)=1 > 0, то ордината

движущейся точки по любой

фазовой траектории возрастает.

Следовательно, движение по

фазовым траекториям происходит

снизу вверх.

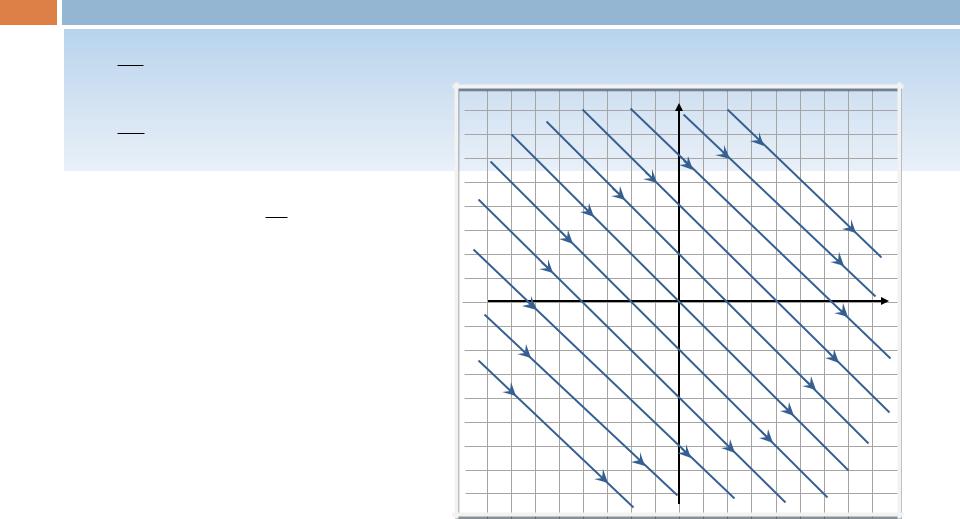
Пример 10.

57

dx	2,
dt		y
dy	2.
dt
	dy	2
Решив уравнение: dx		2 1,
получим, что все фазовые траек-
тории лежат на прямых		x
	y x + C, C R.
Так как y’(t) < 0, то ордината
движущейся точки по любой
фазовой траектории убывает.
Следовательно, движение по
фазовым траекториям происходит
сверху вниз.

Пример 11.

58

	dx			1,
	dt
	dy			x	1.
	dt
	Решив уравнение:					dy	x 1,
						dx

получим, что фазовыми траекториями системы являются параболы:

		(x 1)2
	y		C,	C R,
		2

оси которых лежат на горизонтальной изоклине x 1 0, а ветви направлены вверх.

Так как x’(t) 1 > 0, то абсцисса движущейся точки по любой фазовой траектории возрастает. Следовательно, движение по левой ветви параболы происходит сверху вниз до пересечения с прямой – горизонтальной изоклиной, а далее – снизу вверх.

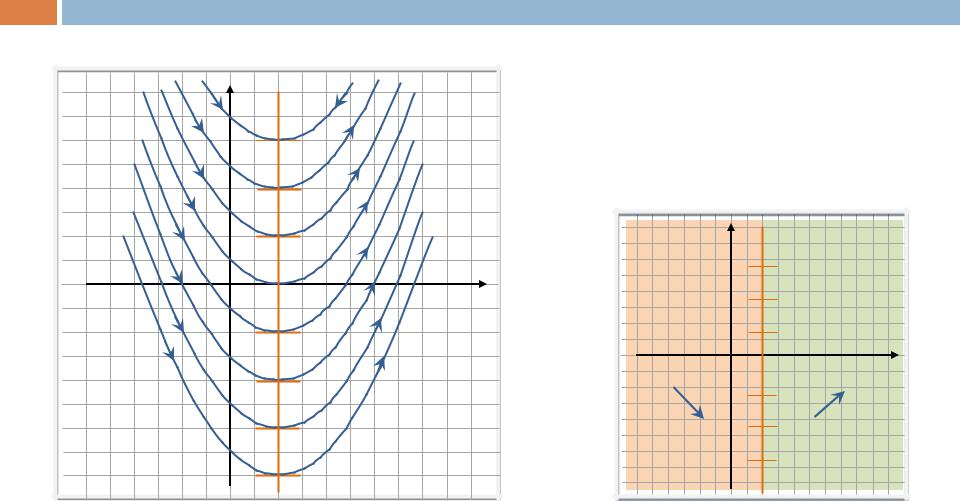
Пример 11.

59

y

x

1

Определить направление движения по фазовым траекториям можно было бы и установив области «знакопостоянства» правых частей системы.

	y
x'(t) > 0,	x'(t) > 0,
y'(t) < 0	y'(t) > 0
	x
	1

Пример 12.

60

dx y,dt

dy y 1.dt

Вертикальная изоклина y = 0; горизонтальная изоклина y 1= 0.

Выясним, существуют ли прямые, которые содержат фазовые траектории. Уравнения таких прямых будем искать в виде y = kx + b. Так как

k

dy

y 1

1

1

1

1

,

dx

y kx b

y

y kx b

y

y kx b

kx b

то последнее выражение не зависит от x, если k = 0. Тогда для нахождения b

получим	0 1	1		b 1.
		b

Таким образом, на прямой y = 1 лежат фазовые траектории. Эта прямая явля-

ется асимптотой на фазовой плоскости.

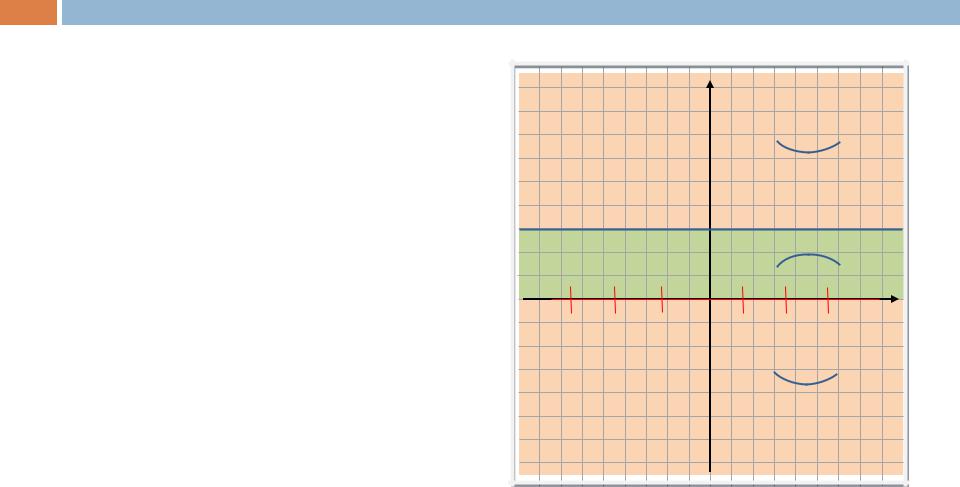
Пример 12.

61

Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории относительно оси x. Для этого найдем производную y”(x):

d 2 y

d

y 1

d

1

y '(x)

y 1

1

,

dx

2

y

y

2

y

3

dx

dx

y

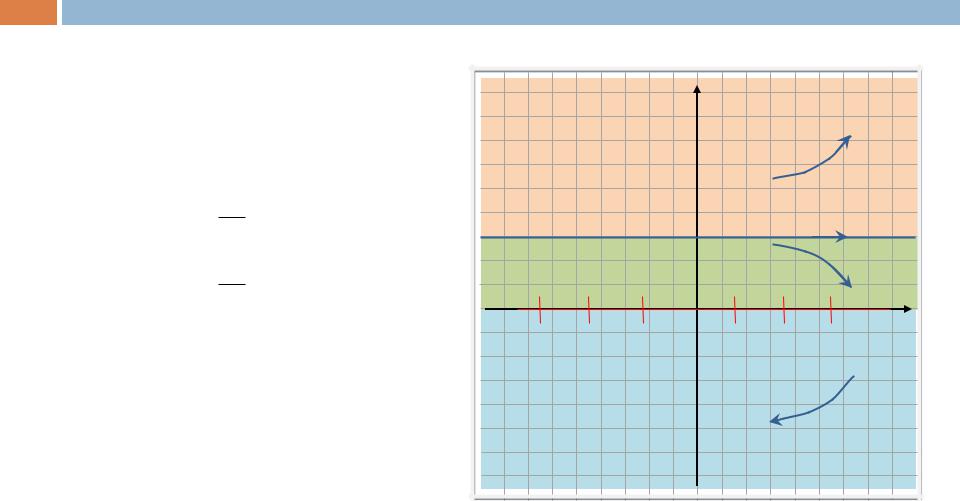
и определим области «знакопостоянства» полученного выражения. В тех областях, где y”(x) > 0, фазовые траектории имеют

выпуклость «вниз», а где y”(x) < 0, –

выпуклость «вверх».

y

y”(x) > 0

y”(x) < 0

x

y”(x) > 0

Пример 12.
62
Выясним направления движения по									y
фазовым		траекториям,			определив
области «знакопостоянства» правых							x’(t) > 0,	y’(t) > 0
частей системы							y”(x) > 0
		dx		y,
		dt
		dy		y 1.			x’(t) > 0,	y’(t) < 0,	y”(x) < 0
									x
		dt
Границами		этих		областей		будут
вертикальная			и	горизонтальная			x’(t) > 0,	y’(t) < 0
изоклины.							y”(x) > 0
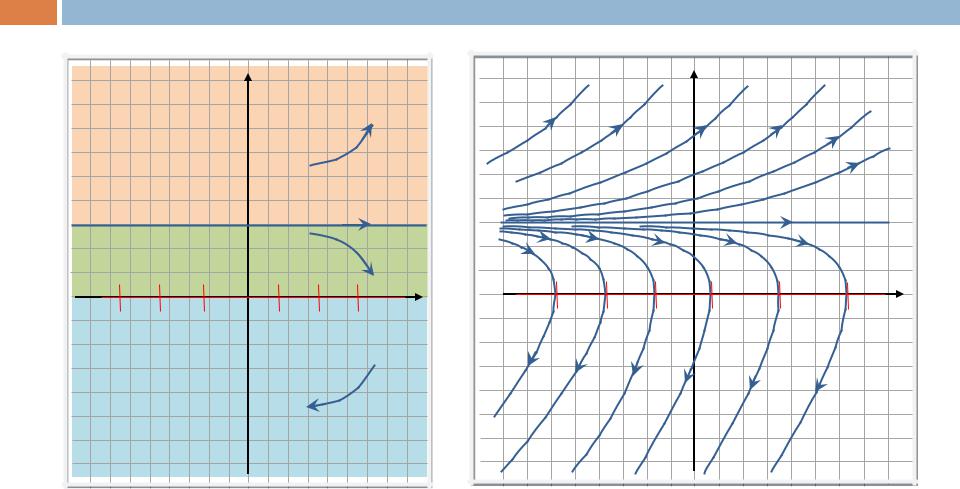
Полученной информации достаточ-
но	для	построения			фазового
портрета.

Пример 12.
63
	y		y
x’(t) > 0,	y’(t) > 0
y”(x) > 0
x’(t) > 0,	y’(t) < 0,
y”(x) < 0		x	x
x’(t) > 0,	y’(t) < 0
y”(x) > 0

Пример 13.

64

dx 2,dt

dy 2x y.dt

Горизонтальная изоклина: 2x y = 0.

Выясним, существуют ли прямые, которые содержат фазовые траектории. Уравнения таких прямых будем искать в виде y = kx + b. Так как

k

dy

2x y

(2 k)x b

,

dx

y kx b

2

y kx b

2

то последнее выражение не зависит от x, если k = 2. Тогда для нахождения b

	получим		b		b 4.
	2
		2

Таким образом, на прямой y = 2x 4 лежат фазовые траектории. Эта прямая является асимптотой на фазовой плоскости.

Пример 13.

65

Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории относительно оси x. Для этого найдем производную y”(x):

d 2 y			d		2x y			2 y '(x)		1		2		2x y			y 2x 4	.
dx	2							2		2							4
			dx		2									2

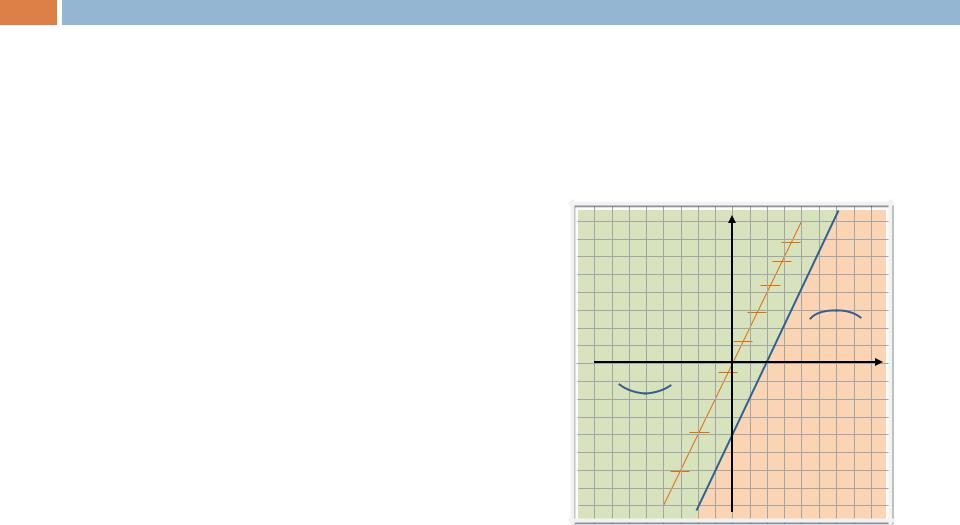
Определим области «знакопостоянства» полученного выражения. В тех областях, где y”(x) > 0, фазовые траектории имеют выпуклость «вниз», а где y”(x) < 0, – выпуклость «вверх».

y

y”(x) > 0

x

y”(x) < 0

Пример 13.

66

Выясним направление движения по фазовым траекториям, определив области «знакопостоянства» правых частей системы:

dx

dt 2,

dy 2x y.

dt

Границей этих областей будет горизонтальная изоклина.

	y
x’(t)>0,	y’(t)<0
		x
	x’(t)>0,	y’(t)>0

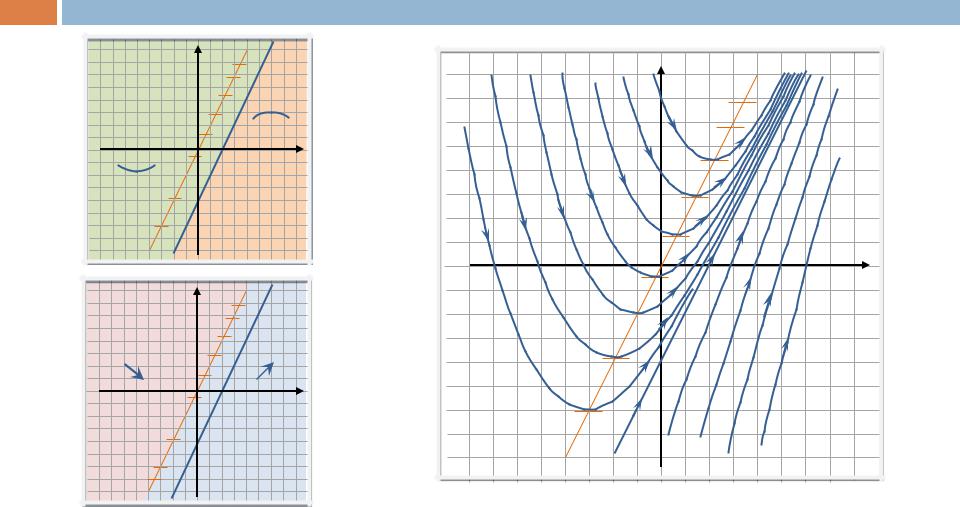
Полученной информации достаточно для построения фазового портрета.

Пример 13.

67

y

y”(x) > 0

x

y”(x) < 0

x’(t)>0,	y
y’(t)<0
	x
	x’(t)>0,
	y’(t)>0

y

x

Пример 14.

68

dx x y,dt

dy 2(x y) 2.dt

Вертикальная изоклина: x y = 0; горизонтальная изоклина: x y + 1= 0.

Выясним, существуют ли прямые, которые содержат фазовые траектории. Уравнения таких прямых будем искать в виде y = kx + b. Так как

	dy			2(x y) 2						2
k								2
	dx		y kx b	x y		y kx b				x y

то последнее выражение не зависит от x, если

получим	1	2		2		b 2.
				b

2	2	,
	(1 k)x b
y kx b

k = 1. Тогда для нахождения b

Таким образом, на прямой y = x +2 лежат фазовые траектории. Эта прямая является асимптотой на фазовой плоскости.

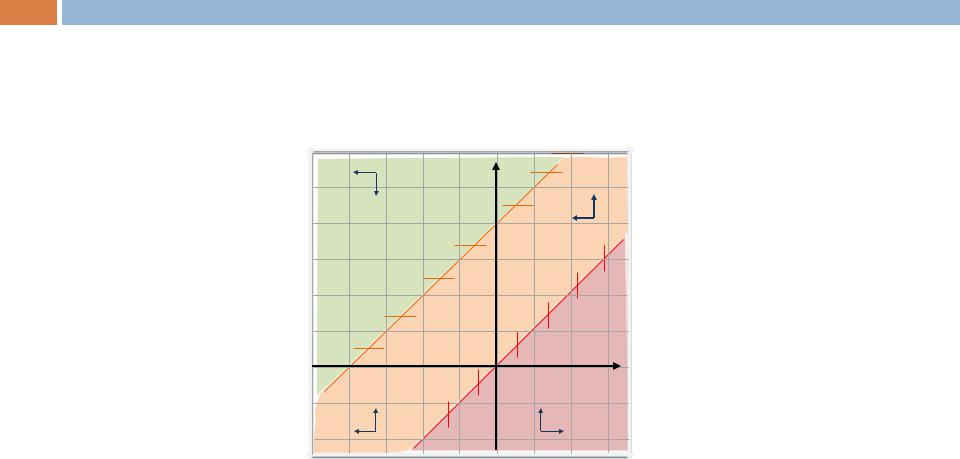
Пример 14.

69

Определим, как изменяются абсцисса и ордината движущейся точки по фазовой траектории. Для этого построим области «знакопостоянства» правых частей системы.

	y
x’(t)<0,	y’(t)<0
	x’(t)<0,	y’(t)>0
			x
		x’(t)>0,	y’(t)>0

Эта информация потребуется для определения направления движения по траекториям.

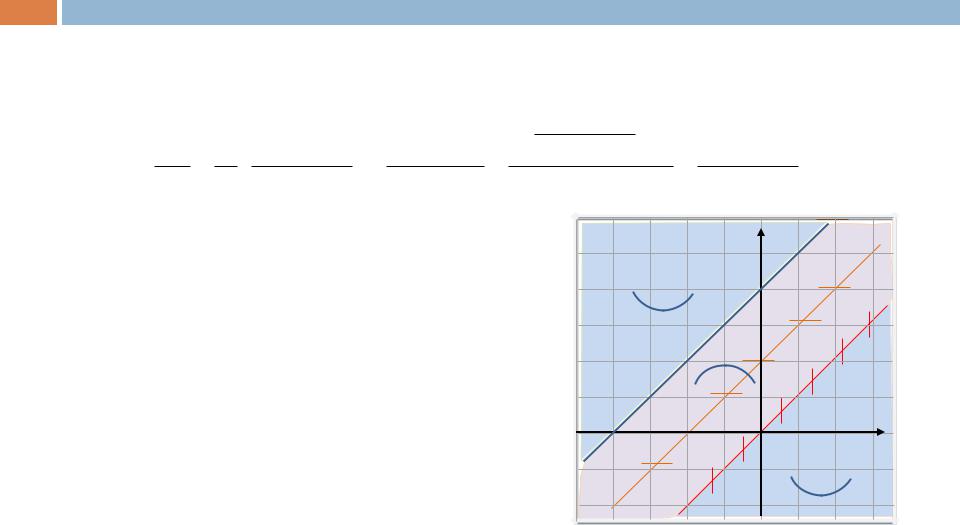
Пример 14.

70

Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории

относительно оси x. Для этого найдем производную y”(x):

2(x y) 2

d 2 y

d

2(x y) 2

2( y '(x) 1)

2

x y

1

2(x y 2)

dx

2

x y

(x

y)

2

(x y)

2

(x y)

3

.

dx

y

Определим

области

«знакопостоянства»

y”(x)> 0

полученного выражения.

В тех областях,

где y”(x) > 0, фазовые траектории имеют

выпуклость

«вниз», а где y”(x) < 0, –

выпуклость «вверх».

y”(x)< 0

x

Полученной

информации

достаточно

для

y”(x)> 0

построения фазового портрета.

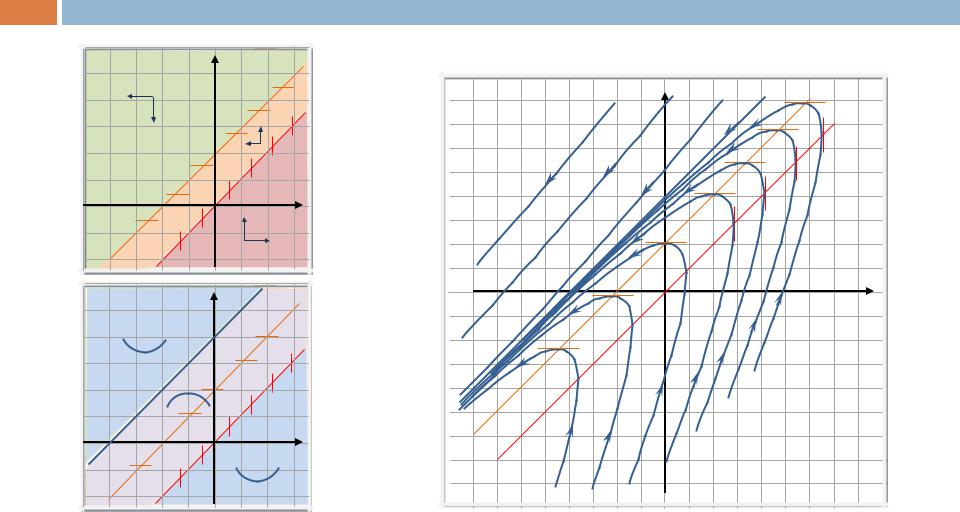
Пример 14 (ФП)

71

y

x

y

x

y

x