posobie_tvp__elektromagnitniie_volnii

→ →	1		E2					j δ
•
Π = z 0				mx			е−2 α zе	2
	2			•
								(4.60)
				Z с

и содержит как действительную, так и мнимую части. Это означает, что имеется как активный, так и реактивный поток мощности. Средняя за период плотность потока мощности экспоненциально убывает вдоль оси z

•

E2

δ

→

→ →

Πср = ReΠ = z

0

mx

е−2αz cos

•

2 .

(4.61)

Zс

Возникновение

плотности

потока

реактивной

энергии

→

•

в среде с

σ ≠ 0

может

быть

объяснено следующим

Im П

образом. При распространении электромагнитной волны в среде

→ →

возникают электрические токи с плотностью J = σE , на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи излучают электромагнитное поле, создают вторичную электромагнитную волну, которая складывается с первичной и происходит непрерывный обмен энергией между волной и средой, что и приводит к возникновению потока реактивной мощности.

Скорость распространения энергии вычисляется по формуле

(3.65)

	→		1
→	Πср	→
V Э =	wср	= z 0 εаµа	1 + tg	2	.	(4.62)
					δ +1
		2

Как видно из (4.62) скорость распространения энергии зависит от частоты. Основное отличие параметров плоской волны, распространяющейся в среде с конечной проводимостью и в среде с σ = 0 состоит в том, что в среде без потерь параметры волны

(Vф, Vэ, Zс и др.) одинаковы при любых частотах, а в среде с

проводимостью они зависят от частоты. Зависимость фазовой скорости волны от частоты называется дисперсией. Следует

81

отметить, что если есть необходимость учесть другие потери, например, магнитные, то следует воспользоваться изложенным способом определения коэффициента фазы, коэффициента затухания и характеристического сопротивления среды и всеми последующими преобразованиями.

Рассмотрим два частных случая реальных сред: диэлектрики с малыми потерями и хорошо проводящие среды (проводники).

4.3.1. Плоские однородные волны в диэлектрических средах с малыми потерями

Диэлектрики с малыми потерями tg δ <<1 широко используются в аппаратуре радиоэлектроники и связи. Обычно это немагнитные диэлектрики с µ = 1. Выведем приближенные формулы для расчета основных параметров плоской электромагнитной волны в таких материалах. Воспользуемся абсолютной комплексной диэлектрической проницаемостью (4.42)

ε•а = εа(1− j tg δ)

и комплексным волновым числом (4.43)

•	= ω µoεа	1 − j tgδ .
k = ω µ0εа(1− j tgδ)			(4.63)
Поскольку tg δ << 1 , то корень	1 − j tg δ	можно разложить в
ряд Тейлора, сохранив два первых члена разложения
1− j tg δ ≈1− j 1 tg δ.			(4.64)
2

Выражение (4.64) подставляем в (4.63) и выделяем реальную и мнимую части комплексного волнового числа

•		− j	1		= ω µ0εа − j	σ	µ	0 = β− jα.	(4.65)
k = ω µ0εа 1			2	tgδ		2
							εа

Получаем приближенные выражения для коэффициента фазы и коэффициента затухания

β = ω µ			ε	а	= ω ε ε µ		= ω ε =		2π ε	,	(4.66)
		0				0 0		C	λ0
α =	σ	µ0			= tgδ	π ε =	1	βtgδ .			(4.67)
	2	εа				λ0	2

Для характеристического сопротивления среды

82

•

µ

0

=

120π

=

120π

1

Z с =

εа(1

ε

1− j tgδ

ε

1 + j

2

tgδ

(4.68).

− j tgδ)

Комплексный

характер

Z с

показывает

на

небольшую

несинфазность

векторов

→

и

→

которой на

практике

можно

E

H ,

пренебречь.

Длина волны вычисляется по обычной формуле

λ =

2π

.

(4.69)

β

Фазовая скорость и скорость распространения энергии

рассчитываются как в среде с σ = 0

Vф =Vэ

=

1

(4.70)

εаµa

Из полученных результатов следует, что параметры волны (β, λ, Vф , Vэ, Zс ), распространяющейся в реальном диэлектрике в

первом приближении совпадают с параметрами волны в среде без потерь. Коэффициент затухания α является малой величиной, не зависит от частоты, дисперсионные свойства проявляются незначительно.

4.3.2.Плоские однородные волны в хорошо проводящих средах

Вхорошо проводящих средах (например, в металлах) tgδ >> 1,

относительная магнитная проницаемость µ = 1	(µа = µ0). При
tgδ >> 1 в общих выражениях коэффициента	фазы (4.46) и

коэффициента затухания (4.47) можно пренебречь единицей по сравнению с tgδ. В результате получаем

β =	ωµ0σ	=	πfµ0σ ,	(4.69)
	2
α =	ωµ0σ	=	πfµ0σ .	(4.70)
	2

Постоянные β и α нелинейно зависят от частоты, следовательно, свойства волны на разных частотах будут существенно различаться. Формулы для фазовой скорости, длины волны и характеристического сопротивления в таких средах принимают вид

83

Vф =Vэ =

2ω

= 2

πf

;

(4.71)

µ0σ

µ0σ

λ = 2π

=

2π

=

2 π

;

(4.72)

β

πfµ0σ

fµ0σ

•

µ

ω

j π

µ

ω

Z с =

0

е 4

= (1 + j)

0

σ

2σ .

(4.73)

Сравним параметры плоских волн, распространяющихся в

вакууме и меди ( σ = 5,65 107 См/м) на частоте 1 МГц:

в вакууме

в металле (медь)

Vф =Vэ = 3 108 м/c

Vф =Vэ = 421м/c

λ0 = 300 м

λ = 4,21 10−4 м

Z0 =120π Ом ≈377 Ом

•

≈ 3,74 10−4 Ом.

Z с

Коэффициент затухания волны, распространяющейся в меди при частоте 1 МГц равен α = 14935 1/м. Глубина проникновения волны в медь на частоте 1 МГц составляет 67 мкм. Приведенные примеры показывают, что электромагнитная волна на частотах радиодиапазона практически не проникает вглубь проводника.

4.4. Поляризация электромагнитных волн

Поляризацией электромагнитной волны называют изменения

→ →

величины и ориентации векторов E и H в фиксированной точке пространства в течение периода колебания волны. Волна, у которой в фиксированной точке пространства в любой момент времени

→ →

величина и ориентация векторов E и H являются детерминированными (точно определенными), называется поляризованной. Поляризация волны ориентационная

→ →

характеристика. В плоской однородной волне векторы E и H взаимосвязаны (4.36), характер их поведения в пространстве одинаков, поэтому ограничиваются рассмотрением одного вектора

84

→	→
E . Плоскость, проходящую через вектор	E и направление

распространения волны, называют плоскостью поляризации. Предположим, что волна создается двумя взаимно

перпендикулярными элементарными электрическими вибраторами с токами I1 и I 2 (рис. 4.7).

Рис. 4.7. К введению понятия поляризации волны

→

Вектор E имеет две составляющие Ех и Еу, которые имеют разные амплитуды и изменяются с некоторым фазовым сдвигом в зависимости от соотношения между амплитудами и фазами токов

→

вибраторов. Вектор H при этом также имеет две составляющие Нх и Ну, связанные с Ех и Еу характеристическим сопротивлением.

→

Таким образом, в общем случае выражение для вектора E плоской волны в среде без потерь записывается в виде

→	→					→	Emy cos(ωt − kz + ϕ2 ).
E	= x0	Emx cos(ωt − kz + ϕ1 )+ y0							(4.74)
	Здесь		ϕ1 и	ϕ	2	– начальные фазы составляющих Е		х	и Е	у	в
точке		z = 0	при	t = 0. Волну			(4.74) можно рассматривать как

суперпозицию(сумму) двух плоских волн одинаковой частоты с

	→	и	→
взаимно перпендикулярной ориентацией векторов E x			E y ,
распространяющихся в одном направлении	(вдоль	оси	z).
→	(4.74)	углом Θ
Определим ориентацию суммарного вектора E

(рис. 4.8).

85

				→
Ex			θ	E

Ey

→

Рис. 4.8. Мгновенное положение вектора E

Угол Θ отсчитывается по часовой стрелке, если смотреть вдоль направления распространения волны и определяется

соотношением

Ey

Emy cos(ωt − kz + ϕ2 )

tg Θ =

=

.

(4.75)

E

x

E

mx

cos(ωt − kz + ϕ )

1

→

Характер изменения вектора E (4.74) с течением времени в

фиксированной

точке

пространства

зависит

от сдвига фаз

∆ϕ = ϕ2 − ϕ1

и от равенства или неравенства амплитуд Emx

и Emy .

В общем

случае

угол

Θ

может изменяться во

времени.

Конец

вектора

→

с

течением

времени

в фиксированной

точке

E

пространства будет описывать линию, называемую годографом. По форме годографа выделяют три вида поляризации.

1. Линейная поляризация. Составляющие Ех и Еу синфазны или противофазны

∆ϕ = ϕ2 −ϕ1 = nπ, где n = 0, ± 1, ± 2,…							(4.76).
Для простоты возьмем n = 0, то есть начальные фазы							ϕ1 и ϕ2
совпадают.	Полагая	в	формуле (4.75) ϕ1 = ϕ2 = ϕ ,				получаем
постоянное значение угла ориентации
tg Θ =	Emy cos(ωt − kz + ϕ)				Emy
				=		= const .	(4.77)
	Emx cos(ωt − kz + ϕ)				Emx
		→
Величина вектора		E	(4.74) меняется во времени
				86

→	= Ex2 + E2y = Emx2 + Emy2 cos(ωt − kz + ϕ).
E		(4.78)

→

В фиксированной точке пространства вектор E , не меняя

→

ориентации ( Θ = const) изменяется по модулю, конец вектора E с течением времени перемещается вдоль отрезка прямой линии, составляющей с осью х угол Θ

Θ = (−1)n arctg	Emy	.	(4.79)
	Emx

При четных значениях числа n (Ех и Еу синфазны) угол Θ величина положительная; при нечетных n (Ех и Еу противофазны)

угол Θ величина отрицательная. Таким образом, волна (4.74) при выполнении условия (4.76) имеет линейную поляризацию.

→

Отметим, что если вектор E плоской волны имеет одну составляющую, волна линейно поляризована.

2. Круговая поляризация. Амплитуды составляющих Ех и Еу равны,

а фазы отличаются на ± π2

Emx = Emy = E0, ∆ϕ = ϕ2 − ϕ1 = ± π2 .

(4.80)

Подставляя эти значения в (4.75), получаем равенство

E

ωt − kz + ϕ ±

π

0

cos

msin(ωt − kz + ϕ )

1

2

tg Θ =

=

1

.

(4.81)

E

0

cos(ωt − kz

+ ϕ )

cos(ωt − kz + ϕ )

Из (4.81) следует, что

1

1

π

Θ = +(ωt −kz +ϕ1), если

ϕ2

= ϕ1

−

,

(4.82)

2

Θ = −(ωt −kz +ϕ1), если

ϕ2

= ϕ1

+

π .

(4.83)

2

Θ в

Равенства (4.82),

(4.83)

означают,

что

угол

фиксированной точке пространства изменяется линейно во времени

→

и происходит периодическое изменение ориентации вектора E .

→

Величина вектора E при этом остается неизменной

87

→	= Ex2 + E2y = E0 .
E

Таким образом, в фиксированной точке пространства вектор

→

E , оставаясь неизменным по величине, вращается с угловой

	→	→
частотой ω	вокруг направления z0	. Число оборотов вектора E за

секунду равно частоте колебаний. В рассматриваемую точку в

→

разные моменты времени приходит вектор E разной ориентации.

→

Конец вектора E при этом описывает окружность (рис. 4.9).

→

Рис. 4.9. Годограф вектора E при круговой поляризации

Волна (4.74) при условии (4.80) имеет круговую поляризацию.

→

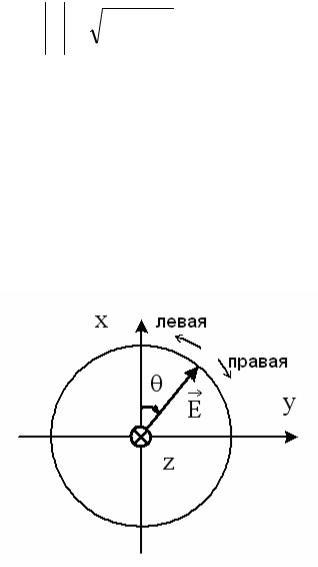
В зависимости от направления вращения вектора E различают волны с правой и левой поляризацией. Волна имеет правую

→

круговую поляризацию, когда вектор E вращается по часовой стрелке, если смотреть вдоль направления распространения волны

( Θ>0). Волна имеет левую круговую поляризацию, когда вектор →

E

вращается против часовой стрелки, если смотреть вдоль

направления распространения волны ( Θ<0). Согласно условиям

→

(4.82), (4.83) вектор E вращается в сторону к отстающей по фазе

→

составляющей. На рис. 4.10 показана ориентация вектора E в

88

пространстве в фиксированный момент времени для плоской волны с круговой поляризацией, распространяющейся вдоль оси z в среде без потерь

λ

t = t0

→

Рис. 4.10. Ориентация вектора E в пространстве при круговой поляризации

Линия, соединяющая концы векторов, представляет собой правовинтовую спираль с шагом, равным длине волны. Ее

проекция	на плоскость XOY		образует	окружность	с вращением
вектора	→	против часовой	стрелки,	глядя вдоль	направления
	E

распространения волны. Отметим, что винтовая линия, соответствующая волне с правой круговой поляризацией, имеет левую намотку, и, наоборот, в случае волны с левой круговой поляризацией винтовая линия имеет правую намотку.

→

Очевидно, такой же анализ для вектора H привел бы к аналогичным результатам. Запишем для примера поле плоской однородной волны левой круговой поляризации, распространяющейся вдоль оси z в среде без потерь. В записи электрического поля используем условие круговой поляризации (4.80), а взаимосвязанное с ним магнитное поле определяем по

→ →

формуле (4.32). Комплексные амплитуды векторов E и H рассматриваемой волны принимают вид

•	→		→
→		E			E e− jkz
E	= x		e− jkz + j y	0		,	(4.84)
	0	0			0

89

		•		E			E
		→	→			→
		H = − j x		0	e− jkz	+ y	0	e− jkz	(4.85)
			0	ZC		0	.
							ZC
	При записи этой волны использовано известное соотношение
± j	π	= ± j . На основании
e	2		последних			выражений (4.84),			(4.85)

находим среднее за период значение плотности потока мощности

→

→

→

•

1

•

*

x0

y0

z0

1

→

E2

E2

→ E2

→

→

→ →

• •

Πср = ReΠ = Re

E, H =

E

x

E

y

0

=

z

0

+

0

= z

0

2

2

0

ZC

0

ZC

.(4.86)

ZC

Hx

H y

0

Среднее значение вектора Пойнтинга волны круговой поляризации равно сумме средних плотностей мощности двух волн с ортогональными линейными поляризациями.

Любая волна круговой поляризации является суперпозицией двух волн с ортогональными линейными поляризациями при условии (4.80). В свою очередь, всякую линейно поляризованную волну можно представить в виде суммы двух волн с правой и левой круговой поляризацией. Вновь воспользуемся комплексным

→

представлением вектора E волны линейной поляризации

•	→
→
E	= x E e− jkz		.	(4.87)
	0	0

Прибавим и вычтем в правой части (4.87) дополнительный вектор и перегруппируем слагаемые

•

→

→

→ →

−jkz

→

−jkz

→

−jkz

→

−jkz

E=x0 E0e

±j y0

0.5E0e

= x0

+j y0

0.5E0e

+ x0

−j y0

0.5E0e .

(4.88)

Первое слагаемое в правой части (4.88) описывает волну с левой круговой поляризацией, а второе слагаемое описывает волну с правой круговой поляризацией с равными амплитудами.

3. Эллиптическая поляризация. Составляющие Eх и Еу (4.74) имеют

→

произвольные соотношения амплитуд и фаз. Суммарный вектор E

90