Минькова. Векторная алгебра и аналитическая геометрия. 2006

Решение.																																(a b ) c					abc
	Воспользуемся формулами (2.17) и (2.25): прс a b																																						.
																																		c				c
Вычислим длину вектора																										и смешанное произведение
																2		( 1)	2	0		2
																								2
										c						1
							2	3		1								9 11						1 11				1 9
			abc				1	9	11							2		1	0		3			1		0	1	1	1		45.
							1	1			0
				45				45
									2
Тогда пр с a b											.
								2
				2
					Примеры для самостоятельного решения
Пример.	Вычислить							объем								треугольной							пирамиды					с	вершинами								A 0, 0,1 ,
B(2, 3, 5),	C(6, 2, 3), D(3, 7, 2). Найти длину высоты, опущенной на грань BCD.

Ответ: V 120 , h 4 17510 .

Пример. Показать, что точки A(5,7, 2), B(3,1, 1), C(9,4, 4), D(1,5,0) лежат в од-

ной плоскости.

3. Аналитическая геометрия

Аналитическая геометрия изучает геометрические объекты (линии, поверхности) алгебраическими (аналитическими) методами. Для этого вводят понятия уравнения линии или поверхности. Уравнением линии или поверхности называют уравнение, которому удовлетворяют координаты всех ее точек и только они.

Мы рассмотрим линиии поверхности, которые имеют уравненияпервой и второй степени.

3.1. Плоскость и ее уравнение

Уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору
Пусть на плоскости задана точка P0 (x0 , y0 , z0 ) и вектор
N {A, B, C}, перпендикулярный плоскости (рис. 32). Вектор						N
N называют нормальным вектором плоскости. Произволь-				P0		P
ная точка P(x, y, z) принадлежит плоскости тогда и только
тогда, когда векторы P0 P и N		ортогональны, а значит, их ска-
						Рис. 32
лярное произведение равно нулю:		P0 P N 0, или в координатной
форме
			.			(3.1)
	A( x x0 ) B( y y0 ) C(z z0 ) 0
	Общее уравнение плоскости

Раскроем скобки в уравнении (3.1): Ax By Cz ( Ax0 By0 Cz0 ) 0. Обозначив выражение в скобках через D , получим общее уравнение плоскости

21

Ax By Cz D 0

.

(3.2)

Отметим, что коэффициенты A, B, C есть координаты нормального вектора плоскости. Уравнение плоскости (3.2) есть уравнение первой степени относительно x , y , z . Справедливо и обратное: всякое уравнение первой степени определяет

плоскость.

Неполные уравнения плоскости

Выделим следующие случаи:

1). Если в уравнении плоскости отсутствует переменная x , то плоскость па-
раллельна оси ox .
2). Если в уравнении плоскости отсутствует переменная y	(или z ), то плос-
кость параллельна оси oy (или oz ).
3). Если в уравнении плоскости отсутствуют две переменные, например,		x и
y , то плоскость параллельна плоскости xoy.
Действительно, если уравнение плоскости имеет вид:	By Cz D 0	(от-
сутствует x ), то нормальный вектор плоскости N {0, B, C}	перпендикулярен

оси ox , а значит, сама плоскость параллельна оси ox . Если в уравнении плоскости отсутствуют x и y , то плоскость параллельна осям ox и oy , а значит, и плоскости xoy .

Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей

Угол между плоскостями w1 и w2 определяется как угол между их нормальными векторами N 1 и N 2 (рис. 33). Поэтому

								w2
cos	N1	N 2						w1
			.	N			2
	N1		N 2		1	N

Плоскости параллельны тогда и только тогда, когда их

нормальные векторы N 1 {A1 , B1 , C1} и				N 2		{A2 , B2 , C2 }					Рис. 33
коллинеарны, т.е.
			A1			B1		C1	.
	N1	|| N2 или
			A2			B2
								C2

Плоскости ортогональны тогда и только тогда, когда их нормальные векторы ортогональны, т.е.

	A1 A2 B1 B2 C1 C2 0.
N1 N2 0 или

Расстояние от точки до плоскости

Рассмотрим плоскость (рис.34) с уравнением Ax By Cz D 0 и точку P1 x1 , y1 , z1 . Опустим из точки P1 на плоскость перпендикуляр P1O и рассмотрим на плоскости точку P2 ( x2 , y2 , z2 ) . Вычислим искомое расстояние

22

											N
										P1
				P P N
				2 1							P2
d P O	пр P P								.
1	N 2 1
					N					0

Запишем это равенство в координатной форме, учитывая, что

P2 P1 {x1 x2 , y1 y2 , z1 z2 },

Рис. 34

N A, B, C :

d

A( x1 x2 ) B( y1 y2 ) C(z1 z2 )

( Ax1 By1

Cz1 ) ( Ax2

By2 Cz2 )

.

A2 B2 C2

A2 B2 C2

Точка P2

лежит на плоскости, поэтому ее координаты удовлетворяют уравне-

нию плоскости, т.е. Ax2 By2 Cz2

D. Учитывая это, получим формулу для

вычисления расстояния от точки P1 (x1 , y1 , z1 ) до плоскости Ax By Cz D 0

d

Ax1 By1 Cz1 D

.

(3.3)

A2 B2 C2

Пример 3.1.

Найти расстояние от точки

P1 ( 1,4,5) до плоскости,

проходящей

через точку P0 (3, 1,0) и перпендикулярной вектору

N {4, 2,1}.

Решение. Запишем уравнение плоскости, проходящей через точку P0 и перпен-

используя формулу (3.1):

дикулярной вектору N ,

4(x 3) 2( y 1) 1(z 0) 0 ,

или 4x 2 y z 14 0 .

Найдем расстояние от точки P1 ( 1,4,5)

до этой плоскости по формуле (3.3)

d

4 ( 1) 2 4 5 14

21

z

21.

3

42 ( 2) 2 12

21

Пример 3.2. Построить плоскости с уравнениями

4

y

2x 3y 4z 12

и 3x 2 y 6.

Найти угол между этими

6

плоскостями.

x

Рис. 35

Решение. Первое уравнение – полное, содержит

x, y, z .

Для построения плоскости удобно найти точки пересечения

z

плоскости с осями координат:

y

если y z 0,

то

x 6 ;

2

3

если

x z 0,

то

y 4 ;

Рис. 36

если

x y 0,

то

z 3.

x

Построим эти три точки M 1 (6,0,0) , M 2 (0, 4, 0),

M 3 (0, 0, 3)

и проведем через них

плоскость (рис. 35).

Во втором уравнении 3x 2 y 6 отсутствует z ,

значит,

это уравнение оп-

ределяет

плоскость, параллельную

оси

oz

и

проходящую

через прямую

3x 2 y 6 , лежащую в плоскости xoy (рис.36).

Для отыскания угла между плоскостями запишем их нормальные векторы

{3,2,0} и найдем угол между этими векторами:

N1 {2,3,4}, N 2

cos	N	N				2 3 3 2 4 0			0.63,	arccos 0.63 51 .
	1		2
	N1		N2			22 32 42		32 22 0

23

x y 1 0.

Пример 3.3. Составить уравнение плоскости, проходящей через три точки:

A(1,2,3), B(0, 2,1), C( 4, 3,2).

Решение. Точка M (x, y, z) принадлежит искомой плоскости (рис. 37) тогда и

только тогда, когда векторы

AM , AB,

AC лежат в одной

плоскости, т.е. компланарны, и, значит, их смешанное про-

B

M

изведение равно нулю :

x 1

y 2

z 3

A

C

AM , AB, AC

0 1

2 2

1 3

0.

Рис. 37

4 1 3 2

2 3

Отсюда (x 1)( 6) ( y 2)( 9) (z 3)( 15)

0 , или 2x 3y 5z 11.

Примеры для самостоятельного решения

Пример. Написать уравнение плоскости, проходящей через точку M 0 (1,1,1) па-

раллельно плоскости

2x y z 1 0.

Вычислить расстояние

между

этими

плоскостями.

1

Ответ: 2x y z 2 0;

d

.

6

Пример. Написать уравнение плоскости, проходящей через заданные точки M1 (1,2,0), M 2 (2,1,1) перпендикулярно плоскости

Указание: использовать компланарность векторов					и нормального
		M1M ,	M1 M 2
вектора N заданной плоскости.
Ответ: x y 3 0.
Пример. Написать уравнение плоскости, проходящей через точку M 0 (0,1,2) па-
раллельно векторам a1 {2,0,1},	a2 {1,10}. Нарисовать эту плоскость.
Указание: использовать компланарность векторов
		M 0 M ,	a1 ,	a2 .

Ответ: x y 2z 5 0.

3.2. Прямая на плоскости и в пространстве

Канонические и параметрические уравнения прямой

Пусть известна точка M 0 (x0 , y0 , z0 ) , лежащая на прямой (рис. 38), и вектор

									направляющим	вектором
l {m, n, p}, параллельный прямой (он называется
прямой). Точка M (x, y, z) принадлежит прямой тогда и только
тогда, когда векторы M 0 M {x x0 , y y0 , z z0 } и										l
									l {m, n, p}	M
коллинеарны, а значит их координаты пропорциональны:
									M 0
		x x0		y y0		z z 0
								.	(3.4)	Рис. 38
		m		n		p

Полученные уравнения называют каноническими уравнениями прямой впространстве. Обозначив коэффициент пропорциональности в соотношении (3.4) через t ,

получим параметрические уравнения прямой в пространстве:

24

x x0 mt,

y y0 nt,

z z0

pt

.

(3.5)

На плоскости xoy уравнения прямой будут иметь вид:

x x0

y y0

или

.

(3.6)

x x0 mt,

y y0

nt

m

n

x 1

y 2

z 3

Пример 3.4. Найти угол между прямой

и прямой

x 3t 4,

2

1

2

y 4t 5,

z 5t 1. Записать уравнение плоскости, проходящей через прямые.

Решение.

Из канонических уравнений первой прямой следует,

что ее направ-

{ 1,2,2} и ее точка M1 (1, 2,3) . Из параметрических уравнений

ляющий вектор l1

второй прямой следует,

что ее направляющий вектор l2 {3,4,5} и ее точка

M 2 ( 4,5, 1) . Угол между прямыми совпадает с углом между их направляю-

щими векторами, поэтому cos вычислим, используя формулы (2.14):

cos

l1 l 2

1 3 2 4 2 5

15

1

;

.

4

l1

l 2

( 1)2 22 22 32 42 52

3 5 2

2

Точка M (x, y, z) принадлежит плоскости, проходящей через

(рис. 39), тогда и только тогда, когда векторы
									M1M ,	l1,	l 2
значит их смешанное произведение равно нулю:
				x 1	y 2	z 3		0 .
(M1M , l1, l 2 )				1	2	2
				3	4	5

Раскрывая определитель, получим уравнение искомой плос-

кости (x 1) 2 ( y 2) ( 11) (z 3) ( 10) 0 , или 2x 11y 10z 50 0 .

заданные прямые − компланарны, а

M	M1	l1
		l2

M 2

Рис. 39

Пример

3.5. Найти точку Q, симметричную точке

P(2, 5,7)

относительно прямой

x 5

y 4

z 6

.

P

3

l

1

2

P0

l

Решение. Проведем через точку P(2, 5,7) плоскость,

Q

перпендикулярную заданной прямой l (рис. 40). На-

правляющий вектор прямой l {1,3,2}

одновременно яв-

Рис. 40

ляется нормальным вектором плоскости, поэтому ее

уравнение (3.1) примет вид: 1 (x 2) 3 ( y 5) 2 (z 7) 0. Уравнение заданной прямой запишем в параметрическом виде:

x t 5, y 3t 4,	z 2 t 6.	(3.7)
Найдем точку пересечения P0 прямой и плоскости, подставив x, y, z		из уравне-
ния прямой (3.7) в уравнение плоскости:	(t 5 2) 3(3t 4 5) 2 (2 t 6 7) 0.

Получим значение параметра t 2, соответствующее точке пересечения P0 прямой и плоскости. Из уравнений прямой (3.7) при t 2 получим координаты ее точки P0 (3, 2,2). Точка P0 является серединой отрезка PQ, поэтому ее координаты равны полусумме соответствующих координат точек P(2, 5,7) и

25

M 0 (x0 , y0 , z0 )

Q( x, y, z) :	3	x 2	,	- 2	y - 5		,	2	z 7	. Следовательно, искомая точка Q
	2					2		2
имеет координаты: x 4,				y 1,		z 3.

Общие уравнения прямой в пространстве

Пусть прямая l является линией пересечения двух непараллельных плоскостей w1 и w2 (рис. 41). Тогда координаты всех точек прямой удовлетворяют уравнениям первой и второй плоскости, т.е. системе уравнений

	A x B y C z D 0,						(3.8)
	1	1	1		1	0.
	A x B y C			2	z D
	2	2			2

N2 N1

w2 l

w1

Рис.41

Система уравнений (3.8) называется общими уравнениями прямой в пространстве.

Пример 3.6. Записать канонические уравнения прямой, заданной общими

3x 2 y 2z 3 0,

уравнениями:

2x 3y z 4 0.

Решение. Найдем точку на прямой. В системе, определяющей прямую, два уравнения и три неизвестных. Поэтому одно неизвестное выберем произвольно, например z 1, подставим в систему и найдем два других неизвестных: x 1, y 1. Таким образом, на прямой найдена точка M 0 (1,1,1). Плоско-

{2,3, 1}. Направ-

сти, задающие прямую, имеют нормальные векторы N1 {3, 2, 2}

и N 2

ляющий вектор прямой l перпендикулярен этим нормальным векторам (рис.41). Поэтому

i

j

k

l N1 N2

3

2

2

4 i 7 j 13 k.

2

3

1

Тогда канонические уравнения (3.4) прямой примут вид:

x 1

y 1

z 1

.

4

Угол между прямой и плоскостью

7

13

Угол между прямой и плоскостью есть угол между пря-

мой и ее проекцией на плоскость (рис. 42). Рассмотрим

N

l

дополнительный угол 2

. Тогда

N l

sin cos cos (N , l )

.

Рис. 42

N

l

Здесь N − нормальный вектор плоскости,

l − направляющий вектор прямой.

Расстояние от точки до прямой в пространстве

Для отыскания расстояния d от точки M1

до прямой l (рис. 43) опустим

перпендикуляр из точки M1

на прямую l . Пусть M0

− известная точка на пря-

мой, l − направляющий вектор прямой. Рассмотрим параллелограмм, построен-

26

ный на векторах

С одной стороны, площадь

M0M1 и

l .

параллелограмма

S d

.

С

другой

стороны,

l

. Поэтому d

и, значит,

S

M0 M1

l

l

M0 M1 l

расстояние d от точки M1

до прямой l , проходящей через

точку M0 , можно вычислить по формуле

d

M

0 M1

l

.

l

M1

d

l l

M0 Рис. 43

(3.9)

Уравнение прямой на плоскости с угловым коэффициентом

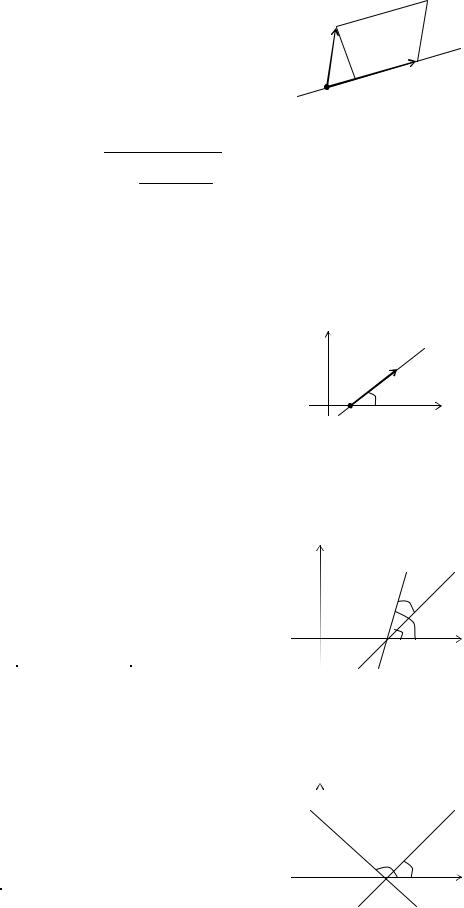
Рассмотрим прямую на плоскости. Пусть − угол наклона прямой к оси

ох (рис. 44). Тогда направляющий вектор

l единичной длины имеет координа-

ты

m cos ,

n cos

sin .

Поэтому

каноническое

y

2

x x0

y y0

уравнение

прямой

(3.6) примет

вид:

, или

l

cos

sin

( y y0 ) tg ( x x0 ) . Число k tg есть угловой коэффициент

x

прямой; уравнение прямой на плоскости с угловым коэффи-

0

циентом имеет вид:

.

(3.10)

Рис. 44

( y y0 ) k(x x0 )

Если на плоскости xoy заданы две прямые с известными угловыми коэффи-

циентами

k1 tg 1 и

k2 tg 2

(рис.45), то можно найти угол между этими

прямыми:

tg 2

tg 1

y

tg tg( 2 1)

или

l

l

2

1

1 tg 1 tg 2

1

2

tg

k

2

k

.

(3.11)

1

0

x

1 k1 k2

Параллельность прямых l

1 ,

l2

равносильна равенству уг-

Рис. 45

лов наклона 1 ,

2

и, следовательно, равенству угловых

коэффициентов k1 и

k2 :

.

(3.12)

l1 || l2 k1

k2

Для перпендикулярных прямых l1

и l2 (рис.46) имеем 2 1

,

y

l

l2

2

1

1

1

k

tg

tg(

) ctg

, т.е.

2

2

2

1

1

2

tg 1

k1

0

1

x

l1 l2

k2

1

.

(3.13)

k

Рис. 46

1

27

Примеры для самостоятельного решения

Пример. Записать уравнение прямой, проходящей через точки M1(0, 2,1),

M 2 (1, 2, 3).							Ответ:				x		y 2		z 1	.
										1
												4		2
Пример. Убедиться, что прямые l :	x 1		y			z 2	и l		:	2x 2 y z 10 0
								2
1	3		1		4							x y z 11 0

параллельны. Написать уравнение плоскости, проходящей через эти прямые.

Указание:	найти направляющий вектор прямой l1 , точку M 2 на прямой l2 и
использовать компланарность векторов M1 M , M1M 2 и l1.
Пример.	Ответ: 5x 11y z 7 0.
	Найти проекцию точки P(1,0, 2) на плоскость 6x 5 y 7z 90 0.
Указание:	написать уравнение прямой, проходящей через точку Р перпендику-

лярно заданной плоскости, и найти точку пересечения этой прямой и плоско-

сти.								Ответ: ( 5, 5,5).
Пример. Убедиться, что прямая	x 1			y 2		z 1		параллельна плоскости
	3			1		8

2x 2 y z 7 0. Найти расстояние между прямой и плоскостью.

Указание: проверить ортогональность направляющего вектора прямой и нормального вектора плоскости. Найти точку на прямой и расстояние от этой точки до плоскости. Ответ: d 4 / 3.

3.3. Кривые второго порядка

Кривые второго порядка – это линии на плоскости, которые описываются уравнениями второго порядка. Установлено, что к кривым второго порядка относятся окружность, эллипс, гипербола, парабола. Других кривых второго порядка нет, если не учитывать случаи вырождения кривой в точку или прямые.

Кривые второго порядка играют важную роль в естествознании. Например, траектории движения планет есть эллипсы. В физике широко используются оптические свойства кривых второго порядка, например, на них основано устройство прожектора.

Эллипс и его уравнение

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, постоянна и больше расстояния между фокусами.

Выведем уравнение эллипса. Пусть F1 и F2 − фокусы эллипса. Расстояние между ними обозначим через 2c , а постоянную сумму расстояний от любой точки М эллипса до фокусов обозначим через 2a . По определению эллипса,

MF1 MF2 2a и 2a 2c, т.е. a c.

Выберем систему координат так, чтобы ось ox проходила через фокусы, а ось oy – посередине между ними (рис. 47). Тогда координаты фокусов

28

F1 c, 0 , F2 ( c, 0). Если M (x, y) − произвольная точка эллипса,

то

x c 2 y2 ,

MF1

MF2

(x c)2 y2

y

и сумма этих расстояний постоянна и равна 2a , т.е.

M

(x c)2 y2 (x c)2 y2 2a.

x

Преобразуем это уравнение к более удобному виду. Перене-

F1

F2

сем один из радикалов в правую часть и возведем обе части

уравнения в квадрат:

Рис. 47

2

2a

2 ,

( x c)2 y2

( x c)2 y2

x2 2xc c2 y2 4a2 4a

x2 2xc c2 y2 .

( x c)2 y2

После упрощения получим

a (x c)2 y 2 a 2 cx.

Еще раз возведем в квадрат обе части уравнения и сгруппируем подобные чле-

ны: (a 2 c 2 )x 2 a 2 y 2 a 2 (a 2 c 2 ).

Так как a c , то разность a 2 c 2 положительна; обозначим ее b2 и разделим обе части полученного равенства на a 2 b2 . В результате получим

		x2		y2	1	.	(3.14)
		a2		b2
Это уравнение называется каноническим уравнением							эллипса. Здесь

b 2 a 2 c 2 . В частном случае при b a уравнение (3.14) примет вид: x 2 y 2 a 2 , т.е. определяет окружность радиуса a с центром в начале координат. Таким образом, окружность есть частный случай эллипса.

Используя уравнение эллипса, установим ряд его свойств.

1). Эллипс симметричен относительно осей и начала координат. Действитель-

но, его уравнение содержит x и y только во второй степени. Поэтому, если пара чисел ( x, y) удовлетворяет уравнению (3.14), то пары ( x, y) , ( x, y) , ( x, y) также удовлетворяют этому уравнению. Другими словами, если точка M (x, y) лежит на эллипсе, то точки M1 (x, y), M 2 ( x, y), M 3 ( x, y) , симметричные точке M соответственноотносительно оси ox , оси oy и начала координат, также лежат на эллипсе.

2). Ввиду симметрии эллипса достаточно исследовать его уравнение в 1−й чет-

верти, где x 0, y 0. Из уравнения (3.14) получим y ba a 2 x 2 . Эта функция

определена при x a, равна нулю при x a, равна b при x 0 и убывает с ростом x . Учитывая это, построим эллипс в 1−й четверти (рис. 48). Используя симметрию эллипса, построим его в остальных четвертях (рис. 49).

	y			y	B1 (0, b)		y	B1
	b			F2	F1	x		M 0
	F1	x
			A2	( a,0)	0	A1 (a,0)	A2	A1
		a
	0 c				B2 (0, b)			B2
							0	x
	Рис.48			Рис. 49
								Рис. 50

29

Точка O называется центром эллипса, отрезки A1 A2 и B1 B2 − осями эллипса.

Точки пересечения эллипса с его осями A1 , A2 , B1 , B2

называются вершинами эллипса.

Если центр эллипса смещен в точку M 0 (x0 , y0 ) , а оси эллипса параллельны

осям координат (рис. 50), то уравнение эллипса примет вид:

( x x )2

( y y

)2

1

.

(3.15)

0

0

a2

b2

Пример

3.7.

Установить,

какая

линия

определяется

уравнением

2x 2

3y 2

4x 18 y 17 0 , и изобразить ее на чертеже.

Решение. Объединим слагаемые с x

в одну скобку, слагаемые с

у – в другую

скобку и вынесем за скобки коэффициенты при x 2

и при y 2 :

2(x2 2x) 3( y2 6 y) 17 0.

y

1

Выражение в скобках дополним до полного квадрата:

0

x

2

2

17 0.

2 x

2x 1 1

3 y

6 y 9 9

F2

3 M 0

F

Тогда 2(x 1)2 2 3( y 3) 2

27 17 0 или

2(x 1)2

3( y 3) 2 12.

1

Разделим уравнение на 12 :

Рис. 51

(x 1) 2

( y 3) 2

1.

6

4

Получили уравнение вида (3.15), причем x

1,

y

0

3, a2 6,

b2

4. Это урав-

0

нение определяет эллипс с центром M 0 (1, 3),

осями симметрии, параллельными

осям координат,

полуосями

a

, b 2

(рис.

51). Найдем еще межфокусное

6

расстояние F1 F2 . Так как

a 2

c 2

b 2 ,

то

c 2

a 2 b 2 6 4 2.

Таким образом,

c

, межфокусное расстояние

F1 F2

2c 2

2

2.

Гипербола и ее уравнение

Гиперболой называют множество точек плоскости, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Пусть F1 и F2 − фокусы гиперболы и межфокусное расстояние F1 F2 2c. Обозначим постоянную разность расстояний от любой точки M (x, y) гиперболы

до фокусов через 2a . По определению гиперболы,

MF1

MF2

2a и

2a 2c. В

правой части равенства выберем знак "+", если

MF1

MF2

, и знак

"–", если

MF1

MF2

(рис. 52).

Выберем прямоугольную систему координат так же, как

и в случае эллипса. Тогда

M

M

MF

( x c) 2 y 2

,

MF

( x c) 2

y 2 .

1

2

Разность этих расстояний равна 2a , т.е.

F2

0

F1

Рис. 52

(x c)2 y 2

(x c)2 y 2 2a.

30