Минькова. Векторная алгебра и аналитическая геометрия. 2006

Проводя вычисления, такие же как в случае с эллипсом, получим

(c 2 a 2 )x 2 a 2 y 2 a 2 (c 2 a 2 ).

Так как c a,	то разность c 2 a 2 − положительна; обозначим ее b2							и разделим
полученное уравнение на a 2 b2 . Тогда уравнение примет вид
			x2		y2	1	,	(3.16)
			a2
					b2

которое называют каноническим уравнением гиперболы. Здесь b2 c2 a2.

Исследуем уравнение гиперболы.

1). Гипербола симметрична относительно осей координат и начала координат, так как уравнение гиперболы содержит x и y только во второй степени. Оси координат есть оси симметрии гиперболы, а их пересечение – ее центр.

2). Ввиду симметрии гиперболы достаточно исследовать уравнение гипербо-

лы в

первой

четверти, где

x 0, y 0.

Из

уравнения

(3.16)

получим

b

. Эта функция определена при

равна нулю при x a и воз-

y

x 2 a 2

x a,

a

растает с ростом x. При неограниченном возрастании x число a 2

мало по

сравнению с

x 2 и функция

b

будет близка к

функции

y

x 2

a 2

a

b

b

b

x,

т.е. гипербола будет приближаться к прямой

y

x.

Учитывая

y

x 2

a

a

a

это исследование, построим гиперболу в первой четверти (рис. 53). Используя симметрию гиперболы, построим ее в остальных четвертях (рис. 54).

Прямые y b x и

y b x , к которым приближается гипербола с ростом х,

a

a

A1 a,0 ,

называются асимптотами гиперболы.

Точки

A2 ( a, 0) называются вер-

шинами гиперболы.

y

F1

y

y

B1

F

A

A

F

b

b a

b

2

2

0 a

1

1 x

0

x

0

a

x

B2

F2

Рис. 53

Рис.54

Рис.55

Для построения гиперболы удобно сначала построить прямоугольник с центром в начале координат и сторонами длиной 2a и 2b, параллельными осям координат (рис. 54); затем построить асимптоты, продолжив диагонали прямоугольника, и через вершины гиперболы провести две ее ветви, приближающиеся к асимптотам.

	Уравнение	y2		x2	1 также определяет гиперболу. Она называется со-
		b2		a2
	пряженной гиперболой.				При x 0 получаем	y b , т.е. эта гипербола имеет
	вершины B1(0,b) и B2(0, b) (рис. 55).

31

Если центр гиперболы находится в точке M 0(x0, y0) , а оси симметрии параллельны осям координат, то уравнение гиперболы имеет вид:

							( x x )2				( y y				)2	1			,	(3.17)
									0					0
								a	2				b	2
	а уравнение ее асимптот						( y y0 )					b	(x x0 )				.
												a
	Пример 3.8. Установить, какая линия определяется уравнением
		1						, и изобразить ее на чертеже.
	x 2			y 2	2 y 5
	2																	1
	Решение. Запишем уравнение линии в виде
													x 2							y 2 2 y 5.
																		2

Отсюда видно, что x 2 0 или x 2. Возведем обе части равенства в квадрат:x 2 2 14 y2 2y 1 4 , или 4 x 2 2 (y 1)2 4 , или y

x 2 2	(y 1)2	1.
1	4
Получили уравнение вида (3.17), где x0			2,	y0 1,	a 1, b 2 .
Это уравнение определяет	гиперболу		с центром M 0 ( 2, 1),

осями симметрии, параллельными осям координат. Первоначальному уравнению соответствует только часть гиперболы, а именно – те ее точки, для которых x 2 (рис. 56).

M 0 1

0 x

Рис. 56

Парабола и ее уравнение

Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.

Пусть F − фокус, прямая CB – директриса (рис. 57).

y

M ( x, y)

Выберем систему координат следующим образом: ось oy

про-

F

ведем через фокус F перпендикулярно директрисе CB ,

а ось

x

ox – посередине между фокусом и директрисой. Обозначив

0

расстояние от фокуса до директрисы через p , получим коор-

C

B

p

динаты фокуса F 0,

. Пусть M (x, y)

− произвольная точка

Рис. 57

2

параболы. По определению параболы,

MF MB , т.е.

2

p 2

p

x

y

y

.

2

2

Возведя в квадрат обе части равенства и упростив, получим

.

(3.18)

x2 2 py

Полученное уравнение называют каноническим уравнением параболы.

32

	Перепишем		это		уравнение в виде y	1	x 2	или
						2 p
	y kx 2 , где k	1		0.	График этой функции хорошо из-
		2 p

вестен (рис. 58). Ось oy		является осью симметрии парабо-
лы	x 2 2 py, а точка	(0,0)	− ее вершиной. Уравнение
x 2	2 py также определяет		параболу (рис. 58) с осью

симметрии oy и вершиной (0, 0) .

Поменяв x и y ролями, получим уравнения парабол:

y

x 2 2 py

x

0

x 2 2 py

Рис. 58

y

y2 2 px ; y2 2 px

.

(3.19)

0

x

y 2 2 px

y 2 2 px

Ось симметрии этих парабол – ось ox (рис. 59), вершина

парабол в точке (0, 0) .

Рис. 59

Уравнение параболы с вершиной, смещенной в

точку M 0 (x0 , y0 ) ,

и осью симметрии,

параллельной оси oy , или параллельной

оси ox , примет соответственно вид:

или

.

(3.20)

(x x0)2 2p(y y0)

(y y0)2

2p(x x0)

Пример 3.9. Построить линию с уравнением y 3 2

. Найти ее фокус.

2 x

Решение. Запишем уравнение в виде y 3 2

и заметим,

что y 3 0 , или

2 x

y 3 . Возведем обе части равенства в квадрат:

y

( y 3)2 4(2 x) , или

( y 3)2

4(x 2) .

Получили уравнение вида ( y y )2 2 p( x x ),

где x 2,

F

M 0

0

0

0

y0 3, 2 p 4, p 2. Это уравнение определяет параболу с

3

вершиной M 0 (2,3)

и осью симметрии, параллельной оси ox .

0 2

x

Первоначальному уравнению соответствует часть парабо-

лы, а именно – те ее точки, для которых y 3 (рис. 60).

Рис. 60

Для отыскания фокуса вспомним, что расстояние от фокуса до директрисы

p 2, а от фокуса до вершины

p

1. Так как вершина M 0 (2,3) , то фокус F (1,3).

2

Пример 3.10. Записать уравнение параболы,

если ее фокус F ( 2,3),

а уравнение

директрисы y 1.

y

Решение. Построим фокус и директрису параболы. Ось

F

3

симметрии параболы проходит через фокус F перпенди-

кулярно директрисе BC (рис.61), а вершина A лежит на

A

x

оси симметрии посередине между фокусом и директрисой.

2

0

yF yB

3 1

Следовательно,

xA xF 2,

yA

1.

B

1 C

2

2

Рис. 61

Так как ось симметрии параболы параллельна оси oy , то

уравнение параболы имеет вид:

(x x A )2

2 p( y y A ). Ветви параболы направ-

33

лены в положительную сторону оси oy , поэтому выбираем в ее уравнении знак «+». Параметр p равен расстоянию между фокусом и директрисой, т.е.

p 3 ( 1) 4. Окончательно уравнение параболы примет вид:	(x 2) 2 8( y 1).
Примеры для самостоятельного решения
Пример. Привести уравнение линии 9x 2 4 y 2 36x 24 y 36	к каноническому

виду и построить линию. Найти межфокусное расстояние. Записать уравнение асимптот.

	Ответ:	(x 2) 2		( y 3)2	1;	2c 2		y 3	3	(x 2).
							13;
		4		9					2

Пример. Установить, часть какой линии задает уравнение:

а) y 1	4				б) x 2		.
			6x x 2 ;
						6 2 y
3
Ответ: а) нижняя часть эллипса, б) правая часть параболы.
Пример. Записать уравнение параболы, если ее фокус F ( 2,3), а уравнение ди-
ректрисы x 4.							Ответ: ( y 3)2	12(x 1).

3.4. Поверхности второго порядка

Поверхности второго порядка описываются уравнениями второго порядка относительно переменных x, y, z. К поверхностям обращаются при изучении

физики, механики, деталей машин, в системах автомати-			z
зированного проектирования.
Среди поверхностей второго порядка выделим					P(		x, y, z)
цилиндрические поверхности. Цилиндрической по-		0
								y
верхностью называется поверхность, состоящая из па-
	x
раллельных прямых (образующих), пересекающих неко-		l
					P0	( x, y,0)
торую линию (направляющую).
Рассмотрим цилиндрическую поверхность, у ко-			Рис. 62
торой образующие параллельны оси оz, а направляющая
l лежит в плоскости xoy и имеет уравнение F (x, y) 0	(рис. 62). Рассмотрим

произвольную точку P(x, y, z) на поверхности. Ее проекция P0 (x, y,0) на плоскость xoy лежит на кривой l . Поэтому координаты точки P0 удовлетворяют уравнению кривой F (x, y) 0 . Этому же уравнению удовлетворяют и координаты точки Р, так как в уравнении не содержится z .

Справедливо и обратное: уравнение F (x, y) 0 определяет цилиндрическую поверхность с образующими, параллельными оси oz , и направляющей,

которая в плоскости xoy имеет уравнение F (x, y) 0 .			z
Аналогично, если в уравнении отсутствует y	(или x ),
то оно определяет цилиндрическую поверхность с обра-				y
зующими, параллельными оси oy (или ox ).		0
		x
Пример 3.11. Построить поверхность с уравнением	z y 2 .
			Рис. 63

34

Решение. В уравнении отсутствует x , значит, уравнение определяет цилиндрическую поверхность, с образующими параллельными оси ох. Направляющая в плоскости yoz имеет уравнение z y 2 , т.е. является параболой с вершиной в начале координат и осью симметрии oz (рис. 63).

Пример 3.12. Построить поверхность

x

2

z

2

1.

z

a 2

b 2

b

Решение. В уравнении отсутствует y , значит, уравнение оп-

ределяет цилиндрическую поверхность с образующими, па-

a

y

раллельными оси oy .

Направляющая в плоскости xoz имеет

x

уравнение

x 2

z 2

1, то есть является эллипсом (рис. 64).

Рис. 64

a 2

b 2

Следующие поверхности также являются цилиндрическими: а)

z 2 y 2

4 ;

б) y x 2 ; в)

z 2 x 2 1. Их построение разберите самостоятельно (рис.65):

a)

z

б)

z

в)

z

2

y

2

1

y

y

1

x

x

x

Рис.65

Кроме цилиндрических поверхностей есть и другие поверхности второго

порядка. Их уравнения содержат все три переменные x, y, z.

Наиболее важные из них:

1)

эллипсоид

x 2

y 2

z 2

1;

c 2

a 2

b 2

2)

коническая поверхность

x 2

y 2

z 2

;

a 2

b2

c 2

3)

параболоид

z

x 2

y 2

;

a 2

b 2

4)

однополостный гиперболоид

x 2

y 2

z 2

1;

a 2

c 2

b 2

5)

двуполостный гиперболоид

x 2

y 2

z 2

1.

a 2

b2

c 2

Построение этих поверхностей по их уравнениям основано на методе сечений, т.е. на построении сечений данной поверхности координатными плоскостями или параллельными им плоскостями. Поясним метод сечений напримерах.

Пример 3.13. Построить поверхность с уравнением z 2 x 2 y 2 .

35

Решение. Так как уравнение поверхности содержит все три переменные, то

	построим поверхность методом сечений. При x 0 (сечение	z
	плоскостью yoz ) исходное уравнение примет вид: z 2 y 2 ,
		h
	или z y . Эти уравнения определяют пару прямых в плос-
	кости yoz (рис. 66). При z 0 (сечение плоскостью xoy ) ис-
	ходное уравнение примет вид: x 2 y 2 0. Оно определяет
	единственную точку O(0,0) . Поэтому рассмотрим дополни-	x
	тельные сечения плоскостями z h. Эти сечения имеют	h
	уравнения x 2 y 2 h2 , т.е. являются окружностями в плос-
		Рис. 66
	костях z h и z h. В итоге получили конус.
	Пример 3.14. Построить поверхность с уравнением x 2 y 2 z 2	1.

Решение. Уравнение поверхности содержит все три переменные, поэтому применим метод сечений. Сечение поверхности плоскостью x 0 (плоскостью yoz ) имеет уравнение y 2 z 2 1. Это уравнение определяет гиперболу в плоскости

yoz . Для определения вершин гиперболы положим y 0				z
и получим z		1 (рис. 67). Сечение поверхности плоско-		2
стью	z 0	имеет уравнение	x 2 y 2 1, которому не
удовлетворяет ни одна пара чисел (x, y), так как всегда				1
x 2 y 2	0 .	Поэтому берем	дополнительные сечения	1
z 2	и получаем уравнение		x 2 y 2 3, которое опреде-

ляет окружности в плоскостях z 2 и z 2 . Полученная	x	2
поверхность называется двуполостным гиперболоидом.		Рис. 67
Построение методом сечений следующих поверх-
ностей разберите самостоятельно (рис.68):

y

y

а)

x 2

y 2

z 2

1;

б) z x 2 y 2 ;

в ) x 2 y 2 z 2 1.

a 2

b 2

c 2

z

z

в)

a)

z

b)

c

b

y

y

y

a

x

x

x

Рис.68

4.Комплексные числа

4.1.Определение, изображение, формы записи

Кпонятию комплексного числа привело стремление решить уравнение

x2 1 0 и извлечь корень из отрицательного числа.

Комплексным числом z называется выражение вида z x iy , где x, y – действительные числа, i − так называемая мнимая единица, i 2 1.

36

Рис. 69

Числа x, y называются соответственно действительной и мнимой частью

комплексного числа z и обозначаются			x Re z,	y Im z.
Если	x 0 , то число 0 iy iy называется			чисто мнимым, если y 0 , то
x i0 x	есть действительное число.
Два комплексных числа считаются равными,				если равны их действительные
части и равны их мнимые части, т.е.
		x1 iy1 x2 iy2	x1 x2 , y1 y2 .

Комплексные числа z x iy и z x iy , отличающиеся знаком мнимой час-

ти, называются комплексно-сопряженными.

Комплексное число z x iy изображается точкой М плоскости

с координа-

тами x, y или ее радиус-вектором OM (рис. 69). Длина век-

y

M ( x, y)

тора OM называется модулем комплексного числа z и обо-

y

значается

z

или r :

x2 y2 .

x

x

z

r

OM

0

Угол между радиус-вектором OM и положительным на-

правлением оси ох называют аргументом комплексного числа z . Угол определяется неоднозначно, с точностью до слагаемого 2 k ; договоримся брать то значение , которое заключено между и и обозначать его arg z.

Наряду с алгебраической формой z x iy комплексного числа рассмотрим еще две формы записи.

Так как x r cos , y r sin (рис.69), то комплексное число z x iy можно записать в тригонометрической форме: z r cos i sin . Введя функцию

ei cos i sin , комплексное число можно записать в показательнойформе: z r ei . Итак, имеем три формы записи комплексного числа:

z x iy ;

z r cos i sin ,

z r e i .

Пример 4.1. Записать комплексное число

z 1 i

в тригонометрической и

3

показательной формах.

Решение. Чтобы записать z в тригонометрической форме, найдем

y

его модуль и аргумент:

1

x

1

z

( 1)2 (

3)2 2 ;

z

для правильного отыскания аргумента рекомендуем изобразить

3

Рис. 70

число z на плоскости (рис.

70). Найдем сначала острый угол 1 ,

,

. Тогда

2

дополнительный к углу :

tg

3

и триго-

1

1

1

3

1

3

нометрическая и показательная формы записи числа z 1 i3 будут следующие:

					2				2				2	i
	z 2	cos					i sin				2 e	3 .
					3				3

37

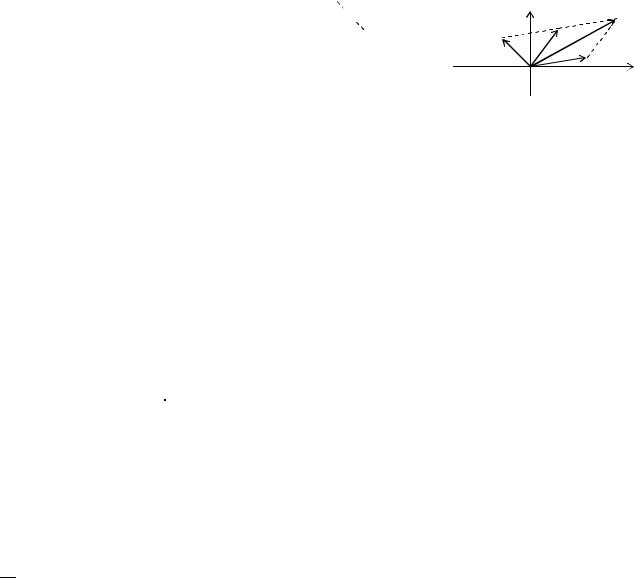
4.2. Действия над комплексными числами

Операции сложения, вычитания, умножения комплексных чисел определяются следующим естественным образом.

1). При сложении (вычитании) двух комплексных чисел складываются (соответственно вычитаются) их действительные и мнимые части, т.е.

z1 z2

(x1 iy1 ) (x2 iy2 ) (x1 x2 ) i( y1 y2 )

.

(4.1)

С геометрической точки зрения сложение (вычитание) комплексных чисел рав-

носильно сложению (вычитанию) изображающих их

y

векторов (рис.71). Отметим, что расстояние между

z1 z2

z1

z1 z2

комплексными точками z1 и z2 равно

z1 z2

. Поэтому

z2

окружность с центром в точке z0 радиуса R имеет урав-

x

нение

z z0

R. .

Рис. 71

2). Умножение двух комплексных чисел в алгебраи-

ческой форме определяется по правилам умножения двучленов с учетом ра-

венства i2 1 :

.

(4.2)

z1 z2 (x1 iy1 ) (x2 iy2 ) (x1 x2 y1 y2 ) i(x1 y2 x2 y1 )

Например,

2 i 3 4 i 6 3i 8 i 4 i2

10 5i .

При умножении двух комплексных чисел в тригонометрической форме

получим:

z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 )

r1 r2 (cos 1 cos 2 sin 1 sin 2 ) i (sin 1 cos 2 cos 1 sin 2 )

r1 r2 cos( 1 2 ) i sin( 1 2 ) .

Следовательно,

z1 z2

z1

z2

,

arg (z1 z2 ) arg z1 arg z2

.

(4.3)

Таким образом, при умножении комплексных чисел их модули умножаются, а аргументы складываются.

3). Деление комплексных чисел определяется как действие, обратное умно-

	жению, т.е. z	z1	, если	z z2	z1 . Практически, при делении двух комплекс-
		z2

ных чисел в алгебраической форме нужно числитель и знаменатель дроби

z1 (z2 0) умножить на число, сопряженное знаменателю; тогда делителем бу-

z2

дет действительное число:

		z a ib						(a ib ) (a ib )						(a a bb ) i (ba a b )
		1	1			1		1	1	2	2			1	2	1 2		1	2	1 2
																						.	(4.4)
		z			a	ib		(a ib ) (a			ib )					a2	b2
Например,		2	2			2		2	2	2	2					2	2
									14 15i2 35i 6 i
2 5i				(2 5i) (7 3i)												29 29 i		1		1 i .
				(7 3i) (7 3i)
7 3i										49 9 i2						49 9			2	2

38

При делении двух комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются, т.е.

	z1			r 1 (cos 1				i sin 1 )				r 1	cos ( 1 2 ) i sin ( 1 2 )	.	(4.5)
												r
	z	2		r	2	(cos	2	i sin	2	)
											2

4). Возведение в степень комплексного числа в алгебраической форме осуществляется по правилам возведения в степень двучлена с учетом того, что

i 2 1, i3 i 2 i i,	i 4 i 2 i 2 1 и т.д. Например,	используя формулу для куба
разности, получим:	(2 i)3 23 3 22 i 3 2 i 2 i3	8 12i 6 i 2 11i.

При возведении комплексного числа z в большую степень удобно использовать его тригонометрическую форму z r cos i sin . Учитывая, что при

умножении модули умножаются, а аргументы складываются, получим формулу Муавра:

zn rn (cos n i sin n ) rnein

.

(4.6)

Пример 4.2. Вычислить z 6 , если z

i.

3

Решение. Изобразим комплексное число z на плоскости (рис. 72),

y

найдем его модуль и аргумент:

1

z

1

x

z

r

3 2 12 2,

tg

,

.

0

3

Тогда

3

6

Рис. 72

z6 r6(cos 6 i sin 6 ) 26(cos i sin ) 64.

5).

Извлечение корня n-ой степени из комплексного числа является дейст-

вием, обратным возведению в степень, т.е.

n

w, если wn z .

z

При извлечении корня из комплексного числа z удобно использовать

тригонометрическую

форму

записи

комплексного

числа.

Пусть

z r(cos i sin ) , w (cos i sin ) . Так как

w n z, то

n(cos n i sin n ) r(cos i sin ).

Уравных комплексных чисел модули должны быть равны, а аргументы могут отличаться на число, кратное 2 , то есть

n r,

n 2 k

или

n

,

2 k

.

r

Подставляя эти значения в выражение n

n

получим:

z

w (cos i sin ),

n

n

2 k

2 k

z

r

i sin

cos

.

(4.7)

n

n

k 0,1, 2, ..., n 1.

Придавая k значения 0, 1, 2, ... , n 1 , получим n различных значений корня n −й степени из комплексного числа. При других значениях k получим значения корня, совпадающие с уже найденными. Например, при k n и при k 0 значения корней совпадают:

39

w n

cos

2 n

i sin

2 n

n

cos

2

i sin

2

n

cos

i sin

w .

r

r

r

n

n

n

n

0

n

n

n

Аналогично, wn 1 w1 ,

wn 2 w2 ,... .

Итак, для любого z 0

корень степени n из числа z имеет n различных значений.

Пример 4.3. Решить уравнение z 3 1 0.

Решение.

Из уравнения имеем z 3

. Найдем модуль и аргумент числа −1:

1

1

1,

arg 1 . Тогда корни уравнения имеют вид:

z 3

3

cos

2 k

i sin

2 k

.

1

cos i sin

y

3

3

Полагая k 0, 1, 2 , получим три корня уравнения:

z0	cos			i sin						1		i			3		,
										2
	3				3								2
z1	cos i sin 1,
			5				5					1								.
z2	cos				i sin								i					3
												2			2
	3				3

	z0
z1	600		x
	1
	z	2
	Рис. 73

Эти корни лежат на единичной окружности иделят ее на три равных части (рис. 73).

Если нужно извлечь корень квадратный, то можно и не пользоваться формулой (4.7). Например,

12i 5 12i 9 4 12i (3i)2 22 (2 3i)2 (2 3i).

Если вы не догадались о таком способе, то можно обозначить 12i 5 x iy и возвести это равенство в квадрат: 12i 5 x iy 2 x 2 2ixy y 2 .

Приравнивая действительные и мнимые части, получим:

	2	y	2		6	2
x				5 x 2			5 x 4 5x 2 36 0.
	2xy				x 2
			12

Действительные корни получившегося биквадратного уравнения x 2. Тогда

y 3 и z x iy (2 3i).

Примеры для самостоятельного решения

Пример. Выполнить указанные действия:

а)

1 i ,

б)

2

, в) 1 i

3 ,

г)

i 6 , д) 3

,

е)

3

3

i

3 4 i.

1 3i

1 i

Указание:

в п. г), д) представить комплексное число в тригонометрической

форме, затем применить формулы (4.6), (4.7).

1 3i

Ответы:

а)

i , б)

,

в) 8 , г)

64 ,

д) 12 3 i ; i, е)

(2- i ).

5

Пример.

Решить квадратные уравнения:

а) z 2 (1 2i)z 2i 0,

б) z 2 (2 i)z 7i 1 0.

Ответы:

а)

2 i ; 1,

б) 3 i, 1 2 i.

40